Интерпретация моделей с распределенным лагом
Эконометрическое моделирование охарактеризованных выше процессов осуществляется с применением моделей, содержащих не только текущие, но и лаговые значения факторных переменных. Эти модели называются моделями с распределенным лагом.Модель вида 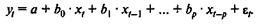 является примером модели с распределенным лагом.
является примером модели с распределенным лагом.
Эта модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной xt то это изменение будет влиять на значения переменной у в течение l следующих моментов времени.
Коэффициент регрессии b0 при переменной xt характеризует среднее абсолютное изменение yt при изменении xt на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.
Вмомент (t + 1) совокупное воздействие факторной переменной xt на результату, составит (bо + b1) усл. ед., в момент (t+2) это воздействие можно охарактеризовать суммой (bо + b1 + b2) и т. д. Полученные таким образом суммы называют промежуточными мультипликаторами.
С учетом конечной величины лага можно сказать, что изменение переменной xt в момент t на 1 усл. ед. приведет к общему изменению результата через / моментов времени на(bо + b1 +...+bl) абсолютных единиц.
Введем следующее обозначение:
bо + b1+...+ bl = b
Величину b называют долгосрочным мультипликатором.Он показывает абсолютное изменение в долгосрочном периоде t + l результата у под влиянием изменения на 1 ед. фактора х.
Предположим
βj = bj/b,j = O:l.)
Назовем полученные величины относительными коэффициентамимодели с распределенным лагом. Если все коэффициенты bj имеют одинаковые знаки, то для любого j
О < βj; < 1 и 
В этом случае относительные коэффициенты βj являются весами для соответствующих коэффициентов bj. Каждый из них измеряет долю общего изменения результативного признака в момент времени (t+j).
Зная величины βj, с помощью стандартных формул можно определить еще две важные характеристики модели множественной регрессии: величину среднего лага и медианного лага. Средний лагопределяется по формуле средней арифметической взвешенной:
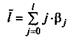
и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, тогда как высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени. Медианный лаг— это величина лага, для которого 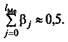
Это тот период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат.
Дата добавления: 2015-08-01; просмотров: 1069;
