Метод отклонений от тренда
Пусть имеются два временных ряда xt и уt каждый из которых содержит трендовую компоненту Τ и случайную компоненту ε. Проведение аналитического выравнивания по каждому из этих рядов позволяет найти параметры соответствующих уравнений трендов и определить расчетные по тренду уровни 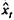 и
и 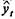 соответственно. Эти расчетные значения можно принять за оценку трендовой компоненты T каждого ряда. Поэтому влияние тенденции можно устранить путем вычитания расчетных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. Дальнейший анализ взаимосвязи рядов проводят с использованием не исходных уровней, а отклонений от тренда
соответственно. Эти расчетные значения можно принять за оценку трендовой компоненты T каждого ряда. Поэтому влияние тенденции можно устранить путем вычитания расчетных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. Дальнейший анализ взаимосвязи рядов проводят с использованием не исходных уровней, а отклонений от тренда 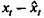 и
и 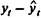 при условии, что последние не содержат тенденции.
при условии, что последние не содержат тенденции.
Содержательная интерпретация параметров полученной модели затруднительна, однако ее можно использовать для прогнозирования. Для этого необходимо определить трендовое значение факторного признака 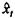 и с помощью одного из методов оценить величину предполагаемого отклонения фактического значения от трендового. Далее по уравнению тренда для результативного признака определяют трендовое значение
и с помощью одного из методов оценить величину предполагаемого отклонения фактического значения от трендового. Далее по уравнению тренда для результативного признака определяют трендовое значение 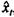 , а по уравнению регрессии по отклонениям от трендов находят величину отклонения
, а по уравнению регрессии по отклонениям от трендов находят величину отклонения 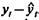 . Затем находят точечный прогноз фактического значения yt по формуле
. Затем находят точечный прогноз фактического значения yt по формуле
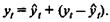
Дата добавления: 2015-08-01; просмотров: 1123;
