Методы исследования кинетики.

Цель исследования – получение достоверного (адекватного) математического описания процесса с учетом истинного механизма смешения и всех факторов, влияющих на процесс.

Существуют 6 методов исследования:

1. Исследование на качественном уровне.

Производится констатацией фактов, и получается оптимальный режим работы смесителя для данного состава. Имеется смесь и аппарат. В результате исследований определяются:

1) возможность приготовления данного состава на данном аппарате;

2) оптимальные параметры смесителя для данного состава;

3) оптимальное время перемешивания.

2. Работа по составлению математической модели на эмпирическом уровне.

Данные в виде регрессионного уравнения не учитывают всех факторов физики процесса и свойств перерабатываемого материала.Исследование производится для определенного класса составов и определенного типа смесителя. Эти формулы описывают конкретный состав для конкретного смесителя; мала адекватность, т.е. большой уровень значимости (большая ошибка в данном уравнении). Для обобщения классов составов эмпирических уравнений необходимо найти зависимость параметров моделей а и в от составов. Тогда этот комплекс уравнений можно применять для данного класса смесей в данной конструкции смесителя для описания кинетики.

3. Кинетика описывается в критериальной форме.

Возможная степень влияния критериев может быть ниже уровня значимости. Поэтому критерии не учитывают всех факторов, а описывают отдельную группу физических факторов. Метод универсален, но не учитывает процесс разложения смеси (сегрегацию). Выводится аналитически критериальное уравнение процесса разложения с последующей экспериментальной проверкой на адекватность. При выводе этого уравнения используется метод анализа размерности и метод подобия. Адекватное уравнение, проверенное на лабораторных аппаратах, можно применять для расчета промышленных аппаратов, при условии сохранения значений критериев постоянными.

4. Описание кинетики на основе опытных данных. Скорость процесса определяется пропорционально самому изменению качества. Недостаток – модели не адекватны в начальных и конечных значениях времени перемешивания.

5. Описание кинетики процесса на основе физических законов. Недостаток – большая неточность. Имеются 3 подхода к выводу уравнения кинетики:

1. предполагает, что механизм смешения состоит из конвективного движения;

2. предполагает, что смешение аналогично процессу диффузии, т.е. чем больше площадь контакта между фазами, тем лучше качество смеси;

3. предполагает смешение как результат сдвиговых деформаций.

Существует множество комбинаций:

- сдвиг и диффузия;

- сдвиг и конвекция;

- конвекция и диффузия.

В основе кинетических уравнений лежат законы физических явлений, таких как:

- теорема действующих масс;

- уравнение неразрывности потока;

- уравнение Фика (I, II).

6. Описание кинетики на основе математических аппаратов цепей Маркова.

Процесс смешения рассматривается как случайный. Модели обладают высокой точностью и в последние десятилетия применяются в полной мере.Стохастическая модель смешения получена после составления структурной схемы с учётом всех моментов возможных состояний системы. Каждое состояние описывается своей моделью с последующим обобщением в единую систему уравнений согласно теории цепей Маркова.

Марковские процессы могут описывать 3 вида систем:

1) дискретные в пространстве и времени;

2) дискретные в пространстве и непрерывные во времени (перемешивание);

3) непрерывное в пространстве и времени.

Марковские процессы имеют свойства:

1) ординарность – определяется кинетическими уравнениями, имеющими один вид для всех перемешанных материалов и устройств. Кинетика процессов неразрывна, т.е. изменение качества смеси происходит непрерывно, без разрыва.

2) Стационарность – моменты распределения однородны для любого времени перемешивания. Независимы от числа испытаний, т.е. при любом испытании с определённой точностью мы воспроизводим кинетическую кривую.

3) Отсутствие после действия – кинетические кривые воспроизводятся с любых точек независимо от начала испытания, только в одну сторону без возврата на предыдущую точку.

Оценка адекватности математической модели:

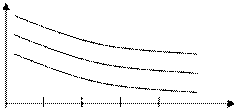
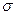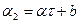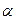
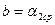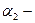1) на качественном уровне оценка производится анализом параметром модели. Для разных значений времени рассчитываются по экспериментальным значениям параметр модели. Методом наименьших квадратов находится зависимость . При этом (или в пределах допускаемого уровня значимости), то , не меняется в процессе (для Марковских систем)

2ая оценка: на количественном уровне (определяется критерием Фишера)

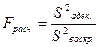
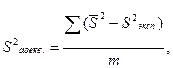где 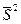– рассчитывается по модели на каждый момент времени.

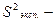экспериментальное количество смеси в те же времена.

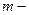число экспериментальных точек.

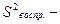дисперсия, значения экспериментальных дисперсий (количество смеси) при 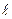параллельных опытах.

S²

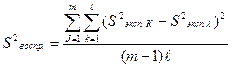
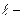число параллельных опытов m – число точек отбора проб

1 2 3 4 t

Находим F_таб с уровнем значимости р=0,05 со степенью свободы по дисперсии адекватности 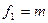и степенью свободы дисперсии воспроизводимости 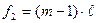и сравнивается .

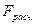Если F_расч.< F_табл. , то модель адекватна.

Если F_расч. > F_табл. , то модель неадекватна, то необходимо определить степень точности модели по уровню значимости выбором табличного значения (F_табл.) большего чем расчётного ( F_расч.), но с другим большим уровнем значимости.