Концептуальный подход

Использование различных концепций в моделировании изнашивания привело к созданию полуэмпирических выражений, которые на протяжении последней четверти века составляют основную расчетную базу для проведения оценок изнашивания. Это связано, во-первых, с достаточной простотой использования полученных зависимостей и, во-вторых, с возможностью качественного и количественного анализа процесса изнашивания. В основу этих моделей, часто построенных на основе физических соображений с учетом теории размерностей, легли следующие предположения:

износ пропорционален пути трения;

износ пропорционален работе силы трения;

износ определяется физическими параметрами процесса и механическими свойствами материалов.

В.Д. Кузнецов под интенсивностью изнашивания J понимал величину износа детали или образца металла, приходящуюся на единицу работы трения:

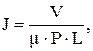(4.27)

где V - износ материала твердого тела за время опыта; m - коэффициент трения; P - нормальная нагрузка; L - путь трения.

Вследствие трудоемкости определения работы силы трения для расчета интенсивности изнашивания выражение (4.27) чаще используют в виде

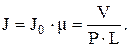(4.28)

Подобный характер имеет и уравнение для расчета изнашивания, полученное Арчардом:

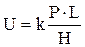, (4.29)

где k - коэффициент изнашивания; Н - твердость.

Полагая, что изнашивание подобно малоцикловой усталости, Чаллен предложил использовать для анализа разрушения эмпирическое уравнение Мэнсона-Коффина и получил выражение для расчета коэффициента изнашивания:

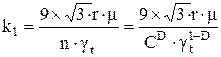, (4.30)

где r - отношение пластической работы к полной работе трения; m - коэффициент трения; n - число циклов до разрушения; С,D - константы материала; g_t - приращение деформации за цикл нагружения.

Д.Г.Эванс и Д.К.Ланкастер предложили новый, более удобный вид уравнения изнашивания Д.Арчарда:

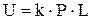, (4.31)

где k - размерный коэффициент изнашивания, обычно записываемый в мм³/Н×м.

Несмотря на столь широкое распространение данной модели практика ее использования указала на некоторые проблемы. В частности, до сих пор отсутствуют достаточно надежные способы оценки коэффициента изнашивания. Влияние различных комбинаций материалов, режимов работы, среды и т.д. часто приводит к большим расхождениям между результатами, полученными расчетным путем, и экспериментальными данными. Кроме того, применявшиеся методы экспериментальной оценки коэффициента изнашивания на стандартном лабораторном оборудовании типа «палец-диск» или «палец-плоскость» не отражают реальные условия работы различных пар трения при эксплуатации.

Наибольшее распространение в России имел подход к разработке модели и расчетных методик изнашивания, предложенный И.В.Крагельским. Его концепция, им же сформулированная, в лаконичной форме звучит следующим образом: износ пропорционален объему взаимного внедрения шероховатостей V_вв.

Эту концепцию иллюстрирует произвольное сечение контакта шероховатых трущихся тел на рис. 4.21.

Строго не рассматривая в деталях эту концепцию, отметим ее блестящую наглядность и убедительность.

В приведенной иллюстрации на рис. 4.21 можно однозначно перечислить, чем определится объем взаимного внедрения: свойства материалов, нагрузка, параметры шероховатости, смазка и др.

В соответствии с этой концепцией И.В. Крагельским предложено базовое уравнение изнашивания, которое пред-полагает усталостный механизм разрушения поверхностей, подобный малоцикловой усталости. Мерой воздействия в его подходе является число циклов нагружения n.

Кратко вывод основного уравнения И.В. Крагельского сводится к следующему.

Вводится понятие удельного износа:

. (4.32)

Здесь i _n - объем изношенного материала при перемещении подвижной детали на расстояние, равное среднему диаметру пятна контакта d, в расчете на единицу ФПК и единицу пройденного пути. Поскольку dV = dh×A_r, то i = dh/d, A_r - ФПК, dh - толщина изношенного слоя при указанном перемещении. При сдвиге на расстояние, равное среднему диаметру пятна, ФПК разрушается и снова восстанавливается. Поэтому на пути скольжения L площадь касания воспроизводится n раз, т.е.

К концу пути изношенный объем составит

DV = dV ^. n . (4.34)

Поскольку интенсивность изнашивания J = DV/LS, то, приняв, что S - площадь трения равна контурной (А_с) или, если волнистость отсутствует, номинальной площади контакта (А_а), можно записать

J = DV/LА_а. (4.35)

Составим отношение J/i с учетом формул (4.33, 4.34 и 4.35):

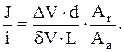
Однако в соответствии с формулами (4.33 и 4.34) DV / dV = L/d = m. Поэтому

J = i (A_r/A_a). (4.36)

Вычислим объем деформированного материала. Из формул (1.15) и (1.16) выразим площадь сечения шероховатого слоя на расстоянии а от верхней его границы (см. рис. 1.3,а):

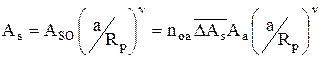. (4.37)

Здесь, как было сказано раньше считается, что А_s=А_а. Деформированный объем материала

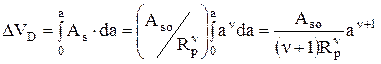. (4.38)

Величина объема, отделившегося вследствие износа за одно нарушение фрикционной связи, составляет

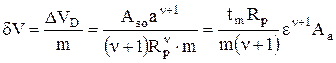. (4.39)

Здесь t_m = A_so/A_a; e = a/R_p; A_r = a A_s. (см. формулы (1.4), (1.10), (1.11)).

Удельный износ

. (4.40)

Среднюю площадь сечения выступа, плоскостью удаленного на а от верхней границы шероховатого слоя, находят, используя формулы (1.5), (1.16), (4.37):

. (4.41)

Если приближенно считать, что 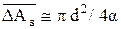, то средний диаметр пятна контакта: 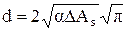. Подставив в это выражение формулу (4.41), получаем

. (4.42)

С учетом (4.40), (4.42) удельный износ

. (4.43)

Интенсивность изнашивания

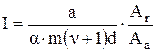. (4.44)

Трудность использования формулы (4.44) заключается в необходимости определения критического числа циклов нагружения, приводящих к разрушению элемента поверхности m. Для этого было предложено использовать закономерность усталостного разрушения при циклическом растяжении. Этот закон описывается формулой Веллера:

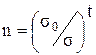, (4.45)

где s₀ - напряжение, приводящее к разрушению при одном цикле нагружения (n=1); s - действующее напряжение; m - число циклов, приводящее к разрушению (разрыву) стержня; t - показатель степени, изменяющийся в зависимости от свойств испытуемого материала в пределах от 3 до 14.

Напряжение связывается с фактическим давлением на контакте и коэффициентом трения соотношением

s = kms_г = kmN/A_г .

Коэффициент k = 3¸5 в зависимости от природы материала.

Несмотря на недостатки, эти модели до сих пор представляют интерес, а методы оценки параметров этих моделей непрерывно развиваются, на что указывает ряд докладов, представленных на Международном трибологическом конгрессе 1997г. в Лондоне.