Процесс разработки и характеристика кинетической модели изнашивания

При разработке модели учитывалось, что в трибологии уже достигнуто понимание основ иерархии процессов деформации и разрушения поверхностей трением. В работе В.И. Владимирова утверждается, что «... адекватную картину пове-

дения материала под внешним воздействием можно получить только из многомасштабных моделей».

Общепризнаны следующие масштабные уровни: микроскопический (атомные и дислокационные размеры), мезоскопический (кооперативные дислокационные эффекты в объемах с размерами сечений 0,1...3,0 мкм), структурный (10^-6 ...10^-3м) и макроуровень, на котором применимы методы теории упругости.

Экспериментальные результаты наших исследований и публикации других авторов свидетельствуют, что основные, наиболее существенные изменения в состоянии материала, деформируемого трением, ведущие к разрушению, происходят на мезоскопическом уровне. К этому уровню относятся микронеровности поверхностей (высотные характеристики), флуктуации полей напряжений при встречах микронеровностей, фрагментированные микрообъемы материала и др.

Сам разрушающийся поверхностный слой материала толщиной ~ 0,1...3,0 мкм тоже, как правило, за исключением грубых форм износа, имеет мезоскопический масштаб. Такой масштабный предел в физике и металловедении связывают с предельно возможной длиной пробега дислокаций.

Учитывая тенденции повышения энергетической напряженности машин (двигателей, конструкций, работающих при интенсивной вибрации, ударах и т.п.), исходили из того, что связь процессов, протекающих на мезоскопическом уровне с макропроцессами, реализуется через деформацию деталей узлов трения (что определяет форму пятна контакта), динамику контактных взаимодействий и локализацию микрообъемов материала, деформируемого трением, связанную с дискретностью контакта шероховатых поверхностей.

При разработке модели использовались представления микромеханики разрушения материалов и математический аппарат кинетической термофлуктуационной теории прочности.

Основные положения предложенной нами модели изнашивания заключаются в следующем.

1. Модель описывает процесс превращения некоторого поверхностного микрообъема материала под действием трения в мелкодисперсные частицы износа. Результирующей характеристикой этого процесса является скорость изнашивания j_v (м³/ч).

2. Конструкция модели подсказана изученным нами феноменом циклического отделения частиц износа при трении, что рассматривалось ранее.

3. Накопление повреждений локализуется в микрообъемах материала, ограниченного площадью SA_r и глубиной h, на которой находится зона наибольшей концентрации дислокаций и других повреждений материала, так называемый debris - слой (рис. 4.22,а). Качественно микрообъем материала, лежащий выше этого

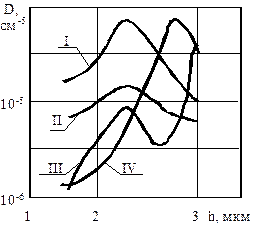
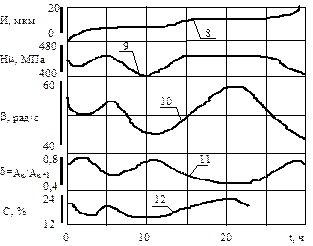
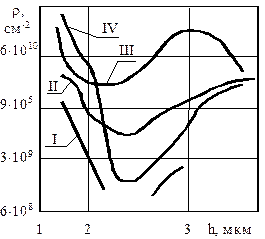
а
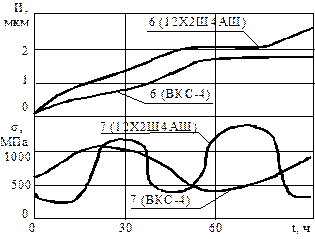
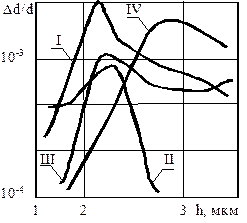
б		в
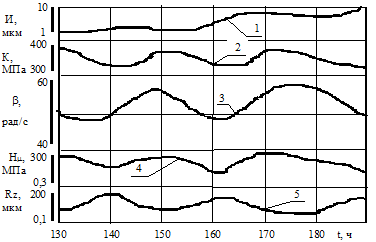
Р и с. 4.22. Циклические изменения состояния материала, деформируемого трением: а - СЧ 21-40; б - конструкционные стали; в - сплав ВТ-9, перестройка состояния материала (сплав ВТ-9) по глубине от поверхности (I,II,III,IV - кривые, соответствующие наработке 10,14,20,26 ч.); г - циклы для сплава никеля (I - износ; 2 - контактная жесткость; 3 - физическое уширение рентгеновских интерференционных линий; 4 - микротвердость; 5 - шероховатость; 6 - износ двух марок стали; 7 - остаточные напряжения ; 8 - износ титанового сплава ВТ-9); 9 - микротвердость на ВТ-9; 10 - физическое уширение интерференционных линий; 11 - демпфирующая способность; 12 - содержание b-фазы; 13 - плотность дислокаций полученная методом ФМР [12]

слоя, характеризуется преобладанием накопления поврежденности над их релаксацией, что обуславливает необратимость его разрушения:

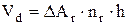. (4.53)

4. Разрушение каждого локализованного микрообъема материала при изнашивании имеет групповой характер и протекает за время охарактеризованного выше кинетического цикла «упрочнение à разупрочнение à разрушение» (рис. 4.22,в).

При этом на первой стадии износ минимален (J à 0), а накопление повреждений носит латентный характер. Длительность этой стадии обычно около 0,7 времени цикла. На второй стадии наблюдается быстрый рост отделения частиц износа. После удаления продуктов износа начинается новый цикл накопления повреждаемости и разрушения на новой совокупности выступающих неровностей.

5. Для описания элементарного акта разрушения использованы представления кинетической термофлуктуационной концепции прочности, в которой долговечность (время существования единичной связи под нагрузкой) определяется известной формулой С.Н. Журкова:

t = t_oexp 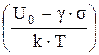, (4.54)

где t₀ - постоянная времени; U₀ - энергия активации разрушения межатомной связи при отсутствии внешних напряжений; g - структурно-чувствительный коэффициент; k - постоянная Больцмана; Т и s - абсолютная температура и напряжение.

6. Общее число связей l, разрушающихся в каждом микрообъеме материала V_d за один кинетический цикл, оценивается гипотетически с помощью ряда принятых упрощений. Так, форма частиц износа (рис.4.22,б) условно принята сферической. Такую же форму имеет элементарный активационный объем V_a. Число разрушаемых связей определяется по количеству межузлий единичной кристаллической решетки N_p с учетом отношения локализованного микрообъема материала V_d к объему среднестатистической частицы V_кр и отношения поверхности частицы среднестатистического размера S_Vкр к поверхности одного активационного объема Sv_a:

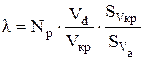_· (4.55)

7. Общее время одного цикла t, необходимое для разрушения микрообъема материала V_d, определяется на основе гипотезы линейного суммирования повреждаемости, при уточнении количественной стороны по экспериментальным данным (см. рис.4.22,в).

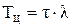. (4.56)

8. Изнашивание в расчетной модели измеряется средней скоростью диспергирования локализованного поверхностного микрообъема материала, м³/ч, за время цикла:

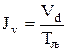. (4.57)

С учетом требований размерности, характеристики релаксации повреждений П_р, исходной повреждаемости материала x, а также диссипативности контакта (коэффициент поглощения y) соотношение (4.57) как базовое уравнение изнашивания представлено в виде

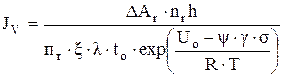. (4.58)

Уравнение (4.58) является базовым для построения расчетных схем и методик прогнозирования скорости изнашивания конкретных триботехнических задач.

Приведем пример, в котором уравнение (4.58) было использовано для расчета изнашивания шлицшарнира основной стойки шасси самолета ТУ-134.

На рис. 4.22,г приведены результаты расчета, данные стендовых испытаний и эксплуатации шлицшарнира. Максимальная расчетная нагрузка в режиме пробега по взлетной полосе составляет 20,0 МПа, коэффициент динамичности - 1,7.

Разброс данных износа в эксплуатации по ряду аэропортов - поле между кривыми 1 - - 1¹ - связан с климатическими зонами и производственной культурой эксплуатации. Наибольший износ имели шарниры шасси самолетов северных линий, наименьшее - в аэропорту г. Рига.

Стендовые эквивалентные испытания (рис. 4.22,г) имеют существенно меньший разброс, что связанно с исключением влияния эксплуатационных факторов (области рассеяния заштрихована).

Расчетная кривая 3 (полученная для режима оптимальной эксплуатации) приближается к данным из благоприятных авиапредприятий.

Предлагаемая методика расчета позволяет прогнозировать не только среднюю ожидаемую величину износа, но и его распределение по пятну контакта (см. рис.4.22,д).

При расчете изнашивания с интенсивными окислительными превращениями на поверхностях, когда разрушается не сам материал, а его вторичные структуры, например при фреттинг-коррозии, в формулу (4.58) необходимо вводить поправку К_кор для структурно-чувствительного коэффициента g:

g _кор = g × К _кор. (4.59)

Значение этой поправки зависит от концентрации кислорода С, поступающего в зону контакта. Концентрация кислорода по А.К. Дедкову уменьшается при удалении от кромки зазора:

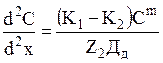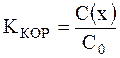; , (4.60)

где C (x) - находят из решения уравнения (4.60).

Гидродинамические эффекты при трении со смазочным материалом можно учитывать в соответствии с методологией Ю.Н. Дроздова. Используя общепринятые в контактной гидродинамике критерии подобия, влияние гидродинамики учитывали через коэффициент гидродинамического влияния К_гидр:

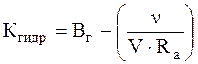, (4.61)

где В_г - эмпирический коэффициент; n - вязкость; V- скорость скольжения; R_a - высота шероховатостей.

Для учета теплового влияния на скорость изнашивания в уравнение (4.58) потребовалось внести поправку. Численное исследование уравнения в широком диапазоне температур (270...1000⁰К) показало, что с ростом температуры после 400К имеет место существенное отклонение расчетной скорости изнашивания от наблюдаемых значений.

Это связано с тем, что Больцманов множитель A exp 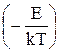, используемый в нашей модели, не может количественно характеризовать тепловые процессы в связи с высокой сложностью трибосистемы. Поэтому поправочный параметр К_т, устраняющий имеющиеся расхождения, был определен эмпирическим путем и представлен в виде степенной функции

К_т » A_т × Т^3/4, (4.62)

где А_т » 0,011.

Последний комментарий к формируемой модели касается определения действующего напряжения s.

Для этой цели были рассмотрены связи между подсистемами 2, 3, 5 и 6, приведенные в табл. 4.4.

Действующие на площадках фактического контакта напряжения включали в себя статическую компо­ненту s_ст (например, определяемую натягом или массой элементов конструкции), динамическую компоненту s_дин, определяемую инерционными процессами (макродвижение, вибрации, удары) и волны напряжений s_волн, генерируемые рабочим процессом и самим трением.

Как принято в расчетах деталей машин, динамические приращения контактных напряжений представляют с помощью коэффициентов динамичности:

s_{действ.} = s_стат. × К_вибр. × К _волн. . (4.63)

По нашей оценке (например, для шасси) можно принимать средние значения К_вибр » 1,20...1,35, а К _волн » 1,1...1,25.

Заключение

Если сравнить первую кинетическую модель изнашивания, предложенную С.Б. Ратнером, с тем, что представлено выше, то можно отметить следующее.

Во-первых, модель С.Б. Ратнера как бы переносит закономерность разрушения элементарной связи, описанной экспоненциальной функцией Больцмана, на макрообъем. Такое решение обосновать трудно.

В новой модели учтен масштабный фактор. Единичные связи (пучки связей) разрушаются на микроуровне (в пределах единичного активационного объема материалов), а частицы износа, которые принадлежат к мезоскопическому уровню, образуются при разрушении связей на их потенциальных (ожидаемых) поверхностях, как правило, по границам зерен материала. Величина же обычного износа (макроуровень) складывается из множества отделяющихся частиц.

Во-вторых, как это можно увидеть по изложенному выше, в модели учтен не только основной механизм разрушения, но и ряд наиболее существенных факторов, определяющих ход изнашивания: дискретность контакта, локализованный микрообъем материала, динамика контактной нагрузки, вклад химических превращений и др. Такие схемы не содержит ни одно из известных уравнений изнашивания.

Применение предложенного уравнения для расчетных целей в контактных случаях может потребовать учета дополнительных обстоятельств, подобных приведенным примерам, но они могут быть реализованы расчетными методами.

Методика расчетов изнашивания (её общая схема) состоит в том, что последовательно выполняют следующие операции:

определяют нагрузку, действующую на узел трения;

определяют деформацию узла трения при действии этой нагрузки, площадь, форму пятна контакта и величину действующих контактных напряжений (для их определения используется метод объемных конечных элементов и соответствующее программное обеспечение);

на каждом из элементов разбиения площади контакта определяют фактическую площадь контакта A_r и фактическое давление Р_r, изменяющиеся в зависимости от режима работы узлов трения, например, для авиационных изделий: запуск, прогрев, режим руления, взлет, набор высоты, крейсерский режим, посадка, торможение и т.п.

Изнашивание на каждой площадке разбиения J_t = j(s_кi), определяется с учетом этих режимов и их продолжительности согласно выражению (4.59).

При подобных уточнениях результаты расчетов дают неплохое совпадение прогноза и реального изнашивания.

В заключение отметим, что наиболее существенным во всей приведенной разработке, по нашему мнению, является то, что кинетический подход к моделированию изнашивания позволяет в удобной математической форме учитывать разнородные процессы различной природы (механические, химические, тепловые, акустические и др.), имеющие место при трении и разрушении поверхностей.

[1] В настоящей главе использованы примеры из книги "Триботехника" проф. Д.Н. Гаркунова.