Оценка долговечности узлов трения методами теории вероятности
Долговечность узла трения - это время работы с заданной надежностью. Надежность выражается, как вероятность безотказной работы:
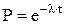 , (5.38)
, (5.38)
где t - время работы; 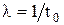 - интенсивность отказов; t0 - средняя продол-жительность безотказной работы (средний промежуток времени между двумя отказами).
- интенсивность отказов; t0 - средняя продол-жительность безотказной работы (средний промежуток времени между двумя отказами).
Из рис. 5.54 видно, что чем выше интенсивность отказов, тем меньше долговечность при заданном уровне надежности (D2 <D1).
При работе сложных систем, состоящих из множества элементов (узлов), к которым относятся автотранспортные средства, надежность системы
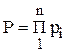 , (5.39)
, (5.39)
где pi - надежность i-того узла; n - число узлов. Чем сложнее система, тем ниже ее надежность.
Основным путем повышения надежности узлов трения является повышение износостойкости. Ограничением является стоимость мероприятий по повышению износостойкости, что мотивирует выбор общего ресурса автомобиля.
У легковых автомобилей принят ресурс в размере 5, у грузовых - 10 лет при уровне надежности порядка 0,9. Часто долговечность выражают в виде пробега в тысячах километров, подразумевая, что за этой дистанцией скрывается время без-
| аварийного движения с некоторой средней скоростью, например в 60 км/ч. По величине этой дистанции в первом приближении и можно судить о качестве автотранспортного средства. Вероятность безотказной работы узла трения (и любого другого механизма) означает, что в пределах заданного промежутка времени эксплуатации отказ невозможен. Он наступает в результате достижения предельного износа и проявляется, например, в поломке зубьев шестерен; заклинивании деталей газораспределительного механизма; проскакивании цепи в цепной передаче в результате износа втулок, | ||
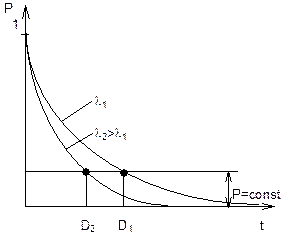
| ||
| Р и с. 5.54. Кривые надежности | ||
роликов и зубьев звездочек; заклинивании подшипников качения и скольжения; разрушении шарниров рулевого управления и подвески; накладок и колодок муфт сцепления и тормозов и т.д. Обычно для каждого механизма из сведений по эксплуатации известна предельно допустимая величина линейного износа Dhпр. Например, для пары вал-втулка подшипника скольжения, Dhпр=h-h0, где h0, h - значения начального и текущего зазоров в сопряжении. Однако за расчетную предельную величину износа принимают 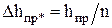 , где n - коэффициент запаса.
, где n - коэффициент запаса.
Условие безотказной работы
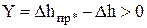 , (5.40)
, (5.40)
где Dh - текущее значение износа.
Входящие в это неравенство величины являются случайными. Обычно считают, что все они распределены по нормальному закону:
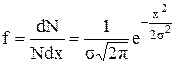 . (5.41)
. (5.41)
Здесь под х понимают величину износа  , где
, где 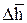 - среднее арифметическое значение
- среднее арифметическое значение 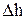 0. Для достаточно большого числа испытаний (N>50)
0. Для достаточно большого числа испытаний (N>50)
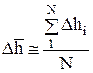 . (5.42)
. (5.42)
Среднее квадратичное отклонение
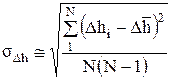 (5.43)
(5.43)
Для системы случайных величин,
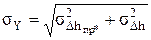 . (5.44)
. (5.44)
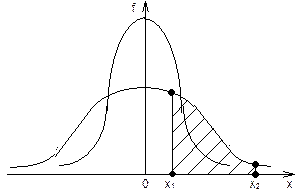
На рис. 5.55 представлен вид кривых нормального распределения. Площадь, ограниченная кривой и осью абсцисс, равна 1, т.е.
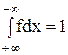 .
Чем больше среднее квадратичное отклонение, тем более полно идет кривая. Заштрихованная площадь равна вероятности того, что .
Чем больше среднее квадратичное отклонение, тем более полно идет кривая. Заштрихованная площадь равна вероятности того, что 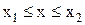 . Для нор-мального закона, если . Для нор-мального закона, если 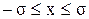 , , 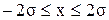 , , 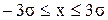 , вероятнос-ти соответственно составляют 0,68; 0,95; 0,99. , вероятнос-ти соответственно составляют 0,68; 0,95; 0,99.
| ||
| ||
| Р и с. 5.55. Кривые нормального распределения | ||
Таким образом, вероятность реализации соотношения (5.39), т. е. безотказной работы,
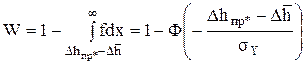 . (5.45)
. (5.45)
Величина, стоящая в скобках, - квантиль нормального распределения. Отношение среднего квадратического отклонения к среднеарифметической величине называется коэффициентом вариации и характеризует относительную точность определения износа. Для предельного значения и произвольной величины износа коэффициенты вариации
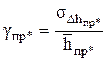 ;
; 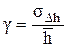 . (5.46)
. (5.46)
Средний интегральный износ
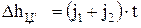 , (5.47)
, (5.47)
где j1,2 - скорости изнашивания первого и второго элементов пары трения. Соотношение (5.46) справедливо для изнашивания с постоянной скоростью. Для периода приработки, когда скорость изнашивания меняется с течением времени, для расчета износа можно воспользоваться соотношениями, приведенными в главе "Изнашивание".
В качестве критерия долговечности используется ресурс – время, в течение которого достигается предельное состояние узла либо машины в целом с заданной вероятностью W=g (гамма-процентный ресурс). В технике, в частности для автомобилей, принимают g=0,9 (90%). Ресурсные испытания проводятся предприятиями-изготовителями или специальными НИИ по 20000, 50000-часовым программам. Ресурс (Тg) - случайная величина, распределенная по некоторому закону. Часто используется нормальный закон. Однако в последнее время стали предлагаться и другие законы распределения, которые, как считают некоторые специалисты, более точно описывают результаты испытаний. Таким образом, обрабатывая результаты испытаний, приняв гипотезу о законе, который описывает распределение ресурса, определяют гамма-процентный ресурс. Поскольку испытания имеют затяжной характер и требуют больших материальных затрат, иногда используют методы ускоренных испытаний, ужесточая режим. Результаты пересчитываются на реальные объекты с использованием методов теории подобия. Такой подход требует постановки небольшой серии поверочных испытаний.
Поскольку испытания являются важнейшим инструментом в руках конструктора, применение статистических методов имеет важнейшее значение для обеспечения корректности и достоверности оценки параметров надежности узлов трения.
Дата добавления: 2015-07-06; просмотров: 1475;
