Разработка и теоретическое обоснование нового способа оценки активационных параметров материалов при склерометрировании
Как уже отмечалось, с точки зрения термодинамики, поверхностный слой является сложной системой. Уникальность ее состоит в том, что поверхностный слой обладает как свойствами объемного твердого тела, с присущими ему структурой, составом, плотностью, твердостью и т.д., так и свойствами мембраны, являясь посредником между внешней средой и нижележащими слоями тела. Кроме того, поверхностный слой является открытой системой, что обусловлено его способностью пропускать и обменивать через границы раздела энергию и вещество. Как мембрана, поверхностный слой передает через себя тепловые, механические и другие воздействия, испытываемые телом извне, из среды вглубь материала и наоборот. Вместе с тем, как объемное твердое тело, поверхностный слой способен запасать в себе некоторую часть пропускаемой им энергии в виде тепла и микродефектов, что приводит к образованию специфических диссипативных структур.
Одной из важнейших функций состояния термодинамической системы является внутренняя энергия. Эта функция аддитивна; ее величина определяется суммой энергий, сосредоточенных в массе, а также в излучении вещества системы. В поверхностном слое, не затрагивая уровни ниже атомарного, эта энергия включает потенциальную энергию межатомных взаимодействий, кинетическую (тепловую) энергию атомов, энергию дефектов кристаллической решетки, а также свободную энергию, обусловленную несовершенством кристаллической решетки на границе «металл-среда».
Каждая система стремится к некоторому устойчивому в данных условиях состоянию. Несмотря на то, что любой процесс, в котором участвует система, вызывает изменение ее внутренней энергии, это изменение чаще всего носит компенсирующий характер. Так, например, при упругих деформациях тело запасает такое количество внутренней энергии, которое ему необходимо, чтобы совершить работу по восстановлению исходной формы. Наиболее устойчивым состоянием системы является такое, при котором ее свободная энергия становится минимальной. По этой причине в термодинамических системах происходит самопроизвольная активация механизмов, которые при данных условиях наиболее эффективно понижают внутреннюю энергию системы. К таким механизмам можно отнести упругое восстановление формы кристаллической решетки после снятия внешних деформирующих напряжений, теплоотвод, выход дефектов из кристаллической решетки, адсорбцию и хемосорбцию частиц среды свободной поверхностью. В зависимости от внешних условий эти процессы протекают самопроизвольно с различными скоростями. Так, например, при трении поверхность практически мгновенно покрывается различными пленками, которые в определенной мере компенсируют избыток свободной энергии металла.
Однако не всегда система может реагировать на внешние процессы обратимо. Существуют определенные пороговые значения внутренней энергии, в которых система теряет устойчивость, и ее самопроизвольный возврат в прежнее состояние становится невозможен. Точка на диаграмме состояния материала, в которой устойчивое состояние сменяется неустойчивым, называется точкой бифуркации, а процесс, сопровождающийся переходом системы через точку бифуркации, называется кинетическим. К ним можно отнести пластическую деформацию, хемосорбцию, диффузию и другие процессы, в ходе которых образуются новые устойчивые образования, формы или соединения. Высота энергетического барьера, численно равная разности между внутренней энергией системы в исходном и неустойчивом (активированном) состояниях, и является энергией активации этих процессов.
Изнашивание материалов при трении схематично можно представить в виде последовательности «устойчивость (I) - неустойчивость (II) - устойчивость (III)» (рис. 3.15). В этом случае значение энергии активации разрушения поверхностного слоя при трении равна разности внутренней энергии системы в исходном (I) и активированном (II) состояниях.

| 
| |
| а | б | |
| Р и с. 3.15. Энергетическая диаграмма кинетических переходов (I) – устойчивость, - неустойчивость (II) - устойчивость (III): d - среднее межатомное расстояние; d’ - межатомное расстояние под действием внешней нагрузки; l - параметр повреждаемости; U0 - энергия активации процесса; U(s) - эффективная энергия активации; Uе - запасенная энергия решетки; g.s - механическая работа по растяжению межатомной связи | ||
Существует несколько подходов к физической интерпретации понятия энергии активации. Первый, предложенный Р.Беккером, рассматривает ее как обратимую изотермическую работу, которую необходимо затратить для активации исследуемого процесса. Второй подход, использованный В.Кауцманом и Г.Эйрингом, основан на теории абсолютных скоростей реакций, согласно которой энергия активации равна необратимому изменению изобарно-изотермического потенциала системы. Однако современный уровень знаний об иерархии и эволюции диссипативных процессов в деформируемом материале позволяет утверждать обоснованность обоих подходов, но применительно к соответствующим масштабным уровням.
Единичный акт разрушения межатомной связи согласно термофлуктуационой теории происходит за счет суммарной энергии механического отклонения частиц от положения равновесия и энергии термической флуктуации (см. рис. 3.15,а). Если энергии термической флуктуации окажется недостаточно, чтобы преодолеть потенциальный барьер U0, частица вернется в исходное положение. Следовательно, работа по растяжению межатомной связи между состояниями (I), (II) совершается упруго, т.е. обратимо. Согласно теории точечных дефектов Зинера данная работа совершается изотермически. Таким образом, для оценки появления единичных актов повреждения на микроуровне пригоден подход Р.Беккера.
Переходя к мезо- и макроуровням, необходимо отметить, что процесс пластической деформации сопровождается необратимым накоплением повреждений в материале (увеличение плотности дислокаций). При этом совершаемая механическая работа деформации единицы объема будет равна увеличению изобарно-изотермического (термодинамического) потенциала системы при появлении единичной дислокации в единице объема. Поскольку дислокации при пластической деформации накапливаются в объеме, то повышение внутренней энергии системы, обусловленное упругими искажениями кристаллической решетки, будет пропорционально увеличению их плотности (см. рис. 3.15,б). Следовательно, на мезо- и макроуровнях применим подход В.Кауцмана и Г.Эйринга. Данный подход, объясняющий возможность потери устойчивости системы на макроуровне за счет постепенного накопления повреждений, является физически обоснованным, поскольку возбужденное состояние не может быть обеспечено однократным появлением термической флуктуации в материале, находящемся в исходном состоянии. С другой стороны, при этом реализуется термоактивационный механизм разрушения, так как в состоянии предразрушения (вблизи точки бифуркации системы) появление единичного повреждения за счет термических флуктуаций способно вызвать неустойчивость всей макросистемы.
Третий подход, объединяющий первые два, состоит в том, что энергия активации оценивается как повышение внутренней энергии мезо- (или макро-) системы за счет суммарной работы, затраченной на упругое смещение частиц материала от положения равновесия, понижающее энергию образования единичных повреждений, и на необратимый рост числа дислокаций в плоскостях скольжения до величины, при которой активируется сдвиг решетки по данной плоскости, т.е. пластическая деформация материала. Этот подход является наиболее справедливым для описания синергетических процессов на стадии сосредоточенных деформаций
(предразрушения), когда основная роль в диссипации энергии трения отводится дислокационным субструктурам (блокам, фрагментам), которые являются объектами мезоскопического уровня.
Рассматривая трибологические процессы, можно также отметить три стадии развития усталости в материале. Исходное состояние (I) соответствует приработанному в заданных условиях материалу поверхностного слоя. Возбужденное состояние (II) соответствует точке бифуркации, в которой материал теряет устойчивость. Чтобы вызвать это состояние необходимо передать материалу часть энергии для активации механизмов, приводящих к его разрушению. На заключительной стадии (III) материал приобретает новое устойчивое состояние, соответствующее завершению кинетического цикла. Процессы деформации и разрушения завершаются оттеснением (либо удалением) активированного вещества из зоны действия напряжений.
Как ранее было отмечено, деформация и разрушение металлических материалов могут быть вызваны различными механизмами, действующими на микроуровне (рис. 3.16). Активация того или иного механизма определяется совокупностью значений внешних факторов, действующих на материал. Наиболее существенное влияние на прочность материалов оказывают напряжения, температура, а также химическая активность рабочих сред. При эксплуатации металлических изделий скорость их деформации и разрушения контролируется теми величинами U0 и g, которые соответствуют доминирующему в данных условиях механизму.
 В гл.1 было показано, что нагрузки в зонах фактического контакта трущихся поверхностей превышают предел текучести. Но известно, что процесс накопления повреждений в поверхностном слое при циклических нагрузках, превышающих предел текучести, подобен малоцикловой усталости. Малоцикловая усталость поверхностного слоя является основной причиной его разрушения при наиболее распространенных видах механического и коррозионно-механического изнашивания: усталостного, абразивного, фреттинг-корррозии и др.
В гл.1 было показано, что нагрузки в зонах фактического контакта трущихся поверхностей превышают предел текучести. Но известно, что процесс накопления повреждений в поверхностном слое при циклических нагрузках, превышающих предел текучести, подобен малоцикловой усталости. Малоцикловая усталость поверхностного слоя является основной причиной его разрушения при наиболее распространенных видах механического и коррозионно-механического изнашивания: усталостного, абразивного, фреттинг-корррозии и др.
В условиях высоких напряжений и умеренных температур, не превышающих 0,5Тпл, деформация материалов преимущественно обусловлена действием механизма скольжения дислокаций. В отличие от механизма ползучести, скольжение дислокаций может происходить с высокими скоростями, соизмеримыми со скоростью звука в металле. Пластическая деформация получила название мгновенной, поскольку релаксация наступает практически за время существования деформирующих напряжений. Однако это справедливо лишь в том случае, когда действующие напряжения близки к значению истинной прочности материала на разрыв. В более общем случае, когда действующие напряжения превышают предел текучести материала, но не достигают разрывного напряжения, процессы пластической деформации и разрушения материалов являются термоактивируемыми и происходят со скоростями меньшими, чем скорость звука. При этом скорость образования и скольжения дислокаций определяются не только интенсивностью деформации, но и температурой материала, наличием в нем дефектов, создающих локальные, препятствия для подвижных дислокаций и другими факторами.
Специфика оценки энергии активации разрушения U0 и структурно-чувствительного коэффициента g в поверхностных слоях, модифицированных трением, состоит в следующем.
1. Реальный материал поверхностного слоя после приработки сохраняет кристаллическое строение, но в результате физико-химической модификации он насыщается всеми видами дефектов. Неоднородность и анизотропия материала поверхностного слоя не позволяют использовать для его описания классические теории (упругости, пластичности и др.). Поэтому оценить активационные характеристики при помощи известных теоретических методов не представляется возможным. Единственным источником данных в этом случае остается эксперимент.
2. Накопление повреждений при трении происходит в поверхностном слое определенной толщины, так называемом debris-слое. Наиболее характерная глубина debris-слоя имеет мезоскопические размеры порядка 1-3мкм. Следовательно, масштабный уровень эксперимента должен быть достаточно большим, чтобы полученные оценки отражали общее, усредненное состояние модифицированного материала поверхностного слоя, но и достаточно малым, чтобы не выйти за пределы изучаемого слоя.
3. При исследовании активационных характеристик была установлена их зависимость от создаваемого при испытаниях схемы напряженно деформированного состояния. При трении создается сложное напряженно-деформированное состояние материала поверхностного слоя при действии нормальных и касательных нагрузок, упругих и пластических деформаций выступов контактирующих тел. Следовательно, эксперименты должны выполняться при напряженно-деформированном состоянии, адекватном тому, которое создается в зоне контакта при реальном трении.
4. В результате многократной пластической деформации поверхностного слоя при трении металлические зерна вытягиваются в направлении трения и образуется специфическая текстура поверхностного слоя (вторичная анизотропия). При этом деформационные и прочностные характеристики материала начинают изменяться в зависимости от направления действия внешних нагрузок. Поэтому при испытаниях необходимо прилагать нагрузки к образцу в том же направлении, в котором они действовали при трении.
5. Энергия активации U0 и структурно-чувствительный коэффициент g зависят от действующего микромеханизма повреждения. Как было отмечено, при трении доминирующим механизмом является образование и скольжение дислокаций. Следовательно, при испытаниях необходимо создать условия для активации этого механизма.
В связи с отмеченным расчетную модель энергии активации на основании теории С.Н.Журкова можно представить в виде
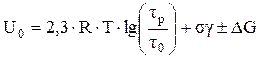 . (3.23)
. (3.23)
Число слагаемых в правой части равно числу основных факторов разрушения поверхностного слоя. Первое слагаемое - термическое. Оно содержит часть внутренней энергии системы, составляемую тепловыми колебаниями атомов в узлах кристаллической решетки. Второе слагаемое - механическое, является частью внутренней энергии, поставляемой в систему за счет упругого искажения кристаллической решетки от внешних механических воздействий. Оно также включает часть механической энергии, затраченной на образование дефектов и перешедшей при трении в энергию упругих искажений кристаллической решетки поверхностного слоя. Третье слагаемое представлено в виде обобщенного параметра DG, имеющего химическую природу. Он отражает суммарный эффект, производимый физико-химическим взаимодействием поверхностного слоя со средой. В условиях инертной среды можно принять DG @ 0. Оценку энергии активации разрушения производят путем возбуждения этого процесса в испытуемом материале при помощи одного или нескольких разрушающих факторов. По экспериментальным данным рассчитываются величина слагаемых данной модели и собственно энергия активации разрушения.
Величина энергии активации в существенной мере зависит от природы действующего механизма разрушения. Поэтому каждый материал имеет столько значений энергий активации разрушения, сколько существует механизмов этого процесса. Как отмечалось, потерю устойчивости и, как следствие, деформацию или разрушение материалов могут вызвать три основных фактора: термический, механический и химический. Все они, в общем случае, воздействуют на материал одновременно, но не в равной степени. В реальности достаточно выделить и рассматривать только один механизм разрушения, который при данных условиях является ведущим. Этот механизм должен иметь наименьшую величину энергии активации. В большинстве практических случаев таким механизмом при трении является сдвиг кристаллической решетки материала поверхностного слоя в зонах фактического контакта, который обусловливает пластическую деформацию поверхностного слоя и малоцикловую усталость, что в конечном счете приводит к его разрушению. Отличительной особенностью данного механизма разрушения является то, что он проявляется при достаточно высоких внешних напряжениях и сохраняет устойчивость вплоть до появления атермических разрывов межатомных связей. Это позволяет применить для оценки энергии активации разрушения поверхностного слоя при пластической деформации метод механической активации.
Оценка активационных параметров разрушения при механической активации материала может выполняться лишь при условии, что действующие при испытаниях нагрузки близки к истинной прочности материала на разрыв (при растяжении) или твердости (при сжатии). В этом случае можно принять, что 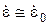 и
и 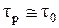 . Это допущение оправдано тем, что при действии максимальных для данного материала нагрузок скорость деформации и время до разрушения принимают также максимальные значения. Поэтому такие нагрузки способны вызвать практически мгновенную потерю устойчивости (разрыв, деформацию) испытываемого образца. При указанных допущениях первое слагаемое в выражении (3.23) становится пренебрежимо малым, так как отношение tр к t0 приближается к единице. Таким образом, в этом случае процесс можно рассматривать как атермический. Поскольку первое слагаемое при указанных условиях обращается в нуль, можно исключить из анализа фактор времени, что придает испытаниям экспрессный характер. Механический способ активации опирается на следующее обоснование. Как отмечалось выше, второе слагаемое, согласно термофлуктуационной концепции, имеет механическую природу. Известно, что механическая энергия, затраченная на активацию какого-либо процесса, имеет смысл механической работы А, которая может определяться как работа напряжений или работа сил:
. Это допущение оправдано тем, что при действии максимальных для данного материала нагрузок скорость деформации и время до разрушения принимают также максимальные значения. Поэтому такие нагрузки способны вызвать практически мгновенную потерю устойчивости (разрыв, деформацию) испытываемого образца. При указанных допущениях первое слагаемое в выражении (3.23) становится пренебрежимо малым, так как отношение tр к t0 приближается к единице. Таким образом, в этом случае процесс можно рассматривать как атермический. Поскольку первое слагаемое при указанных условиях обращается в нуль, можно исключить из анализа фактор времени, что придает испытаниям экспрессный характер. Механический способ активации опирается на следующее обоснование. Как отмечалось выше, второе слагаемое, согласно термофлуктуационной концепции, имеет механическую природу. Известно, что механическая энергия, затраченная на активацию какого-либо процесса, имеет смысл механической работы А, которая может определяться как работа напряжений или работа сил:
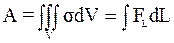 . (3.24)
. (3.24)
При механическом возбуждении энергию активации можно интерпретировать как работу напряжений, затраченную на пластическое оттеснение элементарного объема dV, или работу сил по перемещению частиц материала на элементарном пути dL. Второе определение является более удобным, так как экспериментальная оценка параметров FL и L производится проще, чем s и V.
Поскольку механический способ активации деформации и разрушения поверхностного слоя позволяет производить воздействие на исследуемый материал в любом направлении и на любом выбранном участке поверхности, а также активировать процесс малоцикловой усталости за счет многократного повторения деформирующих воздействий, этот способ отвечает требованиям объективности при воссоздании процессов, имеющих место при трении, и является оптимальным для изучения активационных характеристик материала поверхностного слоя. Разработка такой методики выполнена в Самарском техническом университете в 1995 - 1998 гг. Д.Г. Громаковским, И.Д. Ибатуллиным и А.Г. Ковшовым.
Для оценки механических свойств поверхностного слоя чаще всего применяются методы пенетрации (вдавливания) и склерометрии (царапания) поверхности твердыми инденторами. Принципиальное различие этих двух методов состоит в схеме приложения нагрузок: в первом случае нагружение происходит только в нормальном направлении, во втором - индентор воздействует на поверхностный слой в нормальном и касательном направлениях. Второй случай более близок к процессу деформации, происходящему при реальном трении, поэтому он представляется наиболее целесообразным при трибологических исследованиях поверхностного слоя.
Метод склерометрии заключается в том, что в исследуемую поверхность под воздействием нормальной нагрузки внедряют индентор, затем, приложив тангенциальное усилие, осуществляют относительное перемещение индентора, в результате чего образуется канавка с металлом, оттесненным на ее края за счет сдвига. Размеры канавки используются для оценки механических характеристик материала. Инденторы для этих целей изготавливаются из твердых материалов (монокристаллы сапфира, алмаза), как правило, в форме правильной пирамиды или конуса.
Царапание по ГОСТ 16429-70 определяется как процесс образования углублений на поверхности в направлении скольжения под воздействием выступов твердого тела или частиц. Царапание может осуществляться в разных режимах: микрорезания, пластического оттеснения материала и образования выступа перед индентором. Влияние различных факторов на режимы царапания показаны на рис. 3.17.
Метод склерометрии широко известен и применяется в трибологии уже достаточно долгое время. В числе первых исследователей этого метода были Д.Тейбор, В.Д.Кузнецов, И.В.Крагельский, Н.Н.Давиденков, М.М.Хрущев и др. Данный метод имеет многоцелевой характер, и поэтому в настоящее время он находит применение во многих странах при решении широкого спектра задач.
 Кроме адекватности напряженно-деформированного состояния при царапании и контактном взаимодействии выступов трущихся поверхностей, применение метода склерометрии можно обосновать следующим:
Кроме адекватности напряженно-деформированного состояния при царапании и контактном взаимодействии выступов трущихся поверхностей, применение метода склерометрии можно обосновать следующим:
царапание позволяет произвести деформацию материала поверхностного слоя на необходимой глубине в зависимости от приложенной нормальной нагрузки;
высокие контактные нагрузки pr@Нm при царапании обеспечивают условие, необходимое для активации дислокационного механизма повреждения поверхностного слоя, наиболее часто наблюдаем при пластическом деформировании;
выбор направления царапания позволяет выявить анизотропию свойств материала поверхностного слоя;
возможность осуществления повторных проходов индентора по одному участку поверхности позволяет оценить свойства изучаемого материала при накоплении повреждений в режиме малоцикловой усталости.
При изучении материала модифицированного поверхностного слоя необходимо учитывать, что он включает структурные элементы различного масштаба: атомы, нуль- и одномерные дефекты - на микроуровне; дислокационные ячейки, клубки, зерна - на мезоуровне; топографию и зеренную структуру - на макроуровне. Воздействие индентора вызывает пластическую деформацию поверхностного слоя на микро- и мезоуровнях. Объективность оценки активационных характеристик достигается при условии, что деформируемая область включает множество различных структурных элементов, что позволяет при выполнении эксперимента усреднить влияние всех действующих механизмов. Это соответствует структурно-феноменологическому подходу, при котором энергия активации может быть рассмотрена как полная энергия, затраченная на активацию совокупности всех механизмов повреждения, которые на мезо- и макроуровнях вызывают пластическую неустойчивость и оттеснение вещества поверхностного слоя количеством в один моль. При этом совокупность действующих механизмов полагается заранее неизвестной и представляется в виде «черного ящика». Оценке подлежат только входные параметры в виде затрачиваемой механической энергии и выходные в виде результирующего количества оттесненного вещества.
Для реализации способа склерометрии существуют специальные приборы - склерометры, исполнение которых, в зависимости от цели проводимых исследований, может быть весьма многообразным. В настоящее время отсутствует стандартное оборудование для склерометрических испытаний. Однако для оценки энергии активации разрушения поверхностного слоя можно воспользоваться стандартным микротвердомером ПМТ-3. Царапание осуществляется за счет горизонтального перемещения столика с закрепленным образцом относительно неподвижного индентора, опущенного на поверхность образца (рис. 3.18, 3.19). Нагружение индентора производится при помощи стандартных навесок массой 2¸200 г. Размеры борозды определяются при помощи оптического микрометра.
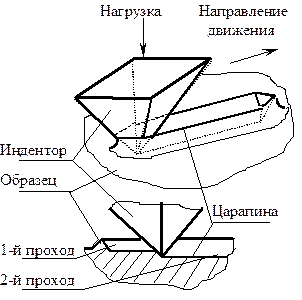
| 
| |
| Р и с. 3.18. Царапание поверхностного слоя индентором Виккерса | Рис. 3.19. Схема борозды | |
Выбор микротвердомера ПМТ-3 в качестве склерометра обоснован следующим:
прибор позволяет производить выбор места, глубины, направления и скорости царапания исследуемой поверхности без существенных ограничений;
благодаря углу при вершине индентора 136° царапины образуются в режиме пластической деформации, без микрорезания поверхностного слоя;
материал индентора (алмаз) долговечен и позволяет исключить образование наростов при царапании поверхности;
получаемые отпечатки имеют правильную призматическую форму, что позволяет без труда производить расчет вытесненного объема;
имеется возможность создания возвратно-поступательного движения столика за счет вращения ручного маховика, что позволяет производить циклическое деформирование материала поверхностного слоя с произвольным числом повторных проходов индентора.
При использовании метода склерометрии в качестве механического способа оттеснения поверхностного слоя энергия активации разрушения может оцениваться из отношения
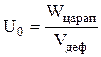 , (3.25)
, (3.25)
где Wцарап - механическая энергия, затраченная на царапание, кДж; Vдеф - количество активированного материала, моль.
Данное предположение может считаться справедливым при малых скоростях царапания <0.01 м/с, при которых можно пренебречь гидродинамическими свойствами пленок смазочных материалов, нанесенных на поверхность образца, саморазогревом поверхности образца в зоне контакта с индентором, а также влиянием скорости царапания на количество деформируемого вещества.
Выражение для расчета работы, затраченной на пропахивание канавки, имеет вид
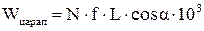 , (3.26)
, (3.26)
где N - нормальная нагрузка на индентор, H; f - коэффициент сопротивления царапания; L - путь трения (длина канавки), мкм; a - угол между векторами силы и скорости при царапании поверхностного слоя. Параметр a необходимо учитывать, поскольку материал поверхностного слоя является анизотропным. При этом деформация материала, преимущественно осуществляемая за счет механизма скольжения дислокаций, происходит в направлении, обусловленном ориентацией кристаллографических плоскостей металлических зерен. Оси главных напряжений в деформируемом материале поверхностного слоя вытягиваются вдоль направления сопротивления движению, поэтому можно принять 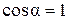 при царапании исследуемой поверхности вдоль образовавшейся текстуры (a = 0°), а также при ее поперечной деформации.
при царапании исследуемой поверхности вдоль образовавшейся текстуры (a = 0°), а также при ее поперечной деформации.
В процессе трения материал поверхностного слоя претерпевает многократную пластическую деформацию, что в конечном итоге приводит к исчерпанию запаса пластичности и охрупчиванию. Исследования метода склерометрии показали, что при многократных проходах индентора по одной борозде объем материала, вытесняемого при каждом проходе (за исключением первого), является одинаковым. При первом проходе вытесняемый индентором объем всегда оказывается больше, чем при втором и последующих проходах, что объясняется отличием деформации при первичном и последующем образовании борозды. Первичную борозду формируют «холмики», вырастающие по краям канавки. Последующее увеличение борозды при новых проходах происходит путем повторной деформации этих холмов и оттеснением наружу (см. рис. 3.19), подобно разрушению поверхностного слоя при трении, обусловленному малоцикловой усталостью при многократной пластической деформации «холмов». По этой причине объем борозды, полученной после первого прохода индентора, в анализе не учитывается.
При осуществлении многократных проходов индентора по исследуемой поверхности, среднее значение объема, вытесняемого за один проход, определяется как отношение полученного объема борозды к числу сделанных проходов. Объем борозды определяют исходя из ее геометрических характеристик: ширины D и длины L. Принимая, что глубина внедрения индентора hвн связана с шириной царапины соотношением hвн @0,14·D, и используя для расчета площади поперечного сечения борозды формулу площади треугольника 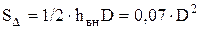 выражение для расчета количества вытесненного материала с учетом размерности примет вид:
выражение для расчета количества вытесненного материала с учетом размерности примет вид:
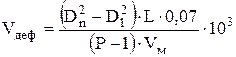 , (3.27)
, (3.27)
где Vм -молярный объем металла, мм3/моль; P - число проходов индентора; D1 и Dn - ширина борозды соответственно после 1 и P проходов индентора, мкм.
С учетом выражений (3.26-3.27) формула для расчета энергии активации примет следующий вид:
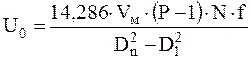 . (3.28)
. (3.28)
Чтобы получить корректную оценку энергии активации при использовании полученного выражения необходимо обосновать выбор параметров P и N, а также оценить значения f, Vм, D1 и Dn.
Ширину канавки можно оценить различными экспериментальными методами: измерением при помощи оптических приборов, путем снятия профилограммы щуповым прибором, сканированием поверхности на электронном микроскопе и др. Достаточную точность измерения ширины борозд позволяет получить оптический метод, реализованный на базе оптического микрометра ОМО (ГОСТ 7513-55), которыми снабжены микротвердомеры типа ПМТ-3. В этом случае образец необходимо установить таким образом, чтобы одна из неподвижных рисок на шкале микрометра легла вдоль одного края борозды, а подвижная риска - вдоль противоположного края. Увеличение микроскопа должно быть выбрано согласно требуемой точности измерения. Как показали эксперименты, для царапин глубиной в единицы и шириной в десятки микрон достаточную точность замеров можно получить при погрешности ±0,4 мкм/дел, что соответствует увеличению окуляра15x. Данный способ отличают малая трудоемкость, достаточная точность получаемых результатов, а также возможность игнорирования участков борозды со случайными дефектами поверхности, что особенно важно при исследовании приработанной поверхности. Недостатком метода является элемент субъективности при измерениях, когда точность результата связана с квалификацией экспериментатора.
При скольжении индентора по поверхности образца реализуется пластическое оттеснение материала. В случае, когда нормальные нагрузки на фактических площадях контакта близки к твердости материала, Боуден и Тейбор предложили использовать следующую зависимость, связывающую касательные и нормальные напряжения:
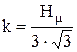 , (3.29)
, (3.29)
где k - касательное напряжение деформирования материала; Нm - микротвердость. Из уравнения следует, что коэффициент сопротивления царапанью пластического трения близок к величине 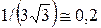 . Таким образом, при расчете энергии, затраченной на пластическую деформацию поверхностного слоя наиболее часто применяемых конструкционных материалов, коэффициент f можно считать постоянным, равным 0,2.
. Таким образом, при расчете энергии, затраченной на пластическую деформацию поверхностного слоя наиболее часто применяемых конструкционных материалов, коэффициент f можно считать постоянным, равным 0,2.
Молярный объем для чистых металлов рассчитывается по величине их атомной массы M и плотности r по формуле
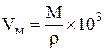 . (3.30)
. (3.30)
Для сплавов молярный объем определяется исходя из процентного содержания примесей по формуле
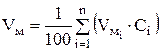 , (3.31)
, (3.31)
где n - количество элементов в сплаве; Vмi - молярный объем i-того элемента, рассчитываемый по (3.30); Сi - концентрация i-того элемента, % мас.
В процессе трения происходит текстурирование поверхностного слоя, что, однако, не вызывает качественного изменения свойств и кристаллического строения материала. Тепловое расширение - дилатация при пластической деформации не превышает сотых долей процента. Поскольку модифицированный со стороны свободной поверхности тонкий слой имеет размеры порядка 0,2¸3,0 нм, что значительно меньше толщины исследуемого слоя 0,1¸3,0 мкм, можно также считать, что модифицированное состояние не оказывает существенного влияния на оценки величины Vм. Поэтому расчетная формула (3.31) применима в случае модифицированной поверхности.
Табличные значения величины атомной массы М и плотности r для ряда металлов и сплавов, их элементный состав, а также рассчитанные значения Vм приведены в табл. 3.3.
| Таблица 3.3. | |||
| Молярный объем некоторых металлов и сплавов | |||
| Материал | Атомная масса М | Плотность r, 103 · кг/м3 | Молярный объем М, мм3/моль |
| Медь | 63,564 | 8,96 | |
| Алюминий | 26,982 | 2,6889 | |
| Железо | 55,847 | 7,874 | |
| Титан | 47,90 | 4,505 | |
| Никель | 58,70 | 8,91 | |
| Магний | 24,305 | 1,738 | |
| Хром | 51,996 | 7,18¸7,20 | ~7222 |
| Сталь легированная | - | 7,77¸7,85 | ~7160 |
| Латунь | - | 8,2¸8,85 | ~7999 |
| Бронза | - | 7,5¸9,1 | ~9464 |
Чтобы оценить деформационные характеристики материала в режиме малоцикловой усталости, число проходов должно быть больше двух. Первый проход индентора служит только для создания базовой борозды, относительно которой рассчитывается объем материала, вытесненного при последующих проходах (см. рис. 3.19). Поэтому объем исходной борозды в дальнейшем исключается из рассмотрения.
С увеличением числа проходов происходит рост борозды и возрастает площадь упругого контакта граней индентора с поверхностью царапины. Если число проходов превысит некоторое критическое значение Ркр, пластический характер контактирования сменится упругим, а пластическое трение сменится смешанным. При экспериментальных исследованиях было установлено, что данный переход имеет резко выраженный характер. Для гарантированного обеспечения точки бифуркации материала поверхностного слоя при механическом воздействии число проходов индентора не должно превышать Ркр. Критерий выбора оптимального числа проходов индентора имеет вид
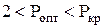 . (3.32)
. (3.32)
Величина Ркр для каждого материала требует экспериментальной оценки.
При выборе оптимального числа проходов желательно использовать значения, близкие к Ркр. Это дает возможность объективной оценки среднего количества активируемого материала. Многочисленные эксперименты показали, что для испытанных конструкционных металлов и сплавов диапазон оптимального числа проходов индентора находится в пределах 3¸5.
Нагрузка, действующая на индентор, влияет на глубину деформируемого слоя. Для объективной оценки энергии активации величину нагрузки следует выбирать исходя из твердости материала и толщины модифицированного слоя. Оптимальной является максимальная нагрузка, при которой глубина царапины не превышает толщины debris - слоя. Поэтому выбор N осуществляется на основании эксперимента.
В результате проведенных исследований была получена табл. 3.4, в которой указаны рекомендуемые значения N для различных материалов.
| Таблица 3.4. | ||
| Оптимальные нагрузки на индентор | ||
| Испытываемый материал | Рекомендуемая масса груза, Г | Характерная глубина исследуемого слоя, мкм |
| Покрытия | 15¸20 | 0,5 |
| Цветные металлы | 1¸3 | |
| Нецветные металлы, стали и сплавы | 1¸3 | |
Наиболее сложной активационной характеристикой для физического толкования является структурно-чувствительный коэффициент g. Ранее этот коэффициент
рассматривался как подгоночный параметр, связывающий величину энергии активации с действующим напряжением. В других работах физический смысл g интерпретировался согласно его размерности как активационный микрообъем, подверженный действию термической флуктуации. Кроме того, существуют работы, в которых при изучении кинетики деформации этот коэффициент не рассматривается вовсе. В настоящее время принято считать, что структурно-чувствительный коэффициент характеризует состояние материала поверхности, полученное в результате воздействия на нее физико-химических и механических факторов (термообработки, наклепа, смазки и т.д.).
В приведенной методике оценки энергии активации при механическом воздействии на материал поверхностного слоя контактные давления близки к твердости, поэтому при условии DG=0 коэффициент g можно определить непосредственно из выражения
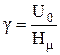 , (3.33)
, (3.33)
поскольку в условиях данной методики s @ Нm.
Дата добавления: 2015-07-06; просмотров: 1465;
