Дифференциальные уравнения движения СМТ

Глава 4. Дифференциальные уравнения

Движения СМТ и общие теоремы динамики СМТ

Дифференциальные уравнения движения СМТ

Пусть СМТ состоит из n МТ с постоянными массами m₁,m₂,…,m_n. Напомним, что через 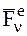обозначена равнодействующая внешних сил, а через 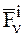– равнодействующая внутренних сил, действующих на n-ю МТ (рис. 29).

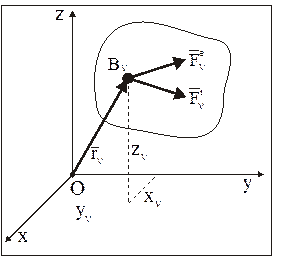
Рис. 29

Тогда на основании второго (основного) закона динамики в форме (1.2) для каждой МТ можно записать:

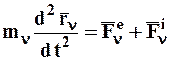(n=1, 2, ..., n). (4.1)

Система (4.1) является системой n дифференциальных уравнений движения СМТ в векторной форме.

Если спроектировать соотношения (4.1) на оси декартовой системы координат, то получим систему 3n дифференциальных уравнений движения СМТ в координатной форме:

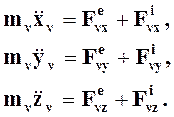n=1, 2, ..., n (4.2)

Следует отметить, что решение задач динамики с использованием системы уравнений (4.2) затруднено тем, что ее уравнения, кроме 3n функций

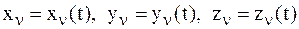
содержат еще и внутренние силы. Поэтому решение задач динамики с помощью системы уравнений (4.2) может потребовать дополнительных соотношений. Кроме того, значительное количество МТ может привести к громоздкости системы (4.2).