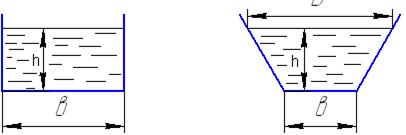
Геометрические элементы сечения каналов

Прямоугольное сечение Трапецеидальное сечение

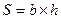
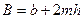(12.7)

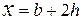
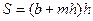(12.8)

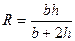
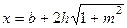(12.9)

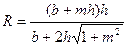(12.10)

12.4. Основные типы задач по расчёту открытых каналов

При расчёте каналов встречаются следующие три типовые задачи; решения их покажем для наиболее часто встречающихся трапецеидальных каналов симметричного профиля.

Задача 1. Заданы: ширина канала по дну b, глубина потока в канале h, величина откоса m, коэффициент шероховатости n и уклон дна канала .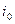

Определить: расход воды в канале Q.

Решение задачи сводится к определению по данным ранее формулам величин S, 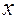, R, C и к подстановке этих величин в (12.2).

Задача 2. Заданы: расход воды в канале Q, ширина канала по дну b, глубина воды в канале h, величина откоса m и коэффициент шероховатости n.

Определить: уклон дна канала .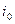

Вначале находятся величины S, 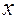, R и C, затем уклон определяется из формулы Шези (12.2)

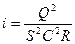. (12.11)

Задача 3. Заданы: расход воды в канале Q, ширина канала по дну b, величина откоса m, коэффициент шероховатости n и уклон дна канала .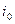

Определить: глубину потока в канале h.

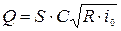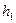В данном случае необходимо решить одно уравнение с одним неизвестным h. Аналитически эту задачу решить невозможно; ее решают обычно на ЭВМ или методом подбора. Метод подбора в данном случае состоит в сведении задачи 3 к решению ряда задач 1,задаваясь при этом различными значениями h и находя соответствующие значения Q. Задавшись любым значением (проще всего вначале принимать 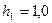м), определяют расход 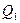и

Рис. 12.2 сравнивают его с заданным расходом Q. В зависимости от соотношения 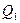и Q берут 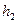больше или меньше 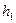и снова находят 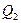.Определив величину Q 3-4 раза, необходимо построить кривую Q=f(h) (рис.12.2). По полученной кривой и заданному расходу определяют глубину h – глубину равномерного движения в канале при заданном расходе – нормальную глубину.

Учитывая важность понятия нормальной глубины, дадим её определение ещё раз.