Равномерное движение воды в открытых руслах
12.1. Условия равномерного движения
Все открытые русла делятся на естественные и искусственные. Естественные русла (реки, ручьи, временные водостоки) характеризуются тем, что очертание ложа в живом сечении не имеет какой-либо правильной геометрической формы. К искусственным руслам относятся каналы, безнапорные трубы-тоннели, канализационные и дренажные трубы. Характерной особенностью искусственных русел является то, что они в большинстве случаев имеют правильную форму поперечного сечения. Напомним, что безнапорное движение во всех открытых руслах характеризуется тем, что они имеют свободную поверхность с одинаковым (атмосферным) давлением.
 Равномерным движением в открытом русле называется такое установившееся движение, когда форма и площадь сечения потока, а, следовательно, и средняя скорость остаются постоянными по всей длине русла (рис.12.1). Глубина в любом сечении отсчитывается вдоль перпендикуляра к дну в данной точке, как показано на рис.12.1. Для того, чтобы движение было равномерным, необходимо, чтобы выполнялись следующие условия:
Равномерным движением в открытом русле называется такое установившееся движение, когда форма и площадь сечения потока, а, следовательно, и средняя скорость остаются постоянными по всей длине русла (рис.12.1). Глубина в любом сечении отсчитывается вдоль перпендикуляра к дну в данной точке, как показано на рис.12.1. Для того, чтобы движение было равномерным, необходимо, чтобы выполнялись следующие условия:
 1. Постоянство расхода воды (Q=const). (12.1)
1. Постоянство расхода воды (Q=const). (12.1)

 2. Постоянство живого сечения (S=const), а, следовательно, и средней скорости (V=const).
2. Постоянство живого сечения (S=const), а, следовательно, и средней скорости (V=const).
3. Постоянство уклона дна, равного уклону свобод-
Рис. 12.1 ной поверхности.
Кроме того, необходимо, чтобы шероховатость русла на рассматриваемом участке была однотипна и отсутствовали бы местные сопротивления. На практике все приведённые условия в точности почти никогда не выполняются. Однако, если отклонения от этих условий невелики, то движение в открытом русле считается равномерным. Наименьшие отклонения от условий равномерного движения воды в открытых руслах имеют место в искусственных руслах-каналах.
12.2. Основные расчётные формулы
Основной расчётной зависимостью для установившегося равномерного движения воды в открытых руслах является формула Шези:
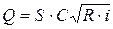 , (12.2)
, (12.2)
где Q – расход воды в канале; S – площадь сечения; R – гидравлический радиус; i – уклон дна канала; C – коэффициент Шези.
Обозначая
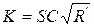 ,
,
получим формулу Шези в таком виде:
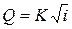 , (12.3)
, (12.3)
где K называется расходной характеристикой.
Коэффициент Шези C определяется по ряду эмпирических формул:
1. Формула Н.Н. Павловского
 , (12.4)
, (12.4)
где R – гидравлический радиус, м; n – коэффициент шероховатости
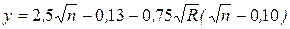 , (12.5)
, (12.5)
т.е. показатель y является функцией коэффициента шероховатости и гидравлического радиуса:
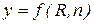 .
.
2. Формула И.И. Агроскина
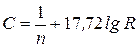 . (12.6)
. (12.6)
Дата добавления: 2015-08-01; просмотров: 1413;
