Сила, с которой жидкость действует на погруженное в нее тело, равна весу жидкости, вытесненной телом, и направлена вертикально вверх.
Сила Архимеда может быть найдена по формуле
F= 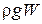 ,
,
где 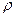 – плотность жидкости; W – объем тела; g – ускорение свободного падения;
– плотность жидкости; W – объем тела; g – ускорение свободного падения; 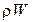 – масса жидкости в объеме тела;
– масса жидкости в объеме тела; 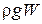 – вес жидкости в объеме тела.
– вес жидкости в объеме тела.
Сила Архимеда действует на тела, находящиеся в жидкостях и газах, т.е. практически на все тела в природе; она является поверхностной силой и при полном погружении тела в однородную жидкость не зависит от глубины погружения.
Задача 7.10.Сколько деревянных бревен каждое длиной l=3 м и диаметром
d=0,3 м нужно связать, чтобы сделать плот, удерживающий на плаву груз массой m=2000 кг, плотность дерева 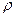 =500 кг/м3, плотность воды
=500 кг/м3, плотность воды 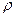 в=1000 кг/м3?
в=1000 кг/м3?
Решение.Предельной нагрузка будет считаться тогда, когда каждое бревно погрузится в воду и подъемная сила всего плота будет равна его весу вместе с грузом. Объем каждого бревна W как цилиндра равен W= 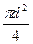 l=3∙3,14∙(0,3)2/4=0,21 м3. Вес одного бревна Р=
l=3∙3,14∙(0,3)2/4=0,21 м3. Вес одного бревна Р= 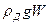 =500∙9,81∙0,21=1029 Н. Сила Архимеда, действующая на каждое бревно, равна Fa=
=500∙9,81∙0,21=1029 Н. Сила Архимеда, действующая на каждое бревно, равна Fa= 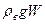 =1000∙9,8∙0,21=2058 Н. Одно бревно обладает способностью удержать 1029 Н. Весь груз массой 2000 кг весит Р´=mg=2000∙9,8=19600 Н. Если на изготовление плота необходимо n бревен, тогда
=1000∙9,8∙0,21=2058 Н. Одно бревно обладает способностью удержать 1029 Н. Весь груз массой 2000 кг весит Р´=mg=2000∙9,8=19600 Н. Если на изготовление плота необходимо n бревен, тогда
n∙1029∙H=19600 H
n= 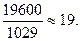
Таким образом, достаточно 19 бревен.
Задача 7.11.Полый медный шар диаметром d=5 см плавает в воде в состоянии безразличного равновесия. Найти толщину стенок шара. Плотность воды 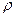 в=1000 кг/м3, плотность меди
в=1000 кг/м3, плотность меди 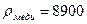 кг/м3.
кг/м3.
Решение.Из условия задачи следует, что выталкивающая сила, действующая на шар равна весу шара. Объем шара равен W=4/3 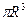 , а выталкивающая сила F=4/3
, а выталкивающая сила F=4/3 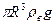 . Если принять, что радиус полости внутри шара равен r, то объем всей меди в стенке шара равен 4/3
. Если принять, что радиус полости внутри шара равен r, то объем всей меди в стенке шара равен 4/3 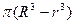 , а вес меди (а следовательно, и шара) равен 4/3
, а вес меди (а следовательно, и шара) равен 4/3 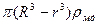 . Приравнивая выталкивающую силу и вес, получим равенство
. Приравнивая выталкивающую силу и вес, получим равенство
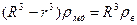 ,
,
из которого можно определить r, а следовательно, и толщину стенок.
Дата добавления: 2015-08-01; просмотров: 1270;
