Уравнение Бернулли для идеальной жидкости

Представим поток идеальной жидкости конечных размеров и выберем в нем произвольные сечения 1 и 2 (рис. 8.2). Вместе с жидкостью, протекающей за единицу времени через сечение 1, вносится энергия

E₁= 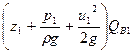, (8.6)

где 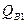– весовой расход жидкости в этом сечении, причем ;
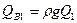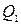– расход (объемный) через сечение 1. Энергия, уносимая жидкостью, вытекающей за единицу времени через сечение 2, равна

E₂= 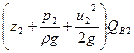. (8.7)

При установившемся течении расход в любом сечении потока постоянный, т.е. 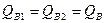. В случае идеальной жидкости, когда трение полностью отсутствует, полная энергия жидкости между сечениями 1 и 2 сохраняет свою величину постоянной независимо от времени, поэтому выполняется условие

E₁=E₂

и, следовательно

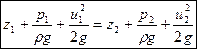. (8.8)

Последнее равенство следует из закона сохранения энергии: полная механическая энергия потока идеальной жидкости в любом сечении принимает одинаковые значения. Линия полной энергии на рис. 8.2 представляет горизонтальную линию. Ниже приводятся примеры применения уравнения Бернулли.

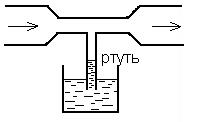
Задача 8.1. Поток переходит из узкого сечения трубы в широкое. Определить, в каком сечении - узком или широком - давление больше. Жидкость считать идеальной.

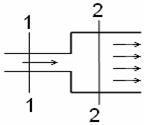Решение. Представим трубу горизонтальной (рис. 8.3), выберем два сечения 1-1 и 2-2 и плоскость отсчета, совпадающую с осью трубы. Уравнение Бернулли для данного случая ( 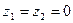) преобразуется так

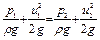
или

.

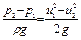Очевидно, что 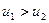(как следует из уравнения нераз- Рис. 8.3

рывности) и правая часть больше нуля. Следовательно, и левая часть последнего равенства положительна, поэтому 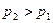- давление в широкой части трубы больше.

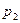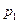Этот результат можно получить и другим путем. Считая жидкость идеальной, мы уверены, что происходит лишь превращение одного вида механической энергии в другой (без перехода в тепло). Кинетическая энергия жидкости при переходе от сечения 1-1 к сечению 2-2 уменьшается. Следовательно, потенциальная энергия возрастает и > .Если представить поток в трубе, как показано на рис. 8.4, то в узком сечении дав- Рис. 8.4

ление будет меньше, чем в широком. Если к тому же жидкость вытекает в атмосферу, то давление в узком сечении меньше атмосферного и жидкость в трубке поднимается. Поднятие жидкости из бачка – признак того, что в узком сечении потока вакуум; таким образом, устройство на рис. 8.4 является простейшим насосом. В технике явление образования вакуума в узком сечении используется в водоструйных и пароструйных насосах (инжекторах). Необходимо заметить, что в узком сечении давление может быть во много раз больше атмосферного и рассмотренный нами процесс основан именно на том, что в широком сечении, расположенном вблизи узкого, давление равно атмосферному.

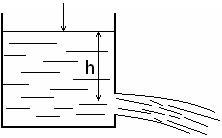
Задача 8.2. Определить скорость истечения жидкости из отверстия в открытом сосуде, рис. 8.5.

Решение. Если сосуд широкий, отверстие малое, то скорости внутри сосуда вдали от отверстия малы. Поэтому можно применить уравнение Бернулли (8.8) по всему потоку в целом и рассматривать его как один «поток». В верхнем сечении сосуда («потока») – у поверхности жидкости - давление 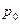равно атмосферному, а скорость 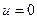. В нижнем сечении «потока» в отверстии – давление также равно атмосферному.

Если скорость в отверстии обозначить через 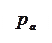V , то из (8.8) для этих двух сечений получим

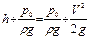
или

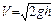, (8.9)

где h – высота уровня жидкости в сосуде.

Истечение происходит с той же скоростью,

Рис. 8.5 какую имело бы всякое тело при свободном падении с высоты h (без учета сопротивления воздуха).