Истечение при переменном напоре
Рассмотрим истечение из резервуара через отверстие без поступление в него жидкости извне. Этот процесс будет нестационарным – глубина жидкости в резервуаре (напор) будет изменяться.
Поставим задачу - определить время, в течении которого уровень жидкости резервуаре изменится на заданную величину.
Если скорость изменения уровня мала, то возможность применить уравнение Бернулли для установившегося движения и использовать зависимость для расхода Q при истечении, полученную выше.
Обозначим переменную высоту уровня жидкости в сосуде, отсчитываемую от дна, через h, площадь сечения резервуара на этом уравне S(h), а площадь отверстия So, рис.2.1.
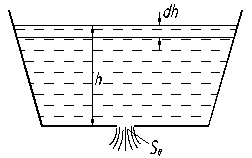 Рис 2.1.
Рис 2.1.
| За бесконечно малый интервал времени dt уровень в резервуаре понизится на величину dh и вытекший объём dw будет равен dw=S.dh. С другой стороны, через отверстие за время dt вытечет тот же самый объём dw, равный dw=Q.dt, где
|
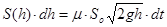
знак минус в (2.1) обусловлен тем, что положительному приращению dt соответствует отрицательное приращение dh (с увеличением времени уровень в резервуаре понижается).
Из (2.1) можно определить время изменения уровня от Н1 до Н2
|
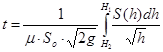 .
.
Хотя коэффициент расхода μ может зависеть от скорости истечения (а следовательно от h), его приближённо принимают постоянным.
Входящий в (2.2) интеграл может быть в случае резервуара произвольного сечения подсчитан одним из способов приближённого интегрирования.
Если S=const, то интеграл в (2.2) может быть подсчитан аналитически
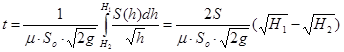 .
.
Время полного опорожнения резервуара (Н2=0) равно 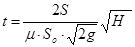 .
.
Задача 2.1 Круглый призматический резервуар высотой Н заполнен доверху водой. При открытии в его дне отверстия диаметром d он опорожняется полностью за время t0. Как изменится время t0 при одновременном
a) Уменьшение высоты Н в 4 раза;
b) Уменьшение диаметра отверстия d в 2 раза.
Дата добавления: 2015-08-01; просмотров: 1342;

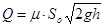 .
.