Истечение жидкостей из отверстия в тонкой стенке
При истечении жидкости из какого-либо резервуара происходит процесс превращения запаса потенциальной энергии в кинетическую энергию свободной струи. Основной вопрос исследования – определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.
Рассмотрим истечение жидкости через круглое отверстие в тонкой стенке (рис. 4.20). Отверстием в тонкой стенке называется отверстие, толщина стенок которого составляет не более 1/4 диаметра. Рассмотрим случай, когда жидкость вытекает из резервуара в атмосферу (см. рис. 4.20). Напишем уравнение энергии в форме напоров для сечения 1-1 и С-С. Обозначим давление на поверхности жидкости в резервуаре p0, 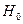 – заглубление центра отверстия под уровнем жидкости в сосуде. Струя, вытекающая под давлением столба жидкости высотой
– заглубление центра отверстия под уровнем жидкости в сосуде. Струя, вытекающая под давлением столба жидкости высотой 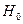 и разностью давлений
и разностью давлений 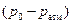 , при выходе из отверстия сжимается до сечения С-С. В сечении С-С струйки приблизительно параллельны и движение можно считать плавноизменяющимся, поэтому для этого сечения можно применить уравнение Бернулли. Такое сжатие обуславливается инерцией частиц жидкости, движущихся при подходе к отверстию по криволинейным траекториям. Степень сжатия струи оценивается коэффициентом
, при выходе из отверстия сжимается до сечения С-С. В сечении С-С струйки приблизительно параллельны и движение можно считать плавноизменяющимся, поэтому для этого сечения можно применить уравнение Бернулли. Такое сжатие обуславливается инерцией частиц жидкости, движущихся при подходе к отверстию по криволинейным траекториям. Степень сжатия струи оценивается коэффициентом
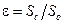 , ,
| (4.21) |
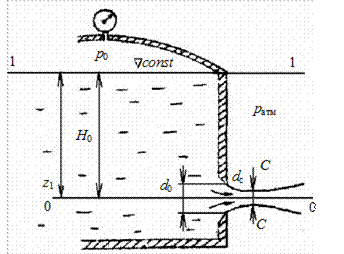
Рис. 4.20. Истечение жидкости из отверстия в тонкой стенке
где 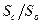 – отношение площади струи в сжатом сечении к площади отверстия.
– отношение площади струи в сжатом сечении к площади отверстия.
Для плоскости сравнения, проведенной относительно оси отверстия, запишем уравнение Бернулли для движения жидкости от свободной поверхности, где скорость можно принять равной нулю, до сечения С-С
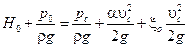 ,
,
где 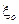 – коэффициент сопротивления отверстия.
– коэффициент сопротивления отверстия.
Выполним небольшие преобразования
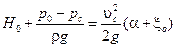 или
или 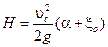 ,
,
где H – расчетный напор
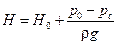 . .
| (4.22) |
Скорость истечения
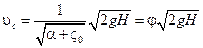 , ,
| (4.23) |
где φ– коэффициент скорости.
Нами получена формула Торричелли для определения скорости струи, вытекающей из резервуара.
Если резервуар открыт, то 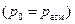 , тогда
, тогда
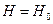 и и 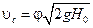 . .
| (4.24) |
Расход через сжатое сечение
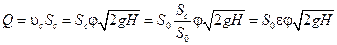 ,
,
где ε – коэффициент сжатия струи; 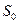 – площадь сечения отверстия.
– площадь сечения отверстия.
Окончательно получаем:
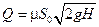 , ,
| (4.25) |
где μ – коэффициент расхода.
4.10. Зависимость коэффициентов истечения
от числа Рейнольдса
При истечении вязких жидкостей (например, дизельного топлива через форсунки) или при истечении с небольшими скоростями маловязких жидкостей (при малых числах Рейнольдса) будет проявляться зависимость величин коэффициентов истечения μ, φ, εот Re (см. рис. 4.21).
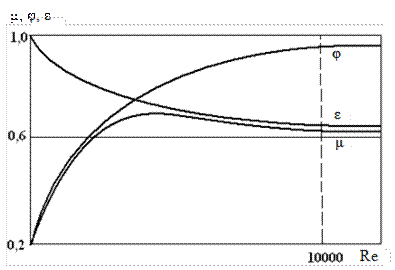
Рис. 4.21. Зависимость коэффициентов истечения от числа Рейнольдса
При истечении через малое отверстие в тонкой стенке коэффициент скорости φ с увеличением Re возрастает, что связано с уменьшение сил вязкости, что в свою очередь сказывается на уменьшении коэффициента сопротивления ξ. Коэффициент сжатия уменьшается вследствие увеличения радиусов кривизны поверхности струи на её участке от кромки до сжатого сечения С-С (см. рис. 4.22). При Re → ∞ значения коэффициентов φ и εприближаются к значениям, соответствующим истечению идеальной жидкости (φ = 1, ε = 0,6).
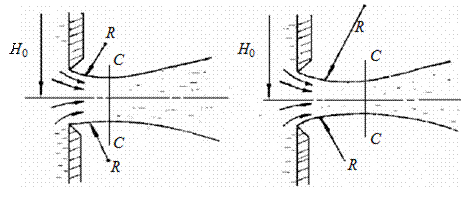
Рис. 4.22. Истечение жидкости из отверстия
Изменение величины коэффициента расхода μ определяется его зависимостью от коэффициентов φ и ε:
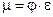 . .
| (4.26) |
Зная характер изменения коэффициентов μ, φ, ε от числа Re при истечении через отверстия и насадки, можно с большей точностью определить скорость 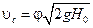 , расход Q и другие параметры потока.
, расход Q и другие параметры потока.
При больших числах Re (турбулентный режим) коэффициенты истечения постоянны, зависят только от вида отверстия, определяются опытным путем и приводятся в справочниках.
Дата добавления: 2015-08-26; просмотров: 2989;
