Методика эксперимента. С помощью газонаполненных ламп можно осуществить колебательные системы, содержащие только один накопитель энергии в отличие

С помощью газонаполненных ламп можно осуществить колебательные системы, содержащие только один накопитель энергии в отличие, например, от колебательного контура, содержащего два накопителя энергии - конденсатор и индуктивность. Такой системой являются цепи, содержащие конденсатор и сопротивление. Разряд конденсатора через сопротивление представляет собой апериодический процесс. Ему можно придать периодический характер, возобновляя заряд конденсатора через постоянные промежутки времени. Колебания в этом случае являются совокупностью двух апериодических процессов - процесса зарядки конденсатора и процесса его разрядки. Процесс зарядки конденсатора происходит в течение сравнительно длительного времени, затем очень резко, почти скачком, происходит его разряд. Такие колебания называются релаксационными (рис. 4.4). .

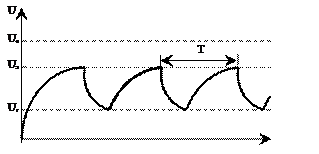
Рис. 4.

Рассмотрим работу генератора релаксационных колебаний. Принципиальная его схема приведена на рис. 4.3. Он состоит из источника постоянного напряжения U0 , конденсатора ёмкостью C, сопротивления R и лампы Л. Если включить источник тока, то в цепи появится ток. Сопротивление незажжённой лампы бесконечно велико, и ток будет заряжать конденсатор. Разность потенциалов на его обкладках будет расти. Соответственно растёт и разность потенциалов на электродах лампы, подсоединённой параллельно конденсатору. Когда она достигнет значения напряжения зажигания U3 , лампа «зажжётся» – её сопротивление скачком уменьшится, и она начнёт проводить ток. Так как сопротивление R велико, то поддерживать ток будут в основном заряды, расположенные на обкладках конденсатора. Это вызовет быстрое падение напряжения на конденсаторе, и когда оно достигнет значения напряжения гашения Uг, лампа «гаснет» и процесс начинается сначала. Кривая изменения напряжения на конденсаторе представлена на рис. 4.4.

Найдём закон, по которому будет меняться напряжение на конденсаторе. В любой момент времени величина напряжения U0 равна сумме напряжений в элементах цепи:

, (4.4)

где U - разность потенциалов на обкладках конденсатора. Заряд конденсатора изменяется вследствие протекания по цепи электрического тока:

(4.5)

Изменение заряда вызывает изменение разности потенциалов на обкладках конденсатора:

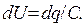(4.6)

Из уравнений (4.5) и (4.6) находим:

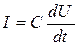. (4.7)

Подставляя соотношение (4.7) в уравнение (4.4), получаем:

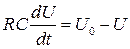. (4.8)

Уравнение (4.8) допускает разделение переменных и может быть записано в виде:

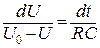. (4.9)

Интегрируя это уравнение, получим:

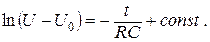(4.10)

Постоянная интегрирования находится из начального условия, что при t=0 U=0. Следовательно, const=lnU₀.

Потенцируя выражение (4.10), найдём закон возрастания напряжения на конденсаторе генератора релаксационных колебаний:

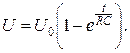(4.11)

Вычислим период колебаний генератора Т. Пусть t_з - момент времени, когда напряжение на лампе достигло значения напряжения зажигания, t_г- момент времени, когда лампа погасла, тогда Т=t_з-t_г. Определяя t_з и t_г из соотношения (4.11), получим:

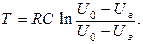(4.12)

Полученная формула является приближенной. У реальных генераторов период всегда несколько больше вычисленного (расхождение может доходить до 15 – 20%.). Такое расхождение объясняется тем, что при вычислении периода не были учтены предразрядные токи газоразрядной лампы. Действительно, когда напряжение на конденсаторе становится близким к напряжению зажигания, часть тока, проходящего через сопротивление R, ответвляется через лампу (предразрядный ток) и зарядка конденсатора замедляется. Кроме того, при релаксационных колебаниях разрядка конденсатора происходит до напряжения, более низкого, чем напряжение гашения лампы, определённое в статическом режиме. Этот факт легко объяснить тем, что в лампе, после того как перестанут существовать условия для образования разрядов, ток всё ещё продолжает течь до тех пор, пока не произойдёт полная деионизация газа.