Методика эксперимента. Рассмотрим случай слабой связи между контурами, т.е

Рассмотрим случай слабой связи между контурами, т.е. предположим, что С₁₂>>С. Тогда частоты нормальных колебаний ω₁ и ω₂ близки друг к другу и можно положить, что ω₁ ≈ ω₂ , (ω₁ + ω₂)=2 ω₁ ,а (ω₁ - ω₂)=Δω, где Δω << ω₁ . Тогда соотношения (5.8) и (5.9) можно переписать в виде:

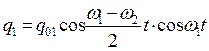, (5.10)

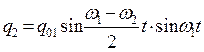, (5.11)

Получившиеся выражения (5.10) и (5.11) есть произведения двух колебаний. Вторые множители в них представляют собой быстро меняющиеся гармонические функции с частотой, близкой к частоте ω₁ ≈ ω₂, первые же множители обладают, в силу условия близости частот ω₁ и ω₂, малой частотой, т.е. большим периодом. 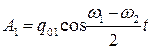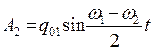Это позволяет рассматривать колебания зарядов q₁ и q₂ как почти гармонические с частотами ω₁ и медленно меняющимися амплитудами и соответственно. Подобные колебания изображены на рис. 5.3 и 5.4. Пунктирные линии представляют графики медленно меняющихся амплитуд. Сплошной линией на тех же рисунках представлены графики результирующих колебаний (5.10) и (5.11). Такое постепенное возрастание и убывание амплитуды носит название биений. Следует обратить внимание на то, что при t=0 амплитуда колебаний заряда на втором конденсаторе А₂ равна нулю. Амплитуда А₂ увеличивается, а амплитуда А₁ падает до тех пор, пока в момент времени, определённый из соотношения 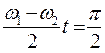, амплитуда А₁ не станет равной нулю, а амплитуда А₂ достигнет максимума.

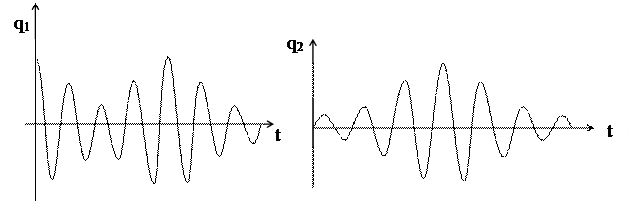Рис. 5.3. Зависимость 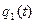Рис.5.4. Зависимость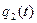

Ситуацию, показанную на рис. 5.3 и 5.4, можно рассмотреть с энергетической точки зрения.

При t=0 вся энергия сосредоточена в контуре 1. В результате связи через ёмкость С₁₂ энергия постоянно передаётся от контура 1 к контуру 2 до тех пор, пока вся энергия не соберется в контуре 2. Время, необходимое для перехода энергии из контура 1 в контур 2 и обратно, можно получить из уравнения :

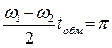, (5.12)

а частота, с которой контуры обмениваются энергией:

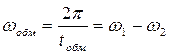. (5.13)

Для моды нормальных колебаний с частотой ω₁ токи текут в одинаковом направлении, тогда на емкости С₁₂ нет заряда. При этом частота ω₁ остаётся такой же, как для несвязанных контуров ω₁= 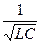=ω₀. В случае моды нормальных колебаний с частотой ω₂ емкость заряжена, что увеличивает частоту колебаний .

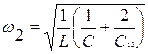В случае слабой связи выражение (5.13) можно преобразовать следующим образом:

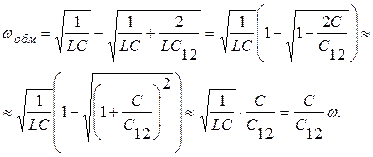(5.14)

Полученное значение частоты обмена энергией или частоты биений можно изменять, настраивая систему контуров, меняя параметры контуров С, С₁₂ и L. Период биений равен :

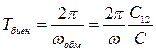. (5.15)

Исследование биений, т.е. обмена энергией в связанных контурах, и является одной из практических задач данной работы.

Мы рассмотрели работу схемы (рис. 5.2), предполагая, что омическое сопротивление в контурах отсутствует. В любом реальном контуре его сопротивление R отлично от нуля. Поэтому возникающие в связанных контурах колебания будут со временем затухать, т.е. амплитуды А₁ и А₂ со временем будут уменьшаться. На рис. 5.5 представлен график, определяющий реально существующие в контурах биения.

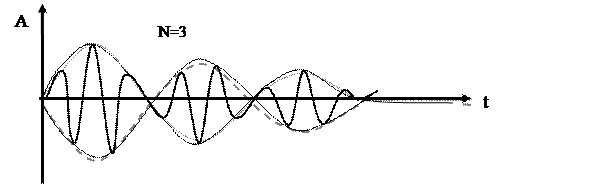
Рис. 5.5.Биения в реальных связанных контурах