Расчёт погрешностей

1. Определить среднее значения напряжений зажигания и гашения газоразрядной лампы по формуле П.1.

2. Вычислить среднеквадратическое отклонение величин этих напряжений от среднего значения по формуле П.2 .

3. Задать доверительную вероятность и определить по таблице П.1 коэффициент Стъюдента с учётом с числа измерений.

4. По формуле П.3 рассчитать величины абсолютных погрешностей.

5. Абсолютная погрешность измерения периода релаксационных колебаний определяется абсолютной погрешностью измерений интервалов времени с помощью осциллографа, которая в среднем составляет 10% от величины измеряемого интервала времени. Следовательно, абсолютная погрешность определения периода релаксационных колебаний: .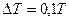

Лабораторная работа №5

ИЗУЧЕНИЕ ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ В СВЯЗАННЫХ КОНТУРАХ

Цель работы: изучение обмена энергии в системе электрических контуров, слабо связанных между собой, определение периода биений, сравнение результатов экспериментальных исследований с расчетными.

Основные понятия

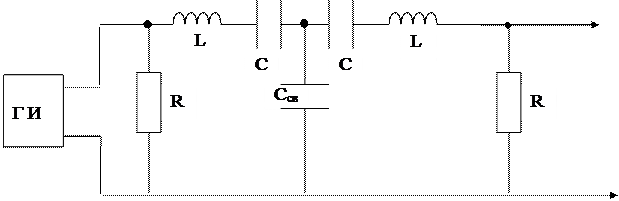
Связанными контурами называется электрическая цепь, состоящая из двух одинаковых колебательных контуров, связанных емкостью С_св (рис. 5.1). Колебания в контурах возбуждаются с помощью генератора импульсов ГИ.

Рассмотрим процессы, протекающие в связанных колебательных контурах, предполагая, что омические сопротивления R малы и ими можно пренебречь (рис. 5.2). На рис. 5.2 обозначены знаки зарядов на конденсаторах и положительные направления токов; С_св=С₁₂.

Рис. 5.2. Упрощённая схема связанных контуров

Запишем уравнения, описывающие колебания зарядов конденсаторов, соединённых по схеме (рис. 5.2):

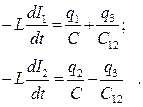(5.1)

По закону сохранения заряда, заряд на верхней обкладке конденсатора связи С₁₂ в каждый момент времени равен :

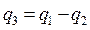. (5.2)

Подставляя в систему уравнений (1) соотношение (3) и учитывая, что 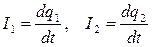, получим:

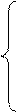
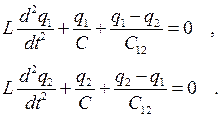(5.3)

Таким образом, процессы, происходящие в системе связанных контуров, описываются сложной системой связанных дифференциальных уравнений второго порядка. Для её решения введём новые переменные Q₁ и Q₂:

Q₁=q₁+q₂ и Q₂=q₁-q₂ . (5.4)

Тогда система уравнений (5.3) примет вид:

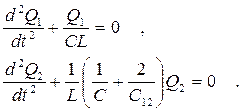(5.5)

Решения этих уравнений имеют вид

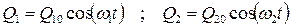, (5.6)

где

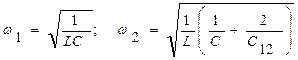. (5.7)

Таким образом, колебания, происходящие в связанных контурах, можно представить как совокупность двух несвязанных колебаний (5.6) с частотами ω₁ и ω₂. Введенные нами переменные Q₁ и Q₂ называются нормальными колебаниями или модами системы контуров, а частоты ω₁ и ω₂ называются нормальными частотами.

Пусть в начальный момент времени заряжается до заряда q₀₁ конденсатор в первом колебательном контуре, а конденсатор во втором контуре остаётся не заряжен, то есть q₀₂=0. Используя формулы (5.4) для нормальных колебаний и решения (5.6), получим закон изменения зарядов q₁ и q₂ на обкладках конденсаторов в связанных колебательных контурах от времени:

,

.

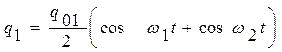Используя известные тригонометрические тождества, получим:

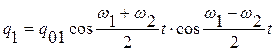, (5.8)

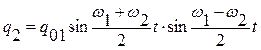. (5.9)