Методика эксперимента

Лабораторная работа № 1

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ( ) ЭЛЕКТРОНА

МЕТОДОМ МАГНЕТРОНА

Цель работы: изучить законы движения заряженных частиц в электрическом и магнитном полях; рассчитать величину удельного заряда электрона по критическому току в магнетроне.

Основные понятия

Большинство способов измерения заряда частиц основано на зависимости траектории движения частицы в электрическом и магнитном полях от величины удельного заряда частицы 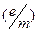( 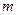- масса, а 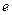- заряд частицы). Действительно, уравнение движения частицы в электрическом и магнитном полях имеет вид:

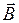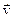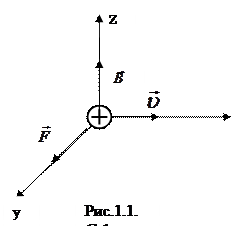
где - вектор напряжённости электрического поля, - вектор индукции магнитного поля. Первое слагаемое в правой части уравнения (1.1) представляет собой силу, действующую на заряд в электрическом поле, а второе - силу, действующую на движущийся со скоростью заряд в магнитном поле (силу Лоренца). Эта сила, как видно из соотношения (1.1), перпендикулярна той плоскости, в которой лежат вектора 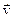и 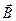(рис. 1.1).

Направление силы Лоренца

Практически направление силы Лоренца определяют так: сначала по правилу «правого винта» определяют направление вектора векторного произведения, а затем учитывают знак заряда движущейся частицы.

Как видно из уравнения (1.1), для измерения удельного заряда 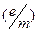недостаточно знать величины полей, потому что обычно неизвестна начальная скорость частицы.

В настоящей работе удельный заряд 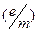электрона определяется с помощью метода, получившего название методa магнетрона. Это название связано с тем, что применяемая в работе конфигурация электрического и магнитного полей напоминает конфигурацию полей в магнетронах -генераторах электромагнитных колебаний в области сверхвысоких частот.

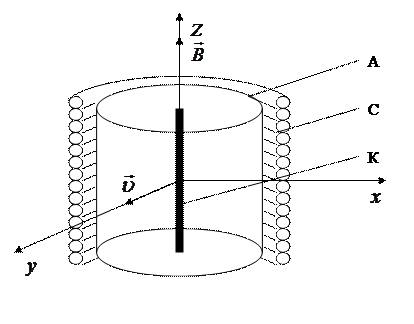
В нашем случае магнетрон представляет собой двухэлектродную электронную лампу (рис. 1.2). Анодом лампы служит цилиндр А, по оси которого натянута нить накала - катод К. Лампа помещается внутрь соленоида С.

При нагревании катода с его поверхности испускаются электроны (термоэлектронная эмиссия). Электрическое поле возникает между катодом и анодом, если к ним приложить разность потенциалов U, подавая на катод отрицательный, а на анод положительный потенциалы. Электрическое поле в такой системе направлено вдоль радиуса анода. При пропускании тока по соленоиду внутри него создается однородное магнитное поле, параллельное катоду. Тогда на электроны, вылетевшие из катода, действуют одновременно электрическое и магнитное поля.

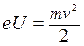, (1.2)

где v - скорость электрона у поверхности анода, U- разность потенциалов между катодом и анодом, e- заряд электрона, m- масса электрона.

В направлении, перпендикулярном к радиальному направлению, на электрон действует только сила Лоренца. Эта сила работы не совершает и лишь изменяет направление скорости. Величина скорости и кинетическая энергия заряда при его движении в магнитном поле не изменяются. Под действием силы Лоренца электрон равномерно движется по окружности радиуса 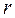, который может быть определён из уравнения движения электрона (1.1):

. (1.3)

Определяя отсюда радиус орбиты электрона r и, учитывая соотношение (1.2), получим :

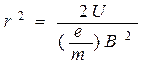. (1.4)

Из равенства (1.4) видно, что при заданном напряжении U увеличение индукции магнитного поля ведет к уменьшению радиуса траектории электронов. Несколько траекторий, соответствующих различным значениям индукции 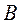, схематично представлены на рис. 1.3.

В отсутствии магнитного поля траектория движения электрона прямолинейна и направлена вдоль радиуса магнетрона (рис. 1.3,а).

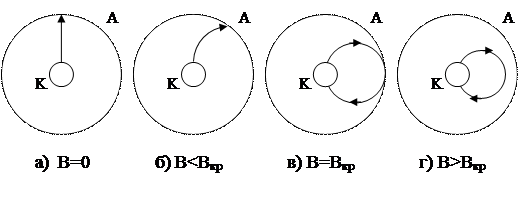
Рис. 1.3.Траетории движения электронов и «сбросовая» характеристика магнетрона

При слабом поле 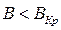(рис. 1.3,б) траектория электрона несколько искривляется, но электрон все же попадает на анод. При некотором критическом значении индукции магнитного поля 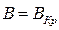(рис. 1.3,в) радиус траектории электрона становится равным (r_а-r_к)/2, так что он только касается анода (здесь r_а -радиус анода, а r_к­- радиус катода ). Наконец, при 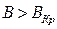(рис. 1.3,г) электрон вовсе не попадает на анод и возвращается к катоду; анодный ток становится равным нулю.

На рис. 1.3 показана «сбросовая» характеристика лампы: вследствие того, что испускаемые катодом электроны имеют разные начальные скорости, критические условия достигаются для разных электронов при разных значениях В, поэтому «сбросовая» характеристика имеет вид непрерывной кривой.

Методика эксперимента

Для нахождения величины удельного заряда электрона необходимо определить критическое значение индукции магнитного поля соленоида 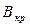. При значении магнитного поля, равном 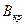, анодный ток резко падает. Если радиус анода много больше радиуса катода 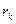, то траекторию электрона в цилиндрическом магнетроне можно считать окружностью с радиусом .

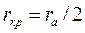Полагая в формуле (1.4) 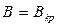и 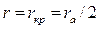, получим:

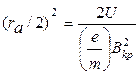. (1.5)

Отсюда удельный заряд электрона равен:

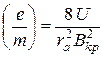. (1.6)

Индукция магнитного поля соленоида, у которого длина 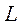соизмерима с диаметром , определяется формулой:

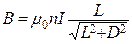, (1.7)
где 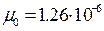Гн/м - магнитная постоянная; 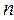- число витков соленоида на метр длины; - ток, протекающий по виткам соленоида.

Критическая величина магнитного поля 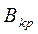будет наблюдаться при определённом значении тока в соленоиде:

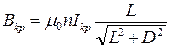. (1.8)

Подставляя значение В_кр из (1.8) в формулу для определения удельного заряда электрона (1.6), получаем: . . (1.9)

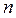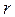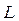Величины и , и 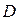являются для данной установки постоянными. Обозначим

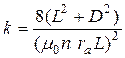. (1.10)

Тогда формула для определения удельного заряда электрона (1.9) перепишется в виде:

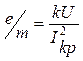. (1.11)

Из этой формулы следует, что найденные из опыта значения 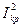должны быть пропорциональны 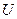. При определении 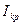из экспериментальной зависимости в качестве истинных лучше всего принимать значение тока при которых кривая имеет наибольший наклон. Естественно, что экспериментальные точки в этой области должны лежать особенно часто.