Лабораторная работа 3

ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ

В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Цель работы: изучение вынужденных колебаний в колебательном контуре; построение амплитудной резонансной кривой при разных значениях активного сопротивления контура; измерение резонансной частоты контура и исследование её зависимости от ёмкости конденсатора.

Основные понятия

Рассмотрим процессы, протекающие в колебательном контуре, подключенном к источнику, ЭДС которого изменяется по гармоническому закону (рис. 3.1).

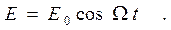(3.1)

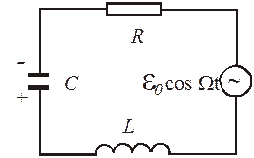
3.1.Колебательный контур

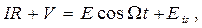(3.2)

где V– напряжение на конденсаторе с ёмкостью С; I– ток в контуре; R– его омическое сопротивление; Ω– частота вынуждающей ЭДС. Учитывая, что ЭДС самоиндукции 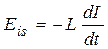, а ток в катушке равен

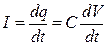, (3.3)
где q– заряд на обкладках конденсатора; L– индуктивность катушки.

Перепишем уравнение (3.1) в виде

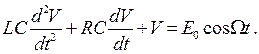(3.4)

Разделим это уравнение на LC и введем обозначения:

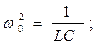
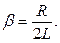
Тогда для определения зависимости напряжения на конденсаторе от времени получим следующее дифференциальное уравнение:

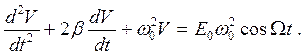(3.5)
Выражение (3.5) представляет собой уравнение вынужденных колебаний. Его решение складывается из общего решения однородного уравнения и частного решения неоднородного уравнения (3.5). Общее решение однородного уравнения известно и имеет вид:

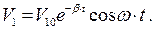(3.6)
Оно описывает затухающие колебания, которые через время 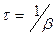практически прекращаются. Тогда решение уравнения (3.5) будет

определяться его частным решением, которое будем искать в виде:

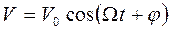, (3.7)
где V₀ и j подлежат определению; Ω - частота вынужденных колебаний, которая совпадает с частотой вынуждающей ЭДС. Подстановка решения (3.7) в уравнение (3.5) дает:

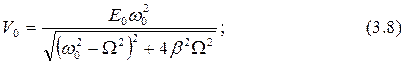
Таким образом, амплитуда и начальная фаза напряжения на конденсаторе зависят от соотношения частоты источника ЭДС W и частоты собственных колебаний контура w₀ .

Ток в контуре

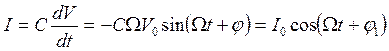, (3.10)

где .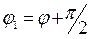

Амплитуда тока в контуре также зависит от соотношения частот W и w₀ и равна:

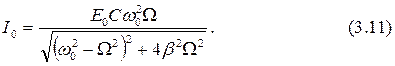
Кривые, описывающие зависимость амплитудных значений вынужденных колебаний напряжения и тока в контуре от частоты внешней силы, называются амплитудными резонансными кривыми. Максимального значения величина V₀ достигает при частоте внешней ЭДС, равной

. (3.12)
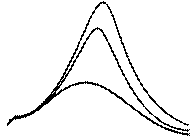
Резонансные кривые для V₀ изображены на рис. 3.2, а. При Ω=0 резонансные кривые стремятся к V_0стат напряжению, возникающему на конденсаторе при подключении его к источнику постоянного напряжения величины Е₀. Максимум при резонансе получается тем выше и острее, чем меньше β=R/2L, т.е. чем меньше активное сопротивление и больше индуктивность контура. При малом затухании (β²<<ω²₀ ) резонансная частота для напряжения близка к ω₀.

Колебания с максимальной амплитудой называются резонансными, а само явление «раскачки» колебаний до максимальной амплитуды называется резонансом. При отклонении частоты вынуждающей ЭДС от резонансной амплитуда резко уменьшается.

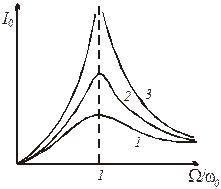
Резонансные кривые для силы тока представлены на рис. 3.2,б. Амплитуда силы тока (3.11) имеет максимальное значение 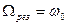, что совпадает с собственной частотой контура. Отрезок, отсекаемый резонансными кривыми на оси I₀, равен нулю, т.к. при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.

а б

Рис.3.2. Резонансные кривые: а − по напряжению, б − по току

Важной характеристикой колебательного контура является рост амплитуды V₀ в резонансе по сравнению с его статическим значением. Из (3.8) следует:

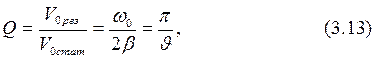
где θ − логарифмический декремент затухания. Величина Q называется добротностью контура. Соотношение (3.13) показывает, что чем меньше затухание в контуре, тем больше его добротность.

Если известны параметры контура, добротность может быть рассчитана по формуле:

Добротность контура характеризует также остроту резонансных кривых. Чтобы убедиться в этом, рассмотрим ширину резонансной кривой ΔΩ (рис. 3.4).

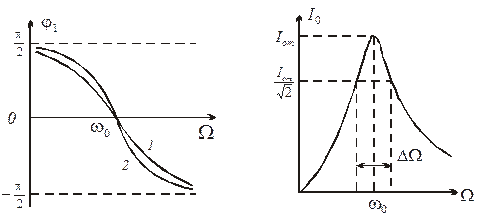
Рис. 3.3. Фазовые резонансные кривые Рис. 3.4. Построение полосы пропускания контура

Однако эта величина определяется не относительно амплитуды силы тока I₀, а относительно квадрата амплитуды. Это связано с тем, что такая важнейшая характеристика контура, как мощность, определяется не амплитудой I₀, а её квадратом. Шириной резонансной кривой называется расстояние в частотах ΔΩ от частоты резонанса ω₀ до той частоты, где квадрат амплитуды убывает в два раза ( I₀=I_0m/√2). Вычисления показывают, что ширина резонансной кривой равна:

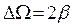, (3.15)

и чем меньше затухание, тем меньше ширина и острее резонансная кривая. Более удобно ширину резонансной кривой в (3.15) выразить через добротность:

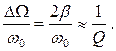(3.16)
Таким образом, ширина резонансной кривой ΔΩ=ω₀/Q, т.е. равна частоте резонанса, делённой на добротность.

Исследуем зависимость начальной фазы вынужденных колебаний от частоты вынуждающей ЭДС. График зависимости j₁ от частоты Ω представлен на рис. 3.3. Кривые I и 2 соответствуют разным значениям b; при и . Эти кривые называются фазовыми резонансными кривыми.