Расчёт погрешностей. Погрешность измеренной величины (e/m) в соответствии с соотношением (1.11) определяется для каждого значения анодного тока лампы
Погрешность измеренной величины (e/m) в соответствии с соотношением (1.11) определяется для каждого значения анодного тока лампы , как погрешность косвенного измерения [4] по следующей формуле:
 ,
,
где ΔU - абсолютная погрешность вольтметра; ΔIкр – абсолютная погрешность амперметра.
Лабораторная работа 2
ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА С ПОМОЩЬЮ ДАТЧИКА ХОЛЛА.
Цель работы: изучение эффекта Холла в металлах и применение для измерения индукции магнитного поля соленоида датчика Холла; измерение постоянной Холла и определение концентрации электронов в металле.
Основные понятия
Подобно тому, как в пространстве, окружающем электрические заряды, возникает электростатическое поле с определёнными физическими свойствами, так и в пространстве, окружающем токи, возникает особого вида поле, называемое магнитным. Силовой характеристикой магнитного поля является вектор магнитной индукции 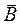 .
.
Закон, с помощью которого вычисляется магнитное поле постоянных токов, называется законом Био - Савара - Лапласа. Этот закон утверждает, что элемент длины dl проводника с током I создаёт в точке М магнитное поле, индукция которого dB пропорциональна длине dl, силе тока I, синусу угла α между направлением тока и радиусом - вектором 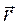 точки М и обратно пропорциональна квадрату расстояния r:
точки М и обратно пропорциональна квадрату расстояния r:
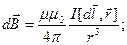
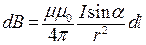 , (2.1)
, (2.1)
где μ0=4π·10-7 Ф/м - магнитная постоянная; μ- магнитная проницаемость среды, в которой создаётся магнитное поле.
Вектор магнитной индукции d 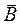 перпендикулярен к плоскости, содержащей элемент проводника с током
перпендикулярен к плоскости, содержащей элемент проводника с током 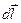 и радиус - вектор
и радиус - вектор 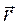 .
.
| |
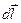 . Полный вектор магнитной индукции представляет собой векторную сумму всей полей d
. Полный вектор магнитной индукции представляет собой векторную сумму всей полей d 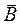 , создаваемых всеми элементами, на которые мы мысленно разбиваем проводник. Закон Био- Савара- Лапласа позволяет рассчитать магнитное поле проводников с токами простейшей формы, например, прямого бесконечно длинного проводника, в центре кругового тока и т.п.
, создаваемых всеми элементами, на которые мы мысленно разбиваем проводник. Закон Био- Савара- Лапласа позволяет рассчитать магнитное поле проводников с токами простейшей формы, например, прямого бесконечно длинного проводника, в центре кругового тока и т.п.
|
| |
| |
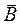 .
.
Циркуляцией вектора 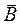 по заданному замкнутому контуру L называется интеграл следующего вида:
по заданному замкнутому контуру L называется интеграл следующего вида: 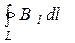 , где направление обхода по контуру также должно быть задано. Величина
, где направление обхода по контуру также должно быть задано. Величина 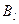 - проекция вектора
- проекция вектора 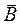 на направление касательной к контуру.
на направление касательной к контуру.
Можно доказать, что циркуляция вектора 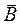 вдоль произвольного замкнутого контура L равна умноженной на μ0 алгебраической сумме токов, охватываемых этим контуром:
вдоль произвольного замкнутого контура L равна умноженной на μ0 алгебраической сумме токов, охватываемых этим контуром:
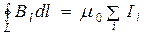 . (2.2)
. (2.2)
Теорему о циркуляции 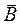 в электротехнике принято называть законом полного тока. Эта теорема в теории магнетизма играет такую же роль, как теорема Гаусса в электростатике. В частности, теорема о циркуляции
в электротехнике принято называть законом полного тока. Эта теорема в теории магнетизма играет такую же роль, как теорема Гаусса в электростатике. В частности, теорема о циркуляции 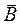 позволяет рассчитать индукцию магнитного поля бесконечно длинного соленоида без применения закона Био - Савара - Лапласа.
позволяет рассчитать индукцию магнитного поля бесконечно длинного соленоида без применения закона Био - Савара - Лапласа.
Соленоидомназывается совокупность одинаковых последовательно соединенных витков, равномерно навитых на общий каркас или сердечник.
Если длина соленоида во много раз больше диаметра его витков, то соленоид можно считать бесконечно длинным. Пусть по соленоиду течёт постоянный ток I. Магнитное поле такого соленоида целиком сосредоточено внутри него. Вне соленоида магнитное поле отсутствует. Внутри соленоида индукция магнитного поля параллельна его оси, и по величине равна
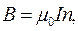 (2.3)
(2.3)
где n - число витков, приходящихся на единицу длины соленоида. Выражение (2.3) показывает, что во всех точках внутри бесконечно длинного прямого соленоида индукция магнитного поля одинакова по величине и направлению. Таким образом, магнитное поле соленоида однородно. Формула (2.3) справедлива для достаточно длинного соленоида вдали от его концов. При приближении к концам соленоида магнитная индукция падает.
Магнитные измерения охватывают широкий круг вопросов: изучение физических свойств ферромагнетиков, определение поля электромагнитов или электрических машин, изучение магнитного поля Земли, определение дефектов в материалах (магнитная дефектоскопия) и т.д. Несмотря на разнообразие задач, существует единая методика магнитных измерений, которая в каждом конкретном случае меняется незначительно. Обычно измеряется электрическая величина, являющаяся функцией магнитного поля.
Это измерение позволяет затем определять величину поля расчётным путём.
Дата добавления: 2015-08-01; просмотров: 1658;
