Некоторые сведения о символическом методе расчёта цепей синусоидального тока
Символический метод основан на представлении токов и напряжений, а также сопротивлений, проводимостей и мощностей в виде комплексных чисел.
В отличие от действительных чисел, которые являются точками на числовой оси, комплексное число представляет собой более общее понятие числа и изображается точкой на числовой плоскости с прямоугольной системой координат +1, + j.
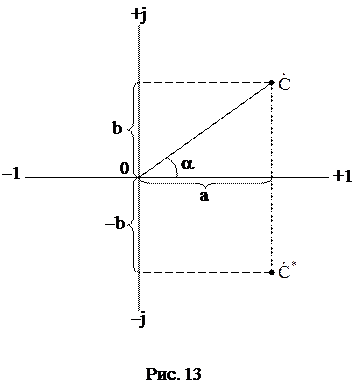
На рис. 13 комплексное число 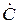 представлено в виде точки с координатами: a по оси вещественных +1 и b по оси мнимых +j величин. Комплексное число может быть представлено в виде
представлено в виде точки с координатами: a по оси вещественных +1 и b по оси мнимых +j величин. Комплексное число может быть представлено в виде 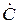 =а+jb (алгебраическая форма записи), где a - вещественная (Re) часть числа, b - мнимая (Im) часть комплексного числа, то есть a=Re
=а+jb (алгебраическая форма записи), где a - вещественная (Re) часть числа, b - мнимая (Im) часть комплексного числа, то есть a=Re 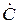 , b=Im
, b=Im 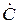 . Мнимая единица j=
. Мнимая единица j= 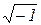 , (j2=-1), (-j2=+1).
, (j2=-1), (-j2=+1).
Отрезок c, измеряемый от начала координат до точки 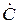 (см. рис. 13), называется модулем (mod) комплексного числа. Угол a, измеряемый между отрезком c и осью вещественных +1, называется аргументом (arg) комплексного числа, то есть c =mod
(см. рис. 13), называется модулем (mod) комплексного числа. Угол a, измеряемый между отрезком c и осью вещественных +1, называется аргументом (arg) комплексного числа, то есть c =mod 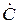 , a = arctg
, a = arctg 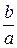 = arg
= arg 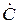 .
.
Кроме алгебраической, существует еще две равнозначные ей формы записи комплексного числа: тригонометрическая 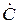 = c cosa + jc sina и показательная
= c cosa + jc sina и показательная 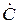 = с e ja. На практике обычно используются две формы записи: алгебраическая и показательная.
= с e ja. На практике обычно используются две формы записи: алгебраическая и показательная.
Сложение и вычитание комплексных чисел удобнее производить в алгебраической форме записи, а умножение и деление - в показательной.
Множитель e ja в показательной форме записи комплексного числа 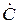 = c e ja
= c e ja
называется оператором поворота вектора на угол a в положительном направлении (против часовой стрелки). В частности, умножив положительную полуось действительных величин +1 на оператор 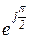 = cos
= cos 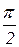 +j sin
+j sin 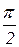 =+j, получим новый вектор +j, то есть положительную полуось мнимых величин. Таким образом: +j – оператор поворота на 900 против часовой стрелки, а -j - оператор поворота на 900 по часовой стрелки (в отрицательном направлении).
=+j, получим новый вектор +j, то есть положительную полуось мнимых величин. Таким образом: +j – оператор поворота на 900 против часовой стрелки, а -j - оператор поворота на 900 по часовой стрелки (в отрицательном направлении).
Сопряжённым комплексным числом 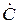 * (рис. 13) называется такое, которое отличается от исходного комплексного числа
* (рис. 13) называется такое, которое отличается от исходного комплексного числа 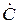 только знаком мнимой части (знаком аргумента в показательной форме записи).
только знаком мнимой части (знаком аргумента в показательной форме записи).
Если комплексное число имеет вид 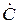 = a+jb= c e ja, то сопряжённое с ним число
= a+jb= c e ja, то сопряжённое с ним число 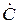 *= a-jb= c e -ja. Нетрудно убедиться, что произведение сопряжённых комплексных чисел есть вещественное число, равное квадрату модуля
*= a-jb= c e -ja. Нетрудно убедиться, что произведение сопряжённых комплексных чисел есть вещественное число, равное квадрату модуля 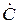
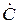 *= c2= a2+ b2.
*= c2= a2+ b2.
Поскольку синусоидальные токи и напряжения изображаются векторами, то, совместив начало каждого вектора с началом координат 0 комплексной плоскости, можно утверждать, что конец вектора (точка) является комплексным числом, а длина вектора (модуль комплексного числа) с учетом масштаба представляет собой величину соответствующего тока или напряжения.
Принято обозначать комплексы токов, напряжений и мощностей соответствующими буквами с точками наверху ( 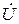 ,
, 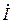 ,
, 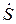 ). Комплексы сопротивлений и проводимостей, которые не являются гармоническими функциями времени, индексируют подчеркиванием внизу (
). Комплексы сопротивлений и проводимостей, которые не являются гармоническими функциями времени, индексируют подчеркиванием внизу (  ,
, 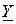 ).
).
Рассмотрим переход от параметрического метода расчёта к символическому на примере закона Ома для цепи с последовательным соединением активного r, индуктивного xL и ёмкостного xC сопротивлений. Закон Ома в параметрическом методе записывается в виде: I= 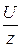 =
= 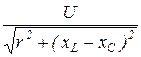 , где z=
, где z= 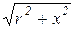 - полное сопротивление цепи (гипотенуза треугольника сопротивлений), r и x=xL - xC – активное и реактивное сопротивления цепи (катеты треугольника сопротивлений). Угол j в треугольнике сопротивлений j = arctg
- полное сопротивление цепи (гипотенуза треугольника сопротивлений), r и x=xL - xC – активное и реактивное сопротивления цепи (катеты треугольника сопротивлений). Угол j в треугольнике сопротивлений j = arctg 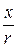 - угол сдвига по фазе между током I и напряжением U на входе цепи.
- угол сдвига по фазе между током I и напряжением U на входе цепи.
 |
Предположим, что цепь имеет индуктивный характер (xL > xC) и перенесём векторную диаграмму напряжения и тока в комплексную плоскость, совместив начала векторов с началом координат +1, +j. Очевидно концы векторов
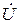 и
и 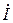 (точки) представляют собой комплексы действующих значений напряжения и тока (рис. 14).
(точки) представляют собой комплексы действующих значений напряжения и тока (рис. 14).
Умножив вектор тока 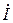 на вещественное число (скаляр) z, получим вектор
на вещественное число (скаляр) z, получим вектор 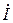 z, равный по длине вектору
z, равный по длине вектору 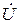 , но сонаправленный с вектором тока
, но сонаправленный с вектором тока 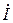 . Чтобы получить истинное положение вектора
. Чтобы получить истинное положение вектора 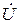 на диаграмме (рис. 14), необходимо умножить вектор
на диаграмме (рис. 14), необходимо умножить вектор 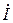 z на оператор поворота e jj на угол j в положительном направлении (против часовой стрелки). Таким образом можно записать:
z на оператор поворота e jj на угол j в положительном направлении (против часовой стрелки). Таким образом можно записать:
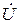 =(
=( 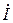 z) e jj=
z) e jj= 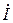 (z e jj)=
(z e jj)= 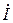
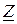 , где
, где 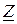 =z e jj=z cosj +jzsinj =r +j(xL - xC)= r +jxL --jxC = r+jx – комплексное сопротивление цепи, r=z cosj =Re
=z e jj=z cosj +jzsinj =r +j(xL - xC)= r +jxL --jxC = r+jx – комплексное сопротивление цепи, r=z cosj =Re 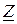 - активное, x=z sinj =Im
- активное, x=z sinj =Im 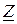 - реактивное сопротивление цепи.
- реактивное сопротивление цепи.
Очевидно выражение 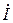 =
= 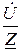 - представляет собой закон Ома для последовательной цепи в комплексной форме.
- представляет собой закон Ома для последовательной цепи в комплексной форме.
По аналогии можно записать в комплексной форме законы Кирхгофа:
I закон: 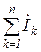 =0 – алгебраическая сумма комплексов токов в узле равна нулю;
=0 – алгебраическая сумма комплексов токов в узле равна нулю;
II закон: 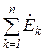 =
= 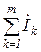
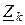 - алгебраическая сумма комплексов ЭДС в замкнутом контуре равна алгебраической сумме комплексов падений напряжения в ветвях, образующих этот контур.
- алгебраическая сумма комплексов ЭДС в замкнутом контуре равна алгебраической сумме комплексов падений напряжения в ветвях, образующих этот контур.
Комплексная проводимость эквивалентной разветвлённой цепи:
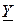 =
= 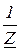 =
= 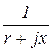 =
= 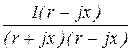 =
= 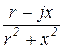 =
= 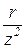 -j
-j 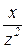 = g - jb = y e-jj, где g=
= g - jb = y e-jj, где g= 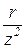 , b=
, b= 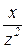 , y=
, y= 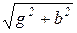 - активная, реактивная и полная проводимости.
- активная, реактивная и полная проводимости.
Обратный эквивалентный переход:
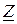 =
= 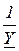 =
= 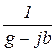 =
= 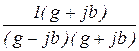 =
= 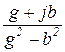 =
= 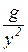 +j
+j  =r+jx= z ejj, где r=
=r+jx= z ejj, где r= 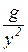 , x=
, x=  , z=
, z= 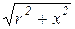 - активное, индуктивное и полное сопротивления. Следует обратить внимание, что при эквивалентных переходах от последовательной цепи к параллельной и наоборот знак реактивной составляющей изменяется на противоположный.
- активное, индуктивное и полное сопротивления. Следует обратить внимание, что при эквивалентных переходах от последовательной цепи к параллельной и наоборот знак реактивной составляющей изменяется на противоположный.
В символическом методе расчёта вводится понятие о комплексной мощности, которая представляет собой произведение комплекса напряжения на сопряжённый комплекс тока.
 |
На рис. 15 приведена векторная диаграмма для цепи, рассмотренной ранее (рис. 14), и отличающейся тем, что на ней показаны начальные фазы напряжения yU и тока yI (диаграммы строятся для момента времени t=0).Очевидно yU -yI=j.
Комплексы векторов напряжения и тока в показательной форме имеют вид: 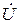 =U
=U 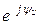 ;
; 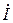 =I
=I 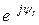 .
.
Сопряжённый комплекс тока 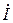 *=I
*=I 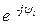 .
.
Комплексная мощность (по определению)
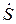 =
= 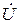
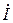 *=U I
*=U I 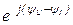 = U I e jj=U I cosj +jU I sinj =P+jQ, где P=Re
= U I e jj=U I cosj +jU I sinj =P+jQ, где P=Re 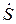 - активная мощность ,Q=Im
- активная мощность ,Q=Im 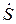 - реактивная мощность.
- реактивная мощность.
Приложение 3
Перечень основных вопросов, предлагаемых при защите курсовой работы "Электрические цепи трёхфазного тока"
1. Трёхфазные цепи. Основные определения и термины. Простейший генератор трёхфазного тока. Соединение звездой и треугольником, соотношения между фазными и линейными напряжениями и токами.
2. Схема трёхфазной цепи соединённой звездой. Симметричная и несимметричная нагрузка. Напряжение смещения нейтрали. Роль нейтрального провода. Векторные диаграммы.
3. Схема соединения трёхфазного генератора и приёмника треугольником. Основные соотношения. Векторные диаграммы. Сравнение со схемой "звезда с нейтральным проводом".
4. Мощность в трёхфазной цепи. Формулы активной, реактивной и полной мощности симметричного приёмника. Мгновенная мощность симметричного приёмника. Измерение активной мощности.
5. Основы алгебры комплексных чисел. Закон Ома в комплексной форме. Комплексное сопротивление и комплексная проводимость. Эквивалентный переход от последовательной цепи к параллельной и наоборот.
6. Законы Кирхгофа в комплексной форме. Комплексная мощность в цепи синусоидального тока.
7. Топографические векторные диаграммы в комплексной плоскости и принципы их построения.
Содержание
Оформление курсовой работы . . . . . . . . . . . . . . . . . . . . . . . . . 3
Краткие сведения из теории . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Задание на курсовую работу . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Подготовка заданной цепи к расчёту символическим методом . . . . . . . 22
Расчёт цепи при соединении приёмника звездой . . . . . . . . . . . . . . . 25
Расчёт цепи при соединении приёмника треугольником . . . . . . . . . . . 30
Проверка баланса мощностей и сравнение результатов расчёта . . . . . . . 33
Библиографический список . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
Приложение 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Приложение 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
Приложение 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
Дата добавления: 2015-08-01; просмотров: 1312;
