Соединение фаз генератора и приёмника звездой
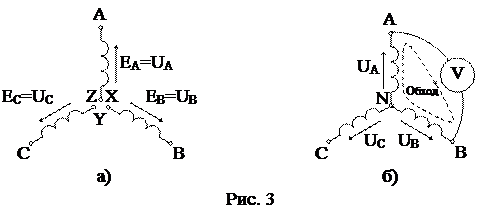 |
На рис. 3а показана схема фаз генератора, подготовленная к соединению звездой. Принцип соединения звездой (рис. 3б) заключается в электрическом соединении концов фаз X, Y, Z в общий электрический узел, называемый нейтральной точкой генератора N. Начала фаз генератора A, B, C подключаются к трём линейным проводам.
При расчёте цепей трёхфазного тока принято считать генератор источником бесконечной мощности, у которого отсутствуют внутренние сопротивления, а следовательно и падения напряжения в них при протекании тока, что позволяет заменить ЭДС соответствующими напряжениями, то есть EmA=UmA, EmB=UmB, EmC=UmC.
На рис. 3 стрелками показаны положительные направления ЭДС (напряжений) в фазах генератора для действующих (среднеквадратических) значений:E= 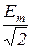 ; U=
; U= 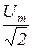 .
.
Фазным напряжением генератора (или приёмника) называется разность электрических потенциалов, то есть напряжение между началом и концом одной и той же фазы генератора (или приёмника).
Линейным напряжением называется напряжение между началами двух разных фаз генератора (или приёмника).
Применительно к генератору, соединённому звездой, фазное напряжение UA – это напряжение (разность потенциалов) между началом фазы A и её концом X (рис. 3а), или между началом фазы A и нейтральной точкой N (рис. 3б), потенциал которой является потенциалом всех трёх концов фаз X, Y, Z.
Как видно из рис. 3б, линейное напряжение UAB представляет собой падение напряжения в вольтметре, подключённом к началам фаз A и B. Применив второй закон Кирхгофа к замкнутому контуру, образованному фазами A-X, B-Y и цепью вольтметра V, получим с учётом направления обхода контура (рис. 3б) 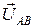 =
= 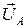 -
- 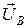 , то есть вектор линейного напряжения
, то есть вектор линейного напряжения 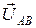 равен геометрической разности векторов соответствующих фазных напряжений (
равен геометрической разности векторов соответствующих фазных напряжений ( 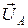 и
и 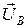 ). Переключив вольтметр на другие пары выходных зажимов генератора, получим
). Переключив вольтметр на другие пары выходных зажимов генератора, получим 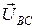 =
= 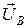 -
- 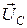 ,
, 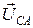 =
= 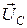 -
- 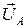 .
.
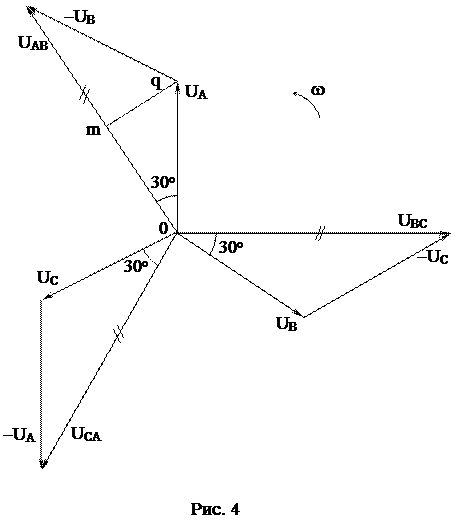
На рис. 4 показана векторная диаграмма напряжений генератора с соответствующими графическими построениями. Как видно из рис. 4, линейные напряжения образуют симметричную звезду векторов (UAB=UBC=UCA=UЛ), которая опережает звезду векторов фазных напряжений на угол 300. Опустив из вершины тупого угла одного из равнобедренных треугольников высоту (которая является и медианой), получим прямоугольный треугольник Dmq0, из которого следуют соотношения: 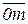 =
= 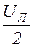 ;
; 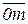 =
= 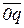 cos300=UФ
cos300=UФ 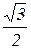 . Приравняв правые части этих равенств, получим UЛ=
. Приравняв правые части этих равенств, получим UЛ= 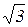 UФ, то есть линейное напряжение генератора, соединённого звездой, в
UФ, то есть линейное напряжение генератора, соединённого звездой, в 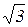 раз больше фазного.
раз больше фазного.
 |
Аналогично генератору соединяется звездой приёмник, то есть концы фаз x, y, z объединяются в нейтральную (нулевую) точку n, а начала a, b, c подключаются к линейным проводам.
На рис. 5 показана электрическая цепь, соединённая звездой, на которой токи, напряжения и сопротивления фаз представлены в виде комплексных чисел.*
Провода (A-a, B-b, C-c), соединяющие начала фаз генератора с началами одноимённых фаз приёмника называются линейными проводами.
|
Сопротивлениями линейных проводов и нейтрального провода в данной курсовой работе будем пренебрегать, поэтому линейные провода будут иметь электрические потенциалы начал одноимённых фаз генератора и приёмника, а нейтральный провод – потенциал концов фаз. С учётом сделанного допущения линейные напряжения можно определить как напряжения между двумя линейными проводами, а фазные напряжения - как напряжения между соответствующими линейными проводами и нейтральным проводом.
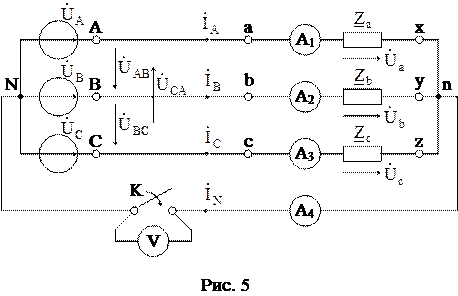
Фазным током генератора (или приёмника) называется ток в фазе генератора (или приёмника).
Линейным током называется ток в линейном проводе. Является очевидным, что при соединении звездой линейные токи равны соответствующим фазным токам (IЛ=IФ). Например, амперметр A1 в схеме на рис. 5 измеряет ток IA, который, не разветвляясь, протекает по фазе A-X генератора, линейному проводу A-a и фазе a-x приёмника.
Ток в нейтральном проводе IN согласно первому закону Кирхгофа равен сумме фазных (линейных) токов (ключ K в схеме на рис. 5 замкнут).
Вектор тока 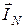 равен геометрической сумме
равен геометрической сумме 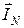 =
= 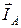 +
+ 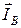 +
+ 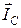 , а комплекс тока
, а комплекс тока 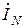 равен алгебраической сумме
равен алгебраической сумме 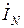 =
= 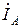 +
+ 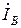 +
+ 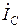 .
.
При симметричной нагрузке ток в нейтральном проводе равен нулю и необходимость в нём отпадает. Поэтому заведомо симметричные приёмники (например, асинхронные и синхронные двигатели при соединении обмоток статора звездой) подключаются к источнику тремя линейными проводами.
Покажем, что при симметричной нагрузке ток в нейтральном проводе отсутствует ( 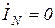 ). Как известно, симметричной нагрузкой является приёмник, у которого равны комплексные сопротивления фаз, то есть
). Как известно, симметричной нагрузкой является приёмник, у которого равны комплексные сопротивления фаз, то есть 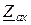 =
= 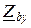 =
= 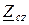 =
= 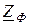 = =zФ e jj=rФ+jxФ. Поскольку сопротивления нейтрального и линейных проводов приняты равными нулю, то симметричная система напряжений с выходных зажимов A, B, C, N генератора накладывается на входные зажимы a, b, c, n приёмника, то есть можно принять:
= =zФ e jj=rФ+jxФ. Поскольку сопротивления нейтрального и линейных проводов приняты равными нулю, то симметричная система напряжений с выходных зажимов A, B, C, N генератора накладывается на входные зажимы a, b, c, n приёмника, то есть можно принять: 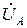 =
= 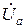 ,
, 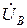 =
= 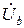 ,
, 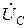 =
= 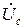 .
.
Согласно закону Ома в комплексной форме фазные (линейные) токи приёмника: 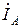 =
= 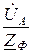 ;
; 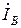 =
= 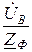 ;
; 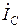 =
= 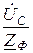 .
.
Ток нейтрального провода: 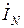 =
= 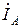 +
+ 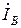 +
+ 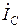 =
= 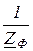 (
( 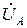 +
+ 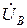 +
+ 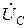 )=0, так как выражение в скобках обращается в нуль.
)=0, так как выражение в скобках обращается в нуль.
При несимметричной нагрузке ток в нейтральном проводе не равен нулю, поэтому при обрыве провода (ключ K в схеме рис. 5 разомкнут) появляется разность электрических потенциалов между нейтральными точками генератора и приёмника, которое называется напряжением смещения нейтрали (UN).
Комплекс действующего значения этого напряжения рассчитывается по формуле:
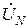 =
= 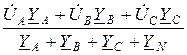 , (1)
, (1)
где 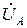 ,
, 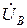 ,
, 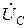 - комплексы фазных напряжений генератора;
- комплексы фазных напряжений генератора;
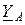 =
= 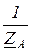 ,
, 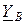 =
=  ,
, 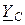 =
= 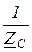 - комплексы проводимостей фаз приёмника;
- комплексы проводимостей фаз приёмника;
 =
= 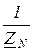 - комплексная проводимость нейтрального провода (
- комплексная проводимость нейтрального провода ( 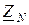 - его комплексное сопротивление).
- его комплексное сопротивление).
При разомкнутом ключе K (рис. 5) можно составить уравнения по второму закону Кирхгофа для трёх замкнутых контуров, образованных каждой из фаз A, B, C трехфазной цепи с измерительной цепью вольтметра V, показывающего величину напряжения смещения нейтрали UN = mod 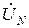 , и получить выражение для фазных напряжений приёмника:
, и получить выражение для фазных напряжений приёмника:
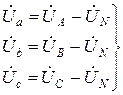 (2)
(2)
Нетрудно убедиться, что вычитание одного и того же вектора 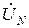 из векторов фазных напряжений генератора
из векторов фазных напряжений генератора 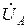 ,
, 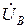 ,
, 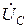 делает систему фазных напряжений приёмника несимметричной, а это приводи к ненормальной работе фаз приёмника.
делает систему фазных напряжений приёмника несимметричной, а это приводи к ненормальной работе фаз приёмника.
При наличии нейтрального провода (ключ K в схеме на рис. 5 замкнут) можно принять 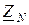 =0, то есть
=0, то есть  =
= 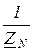 ®¥, вследствие чего правая часть равенства (1) обращается в нуль. Таким образом, при наличии нейтрального провода напряжение смещения нейтрали
®¥, вследствие чего правая часть равенства (1) обращается в нуль. Таким образом, при наличии нейтрального провода напряжение смещения нейтрали 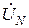 =0, а фазные напряжения приёмника, как это следует из равенств (2),будут равны фазным напряжениям генератора, то есть будут симметричными. Поэтому можно утверждать, что наличие нейтрального провода обеспечивает независимость работы фаз приёмника, поскольку каждая фаза оказывается включённой на одну и ту же величину напряжения.
=0, а фазные напряжения приёмника, как это следует из равенств (2),будут равны фазным напряжениям генератора, то есть будут симметричными. Поэтому можно утверждать, что наличие нейтрального провода обеспечивает независимость работы фаз приёмника, поскольку каждая фаза оказывается включённой на одну и ту же величину напряжения.
Из равенств (1) и (2) также следует, что при отсутствии нейтрального провода (  =0,
=0, 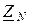 ®¥) и симметричной нагрузке (
®¥) и симметричной нагрузке ( 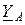 =
= 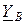 =
= 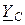 =
= 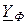 ) напряжение смещения нейтрали
) напряжение смещения нейтрали 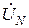 =0, то есть система фазных напряжений приёмника будет также симметричной.
=0, то есть система фазных напряжений приёмника будет также симметричной.
Необходимо обратить внимание на то, что система линейных напряжений всегда остаётся симметричной (даже при обрыве нейтрального провода и несимметричной нагрузке, когда симметрия фазных напряжений приёмника нарушается).
Дата добавления: 2015-08-01; просмотров: 1750;
