Колебательное звено. Колебательным звеном называется звено, связь между выходной и входной величиной которого определяется линейным дифференциальным уравнением второго порядка

Колебательным звеном называется звено, связь между выходной и входной величиной которого определяется линейным дифференциальным уравнением второго порядка вида:

где Т – постоянная времени (сек.)

ξ – относительный коэффициент затухания.

Рассмотрим переходный процесс в таком звене при и

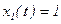
Тогда решением уравнения будет:

,

Где и представляют собой вещественные и мнимые комплексные корни характеристического уравнения

То есть ,

, – постоянные интегрирования, которые определяются из начальных условий при и

Они находятся из соотношений

Из второго уравнения: ,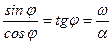

Из первого уравнения: , ,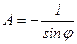

.

Подставим полученные значения в решение уравнения:

,

где – частота колебаний при

Из последнего уравнения видно, что характер изменения во многом зависит от величины .

В операторном виде:

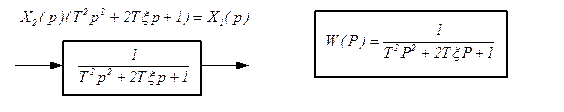
При

Таким образом

; ;

;

, , , , .

, , , , .

, , , , .

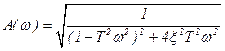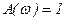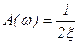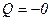Из анализа следует, что ЛАЧХ колебательного звена приблизительно представляется двумя асимптотами, сопрягающимися при , низкочастотные асимптоты являются прямой, совпадающей с осью абсцисс, высокочастотные асимптоты являются прямой с наклоном

5.Передаточные ф-ции и ЧХ при различных соединениях звеньев.(3 стр. 12-14)