Методические указания по выполнению лабораторной работы № 4
В проводной связи для передачи энергии сигналов используются воздушные и кабельные линии. Передача ведется в основном по двухпроводным цепям. Значительно реже применяются однопроводные цепи. При протекании по цепи электрического тока на активном и индуктивном сопротивлениях проводов падает напряжение, а через емкость и проводимость изоляции между проводами или между проводом и землей происходит утечка (ответвление) тока.
Активное сопротивление, индуктивность, емкость и проводимость изоляции распределены равномерно вдоль цепи, поэтому ее принято называть цепью с распределенными параметрами.
| Участок такой цепи нельзя представить в виде эквивалентной схемы, но опыт показывает, что элементарно короткие участки цепей с достаточной точностью можно представить в виде эквивалентных схем, простейшая из которых приведена на рис. 4.1. | 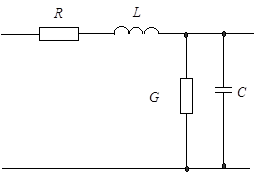
|
| Рис. 4.1. Эквивалентная схема участка цепи |
Схему электрической цепи можно представить в виде ряда таких эквивалентных схем или звеньев, включенных последовательно. Если бы требовалось получить схему, точно соответствующую действительной цепи, то необходимо было бы взять звенья, эквивалентные бесконечно малой длине цепи.
Величины активного сопротивления, индуктивности, емкости и проводимости изоляции 1 км цепи принято называть ее первичными параметрами. Первичными их называют потому, что они влияют на передачу энергии по цепи и от них зависят все остальные характеристики цепи. Первичные параметры имеют следующие обозначения: R - активное сопротивление проводов цепи в омах на километр; L - индуктивность проводов цепи в генри на километр; С - емкость между проводами цепи в фарадах на километр; G - проводимость изоляции между проводами цепи в сименсах на километр.
4.1. Активное сопротивление проводов цепи
Активное сопротивление проводов является важнейшим первичным параметром, так как большая часть потерь мощности в цепи происходит в активном сопротивлении проводов.
При передаче электрической энергии по цепи мощность расходуется как в активном сопротивлении (затрачивается на нагревание проводов) так и в проводимости изоляции между проводами. Потери мощности в проводимости изоляции невелики, и ими обычно можно пренебречь по сравнению с потерями мощности в активном сопротивлении проводов цепи.
Сопротивление проводника при постоянном токе определяется по формуле
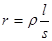 (4.1)
(4.1)
где 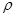 - удельное сопротивление материала проводов при 20°С в (
- удельное сопротивление материала проводов при 20°С в ( 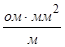 ),
), 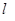 -длина проводника в м, s - сечение проводника, мм2.
-длина проводника в м, s - сечение проводника, мм2.
Формулу для сопротивления 1 км проводов двухпроводной цепи при постоянном токе получим, если подставим 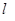 =2000 м и
=2000 м и 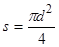
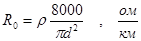 . (4.2)
. (4.2)
При переменном токе активное сопротивление проводов цепи больше, чем при постоянном токе. Увеличение активного сопротивления происходит вследствие наличия переменных магнитных полей, создаваемых переменным током, проходящим по цепи.
При постоянном токе плотность тока по всему сечению провода одинакова. При переменном токе плотность тока по сечению проводника становится неодинаковой: меньше - в центре, больше - у поверхности проводника.
Чем выше частота f переменного тока, чем больше магнитная проницаемость m материала проводов, чем больше диаметр проводов, тем резче проявляется поверхностный эффект. Таким образом, поверхностный эффект приводит к уменьшению полезного сечения проводника т.е. к увеличению его активного сопротивления.
Активное сопротивление проводов цепи с учетом поверхностного эффекта определяется по формуле
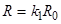 (4.3)
(4.3)
где k1 коэффициент, учитывающий увеличение активного сопротивления вследствие поверхностного эффекта. Коэффициент k1 определяется по таблицам в зависимости от вспомогательной величины X (табл.4.2.)
| Таблица 4.2. Зависимость k1 от X | |||||||
| X | k1 | X | k1 | X | k1 | X | k1 |
| 0,25 | 1,000 | 1,318 | 3,446 | 7,328 | |||
| 0,5 | 1,000 | 3,5 | 1,492 | 9,5 | 3,63 | 9,094 | |
| 1,005 | 1,687 | 3,8 | 10,86 | ||||
| 1,2 | 1,011 | 4,5 | 1,863 | 4,151 | 12,63 | ||
| 1,4 | 1,02 | 2,043 | 4,504 | 14,39 | |||
| 1,6 | 1,033 | 5,5 | 2,22 | 4,856 | 16,16 | ||
| 1,8 | 1,052 | 2,394 | 5,209 | 17,93 | |||
| 1,078 | 6,5 | 2,58 | 5,562 | 20,46 | |||
| 2,2 | 1,111 | 2,743 | 5,915 | 25,00 | |||
| 2,4 | 1,152 | 7,5 | 2,92 | 6,268 | 28,54 | ||
| 2,6 | 1,2 | 3,094 | 6,621 | 32,07 | |||
| 2,8 | 1,256 | 8,5 | 3,28 | 6,974 | 35,61 |
Для двухпроводных цепей величина X определяется по формуле
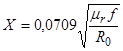 , (4.4)
, (4.4)
где mr - относительная магнитная проницаемость материала проводов (для медных проводов mr =1, для стальных проводов mr = 120); f- частота переменного тока, гц; R0 - сопротивление 1 км двухпроводной цепи при постоянном токе при данной температуре.
Величина Х для воздушных медных цепей может быть вычислена по формуле
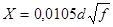 , (4.5)
, (4.5)
а для кабельных цепей с медными жилами по формуле
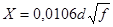 . (4.6)
. (4.6)
Активное сопротивление проводов коаксиальной цепи равно сумме активных сопротивлений внутреннего и внешнего проводов ее и для медных проводов при температуре 20°C определяется по формуле
 , (4.7)
, (4.7)
где d—диаметр внутреннего провода, мм; D — внутренний диаметр внешнего провода, мм.
Таким образом, активное сопротивление проводов коаксиальной цепи обратно пропорционально диаметрам внутреннего и внешнего проводов цепи и с увеличением частоты возрастает пропорционально корню квадратному из частоты.
Биметаллические провода, применяемые на воздушных линиях, конструируются таким образом, что внутри находится цилиндрический стальной провод, а внешним слоем служи медный цилиндр.
Активное сопротивление одного биметаллического провода можно выразить следующей формулой:
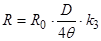 , (4.8)
, (4.8)
где 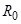 - сопротивление 1 км сплошного медного провода диаметром D, D – внешний диаметр биметаллического провода, мм,
- сопротивление 1 км сплошного медного провода диаметром D, D – внешний диаметр биметаллического провода, мм, 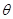 - толщина стенок внешнего медного цилиндра, мм, k3 – коэффициент, учитывающий поверхностный эффект в биметаллическом проводе. Коэффициент k3 определяется по табл. 4.3. в зависимости от коэффициента
- толщина стенок внешнего медного цилиндра, мм, k3 – коэффициент, учитывающий поверхностный эффект в биметаллическом проводе. Коэффициент k3 определяется по табл. 4.3. в зависимости от коэффициента
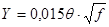 , (4.9)
, (4.9)
где f – частота в Гц.
| Таблица 4.3. Зависимость k3 от Y | |||||
| Y | k3 | Y | k3 | Y | k3 |
| 0,1 | 0,94 | 1,0 | 1,23 | 1,9 | 1,97 |
| 0,2 | 0,97 | 1,1 | 1,28 | 2,0 | 2,06 |
| 0,3 | 1,00 | 1,2 | 1,34 | 2,5 | 2,52 |
| 0,4 | 1,02 | 1,3 | 1,43 | 3,0 | 3,01 |
| 0,5 | 1,04 | 1,4 | 1,52 | 3,5 | 3,5 |
| 0,6 | 1,06 | 1,5 | 1,61 | 4,0 | 4,00 |
| 0,7 | 1,09 | 1,6 | 1,70 | >4,0 | Y |
| 0,8 | 1,13 | 1,7 | 1,79 | ||
| 0,9 | 1,17 | 1,8 | 1,88 |
4.2. Индуктивность проводов цепей связи
Двухпроводную цепь, по которой проходит переменный ток, создающий магнитное поле вокруг каждого провода цепи, можно рассматривать как длинную прямоугольную петлю.
Ее индуктивность является суммой двух величин - внутренней индуктивности и внешней индуктивности. Внутренняя индуктивность связана с магнитным потоком, пересекающим провода цепи, и зависит от материала проводов и от частоты тока. Внешняя индуктивность связана с магнитным потоком, находящимся в пространстве между проводами, и не зависит от материала проводов и частоты тока, а зависит только от диаметра проводов и расстояния между ними.
Дата добавления: 2015-07-30; просмотров: 754;
