Интерпретации в математическом моделировании

Интерпретация (от латинского “interpretatio” — разъяснение, толкование, истолкование) определяется как совокупность значений (смыслов), придаваемых каким-либо образом элементам некоторой системы (теории), например, формулам и отдельным символам. В математическом аспекте интерпретация — это экстраполяция исходных положений какой-либо формальной системы на какую-либо содержательную систему, исходные положения которой определяются независимо от формальной системы. Следовательно, можно утверждать, что интерпретация — это установление соответствия между некоторой формальной и содержательной системами. В тех случаях, когда формальная система оказывается применимой (интер­претируемой) к содержательной системе, т.е. установлено что между элементами формальной системы и элементами содержательной системы существует взаимно однозначное соответствие, все исходные положения формальной системы получают подтверждение в содержательной системе. Интерпретация считается полной, если каждому элементу формальной системы соответствует некоторый элемент (интерпретант) содержательной системы. Если указанное условие нарушается, имеет место частичная интерпретация.

При математическом моделировании в результате интерпретации задаются значения элементов математических выражений (символов, операций, формул) и целостных конструкций.

Основываясь на приведенных общих положениях, определим содержание интерпретации применительно к задаче математического моделирования.

Определение.Интерпретация в математическом моделировании — это информационный процесс преобразования концептуального математического объекта (КМО) в конкретную математическую модель (ММ) конкретного объекта на основе отображения непустого информационного множества данных и знаний, определяемого КМО и называемого областью интерпретации, в кообласть — информационное множество данных и знаний, определяемое предметной областью и объектом моделирования и называемое областью значений интерпретации.

Таким образом, интерпретацию следует рассматривать как один из основополагающих механизмов (инструментов) технологии математического (научного) моделирования.

Именно интерпретация, придавая смысл и значения элементам (компонентам) математического выражения, делает последнее математической моделью реального объекта.

Виды и уровни интерпретаций. Создание математической модели системного элемента — многоэтапный процесс. Основным фактором, определяющим этапы перехода от КМО к ММ, является интерпретация. Количество этапов и их содержание зависит от начального (исходного) информационного содержания интерпретируемого математического объекта — математического описания и требуемого конечного информационного содержания математического объекта — модели. Полный спектр этапов интерпретации, отражающий переход от КМО — описания к конкретной ММ, включает четыре вида интерпретаций: синтаксическую (структурную), семантическую (смысловую), качественную (характеристическую) и количественную (численную). В общем случае, каждый из перечисленных видов интерпретации может иметь многоуровневую реализацию. Рассмотрим более подробно перечисленные виды интерпретаций.

Cинтаксическая интерпретация.Синтаксическую интер­пре­тацию будем рассматривать как отображение морфо­логической (структурной) организации исходного КМО в морфологическую организацию структуру заданного (или требуемого) КМО. Синтаксическая интерпретация может осуществляться как в рамках одного математического языка, так и различных математических языков.

При синтаксической интерпретации КМО возможны несколько вариантов задач реализации.

Задача 1. Пусть исходный КМО не структурирован, например, задан кортежем элементов. Требуется посредством синтаксической интерпретации сформировать морфо­логи­ческую структуру математического выражения

. (1)

Задача 2.Пусть КМО имеет некоторую исходную морфологическую структуру, которая по тем или иным причинам не удовлетворяет требованиям исследователя (эксперта). Требуется в соответствии с целями и задачами моделирования, посредством синтаксической интерпретации, преобразовать исходную структуру 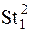в адекватную требуемую 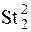, т.е.

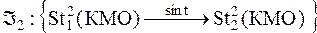. (2)

Задача 3.Пусть КМО имеет некоторую исходную морфологическую структуру 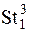, удовлетворяющую общим принципам и требованиям исследователя с точки зрения её синтаксической организации. Требуется посредством синтаксической интерпретации конкретизировать КМО со структурой 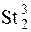до уровня требований, определяемых целями и задачами моделирования

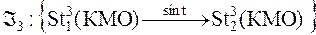. (3)

Таким образом, синтаксическая интерпретация математических объектов даёт возможность формировать морфологические структуры КМО, осуществлять отображение (трансли­ровать) морфологические структуры КМО с одного математического языка на другой, конкретизировать или абстрагировать морфологические структурные представления КМО в рамках одного математического языка.

Семантическая интерпретация. Семантическая интерпретация предполагает задание смысла математических выражений, формул, конструкций, а также отдельных символов и знаков в терминах сферы, предметной области и объекта моделирования. Семантическая интерпретация даёт возможность сформировать по смысловым признакам однородные группы, виды, классы и типы объектов моделирования. В зависимости от уровней обобщения и абстрагирования или, наоборот, дифференциации и конкретизации, семантическая интерпретация представляется как многоуровневый, многоэтапный процесс.

Таким образом, семантическая интерпретация, задавая смысл концептуальному математическому объекту, “переводит” последний в категорию математической модели объекта-оригинала, в терминах которого и осуществляется такая интерпретация.

Качественная интерпретация. Интерпретация на качественном уровне предполагает существование качественных параметров и характеристик объекта-оригинала, в терминах (значениях) которых и производится интерпретация. При качественной интерпретации могут использоваться графические и числовые представления, посредством которых, например, интерпретируется режим функционирования объекта моделирования.

Количественная интерпретация. Количественная интерпретация осуществляется за счет включения в рассмотрение количественных целочисленных и рациональных величин, определяющих значения констант, параметров, характеристик и т.п.

В результате количественной интерпретации появляется возможность из класса, группы или совокупности аналогичных математических объектов выделить один единственный, являющийся конкретной математической моделью конкретного объекта-оригинала.

Таким образом, в результате четырех видов интерпретаций — синтаксической, семантической, качественной и количественной происходит поэтапная трансформация КМО, например, концептуальной метамодели (КММ) функциональной системы 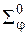, в конкретную математическую модель конкретного объекта моделирования.

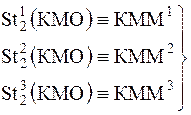. (4)

Контрольные вопросы

1. Дайте описание этапа первичной математической обработки эмпирических данных.

2. Дайте описание этапа, математического моделирования.

3. Дайте описание этапа относительно полной математической теории.

4. Дайте определение математического моделирования.

5. Дайте определение математической модели.

6. Укажите основной фактор, определяющий этапы перехода от КМО к КММ. Дайте его определение.

7. Дайте определение полной и частичной интерпретации.

8. Перечислите виды интерпретации.

9. Дайте определение синтаксической интерпретации.

10. Приведите 3 возможные варианта задач реализации при синтаксической интерпрета­ции КМО.

11. Дайте определение семантической интерпретации.

12. Дайте определение качественной интерпретации.

13. Дайте определение количественной интерпретации.