Определение моментов инерции сложных тел методом колебания

Упругая проволока ОО₁ совпадая с осью вращения, в данном случае ось О-О₁ нашего барабана.

Закручивают нить и опускают. Получают крутильные колебания.

Для крутильных колебаний имеем дифференциальное уравнение:

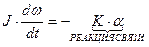; (1)

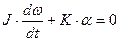, (2)

где J- момент инерции тела относительно оси вращения О-О₁;

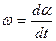(угловая скорость); (3)

(угловое ускорение). (4)

Имеющимися сопротивлениями (воздуха, внутреннего трения) пренебрегаем. Дело в том, что мы ищем частоту колебания. А внешние силы оказывают малое влияние, Поэтому мы имеем такое дифференциальное уравнение.

Решение дифференциального уравнения:

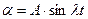, (5)

где 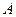- амплитуда;

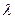- круговая частота;

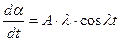; (6)

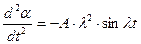; (7)

Подставив (7) в (2) мы должны получить тождество:

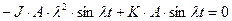; (8)

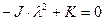; (9)

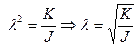; (10)

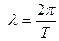; (11)

Подставим (11) в (10), получим:

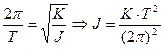, (12)

где K- коэффициент жёсткости нашей проволоки.

Поэтому нам необходимо найти “K” .

Порядок определения момента инерции тела:

1. Подвешиваем тело с известным моментом инерции J₁:

На основании формулы (12) находим “K”:

.

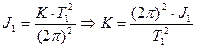1. Подвешиваем тело с неизвестным моментом инерции J_x и на основании (12) записываем:

;

;

.

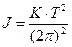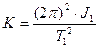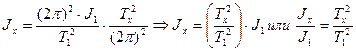Это экспериментальный способ.