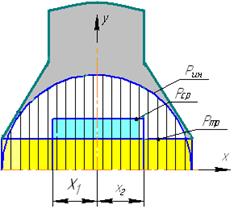
Высота режущей кромки
Высота режущей кромки сегмента h может быть определена из условия полного среза стеблей на расстоянии Vм t1ход за один ход ножа . При этом сегмент срежет стебли на расстоянии 2h. Подачей на нож называется расстояние,
| |
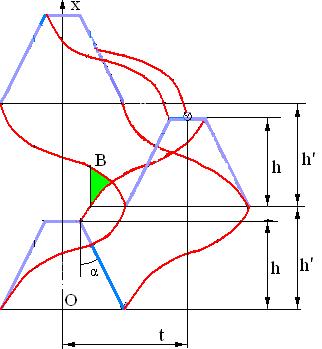
sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
sin(α – β) = sinαcosβ – cosαsinβ
cos(α – β) = cosαcosβ + sinαsinβ
Лекция 3.
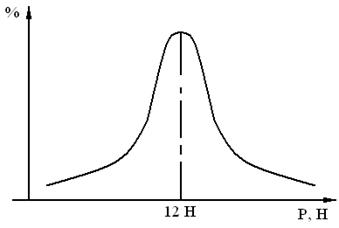
3.1. ОБЩАЯ ХАРАКТЕРИСТИКА ФИЗИКО-МЕХАНИЧЕСКИХ СВОЙСТВ СТЕБЛЕЙ ТРАВ И ХЛЕБНЫХ ЗЛАКОВ.
Уборку скашиванием производят для многих культур. Наиболее характерные из них - колосовые зерновые и толстостебельные, травы. Лучшими для трав являются такие сроки кошения, которые позволяют получить сено с высоким содержанием питательных веществ: протеина и каротина. Для злаковых трав — это период колошения (до начала цветения); для бобовых — период бутонизации; для естественных трав — период начала цветения. Заканчивать кошение трав следует до наступления периода полного цветения.
При очень низком срезе трав снижается их способность к воспроизводству, при высоком — теряется значительная часть урожая. В лесолуговой зоне высота среза естественных сенокосов — 5—6 см, в степной — 4 см. Высота среза сеяных трав — 8—10 см.
Высота трав в среднем составляет 40—80 см; для пшеницы и ржи — 100—170 см. Урожайность трав (по сену) в зависимости от зоны — 5—30 ц/га. Среднее число стеблей на 1 м2 составляет для ржи, озимой и яровой пшеницы 450— 600, для естественных трав 1170—4845.
Коэффициент трения стеблей пшеницы при влажности 6…50%
f =0,25…0,6; для трав при влажности 60…80% f =0,5…1,48
Плотность материала соломы несколько выше воды.
Жесткость стеблей трав EJ = 49-646 МПа. Модуль упругости сухих стеблей пшеницы Е — 4,67 -7,48 ГПа (2500…5950 кгс/мм2). Растение вплоть до разрыва не образует площадку пластичности (рис. 3.1.)
Работа, затрачиваемая на срезание стеблей с площади 1м2, по данным Г. Д. Терскова, для зерновых равна 98—196 Дж/м2, для трав 196—294 Дж/м2. Работа, необходимая для срезания одного стебля, по данным акад. Л. А. Карпенко, составляет для зрелой ржи 2,26 Дж/с, для зеленой ржи 1,71 Дж/с. Среднее усилие для срезания одного стебля пшеницы равно 1,96—5,88 Н (0,2—0,6 кгс), максимальное достигает 19,6 Н (2 кгс). Тяговое усилие, отнесенное к 1 м захвата режущего аппарата, составляет для зерновых 392—490 Н/м (40— 50 кгс/м), для трав 590—685 Н/м (60—70 кгс/м).
|
Рис.3.1. Вероятностный характер распределения усилия разрыва стеблей
3.2. УПРУГО-ВЯЗКИЕ СВОЙСТВА РАСТЕНИЙ
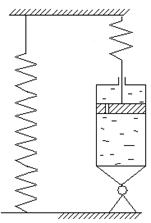
Стебли растений обладают одновременно упругими и вязкими свойствами. Эти свойства можно представить схематично в виде поршня с цилиндром.

Рис 3.2. Механическая модель
упруго-вязких свойств растений
|
Это линейное уравнение с разделяющимися переменными
|
|
|
|
|
Пропотенцируем и получим
|
Умножим на коэфф. К →
Построим график во времени величины 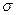
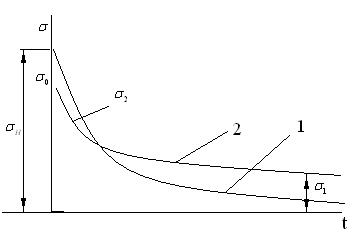
Рис.3.3. Изменение напряжений во времени
для простого (1) упругодемпфирующего звена и для
приближенного к реальности
|
В действительности график 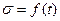 приближен к кривой 2 (рис 2.2.) с более выраженными упругими свойствами. Упруговязкие свойства растений объясняются тем, что помимо обычных упругих тканей в растении есть полости, заполненные воздухом и жидкостью, выход их из которых аналогичен перетоку жидкости в гидроцилиндре. Точные зависимости для конкретных растений до сих пор не установлены и при расчетах пользуются экспериментальными данными, имеющимися в справочной литературе /1,2/
приближен к кривой 2 (рис 2.2.) с более выраженными упругими свойствами. Упруговязкие свойства растений объясняются тем, что помимо обычных упругих тканей в растении есть полости, заполненные воздухом и жидкостью, выход их из которых аналогичен перетоку жидкости в гидроцилиндре. Точные зависимости для конкретных растений до сих пор не установлены и при расчетах пользуются экспериментальными данными, имеющимися в справочной литературе /1,2/
Закон Барба –Кика
Тела из одинакового материала, находящихся под воздействием сходственно распределенных сил работают с равными коэффициентами нагруженности в том случае, если величины внешних сил относятся как квадраты сходственных линейных размеров.
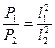 , например
, например 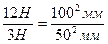
Этот закон применительно к растениям соблюдается статистически (см. рис. 3.1)
|
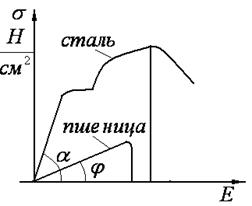
Рис. 3.5. Нагрузочные
характеристики стеблей
Вопросы для контроля.
3.1. Назовите оптимальные стали развития растений для кошения.
3.2. Почему определенные сроки развития для растений являются оптимальные для кошения
3.3. Чем определяется (обуславливается) высота скашивания растений?
3.4. Какая густота стеблей при уборке пшеницы, трав?
3.5. Изобразите графически характер распределения усилия разрыва стеблей
3.6. Изобразите механическую модель упруго-вязких свойств растений
3.7. Чем определяются упруго-пластические свойства стеблей растений
3.8. Запишите выражения для усилия пружины, и усилие поршня:
3.9. Запишите дифф. уравнение поршня при перемещении (для модели)
|
3.11. Что выражает приведенное уравнение
Лекция 4. РЕЗАНИЕ СТЕБЛЕЙ РАСТЕНИЙ.
Так как 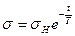 при t = 0 имеем
при t = 0 имеем 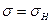 (4.1)
(4.1)
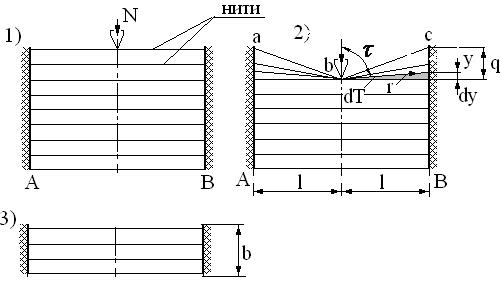
Рис. 4.1. Схема резания под действием нормальной силы Т
Схема стебля при резании представляет собой две стенки, между которыми натянуты нити (рис.4.1.1).
- Определим направление 1-й нити abc.
При резании ввиду краткого промежутка времени t =0 → (4.1)
- Напряжение в нити равняется
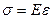 , где
, где 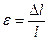 - относительное удлинение. (4.2)
- относительное удлинение. (4.2)
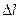 = bc - l , bc =
= bc - l , bc = 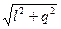 ,
,
где q – глубина погружения ножа (рис.4.1.2).
Тогда
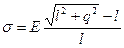 .
.
Преобразуем и определим q
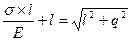 ,
,
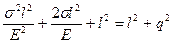 ,
,
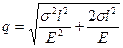 = l
= l  (так как
(так как 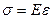 ).
).
В момент погружения на величину разрыва стебля qb (рис.4.1.3):
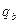 = l
= l 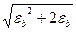 .
.
Вычислим усилие N, необходимое для погружения ножа на величину 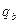 .
.
Рассмотрим участок dy, найдем усилие dT = 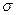 dF (размерность
dF (размерность 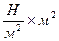 ),
),
где dF = bdy
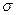 =
= 
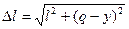 - l (см.(4.2)).
- l (см.(4.2)).
Подставим в dT → dT = 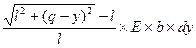 .
.
Из параллелограмма элементарных сил (рис. 4.2)→
|
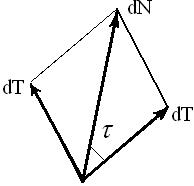
Рис. 4.2. Векторное суммирование
элементарных сил.
Вынесем в выражении (4.3) (q - y)dy за квадратные скобки и обозначим оставшееся выражение как А:
А = 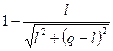 , которое не зависит от переменной y и поэтому как постоянную величину можно вынести из под интеграла.
, которое не зависит от переменной y и поэтому как постоянную величину можно вынести из под интеграла.
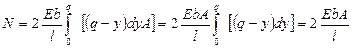 │
│ 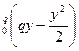 =
=

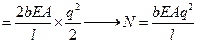 (4.4)
(4.4)
Величина N необходима для погружения ножа на глубину q, если нож движется достаточно быстро.
При подстановке в формулу (4.4) qb вместо q получим усилие N в момент разрыва.
Усилие N - это усилие резания в первой фазе резания. Вторая фаза соответствует случаю, когда на боковые грани ножа действуют силы давления со стороны разрезаемого стебля.
При подстановке значения q в формулу для N видно, что усилие N пропорционально длине отрезка, т.е. чем больше участок резания, тем больше усилие.
Вторая фаза резания – движение лезвия в стебле растения
|
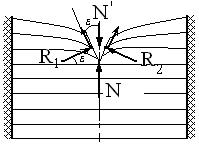
Рис 4.3. Схема сил при движении
ножа в стебле (в плоскости)
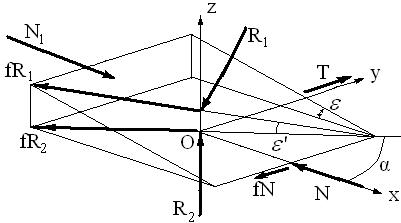
Рис 4.3. Схема сил при движении ножа в стебле со скольжением
1-й случай – резание без скольжения.
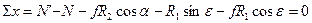 (4.5)
(4.5)
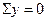
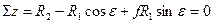 (4.6)
(4.6)
Из (4.6) R2 = R1 (cos  –f sin
–f sin  ) →(4.4)→
) →(4.4)→
N’ = N +R1 f (cos  –f sin
–f sin  )cosα +sin
)cosα +sin  +fcos
+fcos 
N’ = N +R1 (f cos  cosα –f2 sin
cosα –f2 sin  cosα +sin
cosα +sin  +2fcos
+2fcos  )
)
N’ = N +R1 (f cos  cosα –f2 sin
cosα –f2 sin  cosα +sin
cosα +sin  +2fcos
+2fcos  )
)
Без скольжения α→ 0 сos α =1, Величина f2 sin  cosα большего порядка малости
cosα большего порядка малости
N’ = N +R1 (f cos  +sin
+sin  +fcos
+fcos  ) = N +R1 (sin
) = N +R1 (sin  +2fcos
+2fcos  )
)
2-й случай – резание со скольжением.
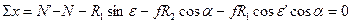
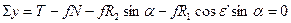
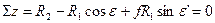
Силы трения в этом случае лежат в плоскости АОZ. Из рис 4.3. по правилу проекций
tg  ’= tg
’= tg  cosα
cosα
R2 = R1 (cos  –f sin
–f sin  ’)
’)
Nc’ = Nc +R1 [sin  –f cosα (cos
–f cosα (cos  ’+cos
’+cos  )]
)]
α→ π/2 тогда cosα→0 и Nc’ ≈ Nc +R1 sin 
|
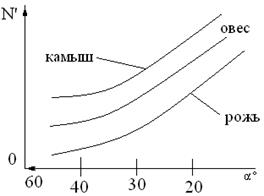
Рис 4.4.
Рассмотрим 2 основные схемы среза растений.
|
|
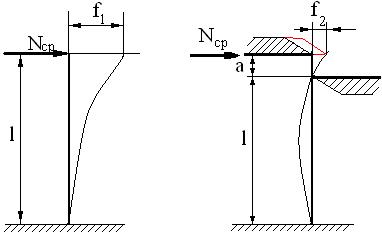
Рис. 4.5. Срез без подпора Рис. 4.6. Срез с подпором
Для среза растения всегда необходимо чтобы:
Nср < Pизг + Pин
Но ввиду того, что масса стебля незначительная для предварительного рассмотрения
Pин= 0.
Выразим Nср для первого и второго случая:
Nср1= 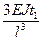 Nср2=
Nср2= 
Очевидно Nср1< Nср2
Лучше производить резание с подпором. При резании трав (с малым значением жесткости ЕJ стеблей) необходимо уменьшать величину зазора «а» между режущими кромками. Это приводит к возрастанию усилия на отгиб и обеспечение нормального процесса резания гибких трав.
Лекция 5
5.1. ТИПЫ РЕЖУЩИХ АППАРАТОВ
В зависимости от соотношения между ходом ножа S, шагом режущей части t (расстояние между осями сегментов) и противорежущей части t0 (расстояние между осями пальцев) различают 4 типа режущих аппаратов сегментного типа с возвратно-поступательным движением ножа:
- аппараты нормального резания с одинарным пробегом сегментов – S = t = t0 (рис. 5.1-а), нормального резания с двойным пробегом сегментов – S = 2t = 2t0 (рис. 5.1-б);
- аппараты среднего резания – S = t = (4/3…5/4) t0 (рис. 5.1-г);
- аппараты низкого резания – S = t = 2t0 (рис. 5.1-в);
- беспальцевые аппараты с двумя подвижными ножами с одинарным – S = t/2 (рис. 5.1-д) и двойным пробегом ножа – S = t
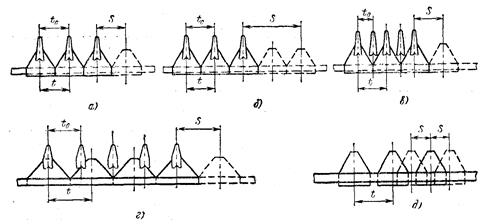
Рис. 5.1. Типы режущих аппаратов
S – ход ножа; t – шаг режущей части (расстояние между осями сегментов); t0 – шаг противорежущей части (расстояние между осями пальцев)
Лучшим аппаратом для косилок и зерновых уборочных машин по качеству резания, меньшим инерционным усилиям, расходу мощности на резание, суммарной нагрузке на лезвия сегмента, а также по эксплуатационной надежности является аппарат нормального резания с одинарным пробегом сегментов. Наиболее часто t =3’=76,2 мм.
Преимущество режущего аппарата с двойным пробегом сегментов состоит в том, что допускаемая подача на один ход ножа больше в 1,5—2 раза, чем у аппарата с одинарным пробегом сегментов. Но данный аппарат имеет и существенные недостатки: 1) недостаточное использование максимальной скорости ножа в процессе срезания стеблей не позволяет с увеличением радиуса кривошипа в 2 раза уменьшить на столько же и частоту вращения; 2) колебания пальцевого бруса, рамы машины при двойном ходе ножа значительно больше, чем при одинарном; 3) при кривошипном приводе ножа в опасном сечении спинки ножа возникают большие напряжения; 4) повреждение лезвий сегментов происходит быстрее, чем в аппаратах с одинарным пробегом сегментов.
Аппараты среднего резания применяются на машинах с большим захватом, так как скорость резания меньше уменьшается в конце защемления, а силы инерции не увеличиваются.
Беспальцевый режущий аппарат с двумя подвижными ножами применяют при уборке урожая в самых тяжелых условиях: при уборке трав, спутанного и полегшего хлеба, риса, бобовых культур, где обычно режущие аппараты с пальцами работать не могут, а также при переходе на повышенные поступательные скорости работы жаток. Параметры аппарата могут быть следующие: для косилок S = t/2 = 40 мм, для рисовых жаток S = t/2 = 50 мм.
|

Рис.5.2. Схема для анализа кинематики ножа
Из (5.1)→  , тогда
, тогда 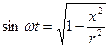 (5.4)
(5.4)
Подставляем (5.4) в (5.2)
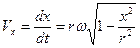
Возведем в квадрат

Разделим на 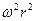 →
→
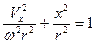
Так как 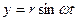 , то y =
, то y =  =
= 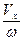 и
и
 - ур-е окружности → y2 + x2 = r2 .
- ур-е окружности → y2 + x2 = r2 .
Отрезок АВ (рис 5.2) в масштабе 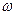 представляет собой величину скорости ножа вдоль оси х. Штриховая окружность – график скорости ножа.
представляет собой величину скорости ножа вдоль оси х. Штриховая окружность – график скорости ножа.
Находим ускорение ножа как функцию перемещения х:
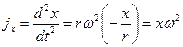
х может принимать значение +r и -r
|
|
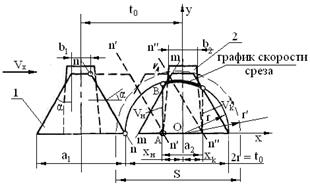
Рис.5.3. Определение скорости резания. 1
– сегмент; 2 – противорежущая пластина.
S = 2r’ > 2r → Это режущие аппараты с перебегом ножа, которые дают качественно лучший срез, но при этом возрастает сила инерции.
Режущий аппарат нормального типа выполняет резание со скольжением, чем > α, тем больше скольжение, но при большом значении может происходить выталкивание стеблей.
5.2. ТРАЕКТОРИЯ ДВИЖЕНИЯ СЕГМЕНТА В ПРОЕКЦИИ НА ГОРИЗОНТАЛЬНУЮ ПЛОСКОСТЬ.
Для графического построения разбиваем дугу на n, например, 8 частей, делим путь h на столько же частей. По траектории можно установить, на каких площадках стебли не подвергаются резанию и их уменьшить.
|
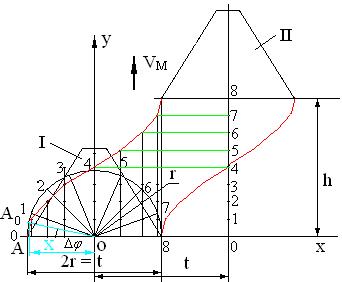
Рис. 5.4. Схема для построения траектории ножа
За время 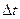 :
:
АА1 = VM 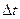
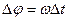
Точка А перейдет в А1 .
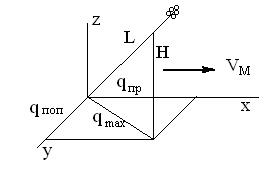
5.3.ОТГИБ СТЕБЛЕЙ
|
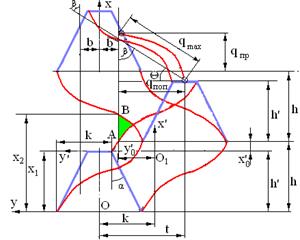
Рис. . 5.5. Схема для определения отгиба
стеблей
параметрическое уравнение косинусоиды
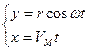 (5.5)
(5.5)
Из 2-го ур-я (5.5)→t = 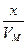 , тогда у = r cos (
, тогда у = r cos ( 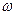
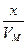 ) (5.6)
) (5.6)
 →
→ 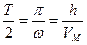 →
→  - подставляем в (5.6)
- подставляем в (5.6)
2. Находим х2
у = r cos ( 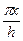 ) – уравнение косинусоиды.
) – уравнение косинусоиды.
tg β = 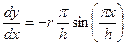
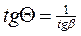
При х = 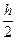 tg βmax =
tg βmax = 
|
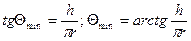
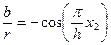
По ф-ле для дополнительных углов
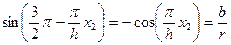 →
→ 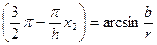 →
→
x2 = 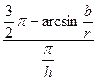 =
= 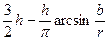
- Находим х1.
Для нахождения перейдем к другим осям координат х’О’у’.
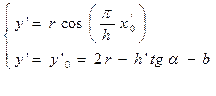 пусть
пусть 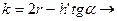
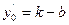
x1 = h’ + x0’
2r – h tgα – b = r cos 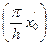 → x0’ =
→ x0’ = 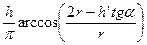
x1 = 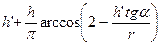
Тогда
qпр = 
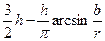 -
- 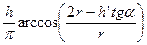
Из выражения продольного и поперечного отгиба можно найти рациональные параметры режущего аппарата. Такими параметрами являются высота сегмента h , угол наклона лезвия α, ход ножа r.
ЛЕКЦИЯ 6.
6.1.СКОЛЬЖЕНИЕ СТЕБЛЯ ПО ЛЕЗВИЮ (до защемления)
Для упрощения рассмотрения рассмотрим статические условия возможности и невозможности скольжения.
Условие скольжения к нижнему основанию
|
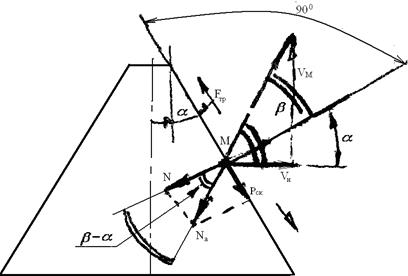
Рис 7.1. Схема действующих сил
Стебли отклоняются в сторону скорости VМ
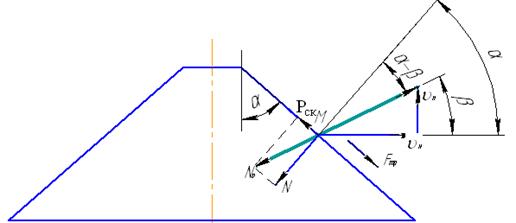
Nа – упругая реакция стебля на сегмент. Скольжение будет в том случае, если:
Рск = Nа ×sin (β -α)≥ Fтр ,
где Fтр= Nа ×соs (β -α) tgφ
φ – угол трения.
Nа ×sin (β -α)≥ Nа ×соs (β -α) tgφ – условие скольжения стебля
→ tg(β -α)≥ tgφ
β ≥ φ + α но и tg β ≥ tg (φ + α) (7.3)
tg β подставляем из (7.1) используя значения (7.2):
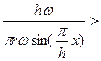 tg (φ + α) сокращаем в левой части
tg (φ + α) сокращаем в левой части 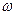 и определяем h:
и определяем h:
h = 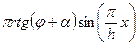 ,
,
где h – подача ножа.
Выражение (7.3) определяет условие постоянного скольжения стебля и должно выполняться даже при β мин, соответствующее VНmax при sin 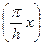 = 1 (см. (7.2)), тогда (7.3)
= 1 (см. (7.2)), тогда (7.3)
преобразуется:
tg βmin = 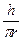 →
→ 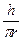 > tg (φ + α) → h >
> tg (φ + α) → h > 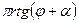 (7.4)
(7.4)
Чтобы происходило скольжение необходимо, чтобы подача h за один полуоборот кривошипа была больше чем правая часть (7.4), а значит α должен быть мал.
6.2. ВОЗМОЖНОСТЬ СКОЛЬЖЕНИЯ К ВЕРХНЕМУ ОСНОВАНИЮ.
Это скольжение опасно, так как возможно выскакивание стебля из под ножа аппарата и стебель не перережется.
Условие скольжения: 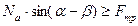
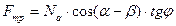
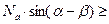
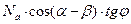
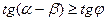

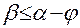 - условие скольжения стебля к верхнему основанию. Это условие не должно выполняться.
- условие скольжения стебля к верхнему основанию. Это условие не должно выполняться.
При больших 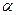 и малых углах
и малых углах  , а также при малых подачах h, которые приводят к малым значениям
, а также при малых подачах h, которые приводят к малым значениям  .
.
6.3. СКОЛЬЖЕНИЕ СТЕБЛЯ ПРИ ЗАЩЕМЛЕНИИ ЕГО МЕЖДУ ЛЕЗВИЯМИ СЕГМЕНТА И ВКЛАДЫША.
Рассмотрим скольжение стебля при возможности защемления
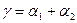


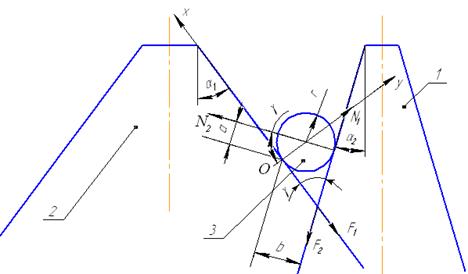
1. Нож; 2. Сегмент; 3. Стебель
Для того чтобы было равновесие стебля в растворе между лезвиями необходимо, чтобы суммы проекций на оси Х и У были равны 0 и суммы моментов относительно произвольной точки O для сил, действующих на стебель были равны 0.
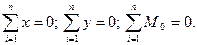
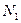 и
и 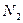 - нормальные реакции, действующие со стороны лезвия на стебель.
- нормальные реакции, действующие со стороны лезвия на стебель.
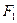 и
и  - силы трения, предупреждающие выскальзывание.
- силы трения, предупреждающие выскальзывание.
r- радиус стебля.
При каких значениях угла  будут обеспечены условия равновесия (его не выскальзывание).
будут обеспечены условия равновесия (его не выскальзывание).
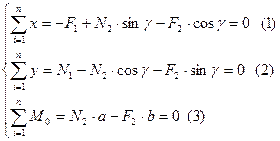
Вместо 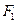 и
и  в (1) подставим их значения:
в (1) подставим их значения:
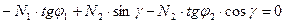
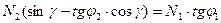 (1)
(1)
Вместо  в (2) подставим его значение:
в (2) подставим его значение:
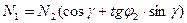 (2)
(2)
Приравнивая уравнения (1) и (2) и домножив обе части на 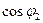 , получим:
, получим:
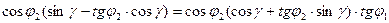
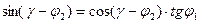

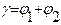 - 1 условие.
- 1 условие.
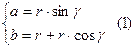
Подставим уравнение (1) в сумму моментов (3):
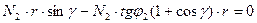
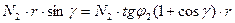
Умножим на 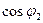 и получим:
и получим:
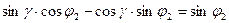
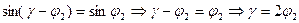
 - 2 условие.
- 2 условие.
Если  , то оба условия дают
, то оба условия дают 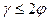 - условие статики.
- условие статики.
ЛЕКЦИЯ 7.
7.1. ПЛОЩАДЬ ПОДАЧИ И НАГРУЗКА НА ЛЕЗВИЕ СЕГМЕНТА РЕЖУЩЕГО АППАРАТА.
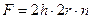
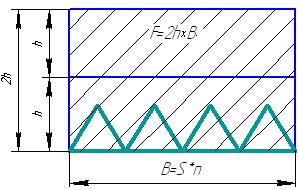
Площадь, скошенная одним сегментом:
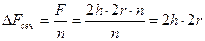
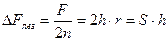 ,
,
где S- ход ножа;
n- число сегментов;
h- подача.
Площадка, описанная точкой О1 по площади 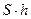 (синусоидальный
(синусоидальный 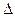 ).
).
Уточним. Запишем уравнение косинусоиды см. (5.6):
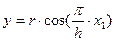 .
.
Перенесём ось ОХ на величину r влево в т.О1:
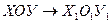
Тогда: 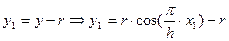 .
.
Обозначим заштрихованную площадку- 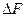 .
.
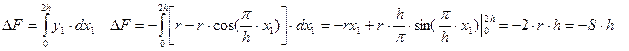
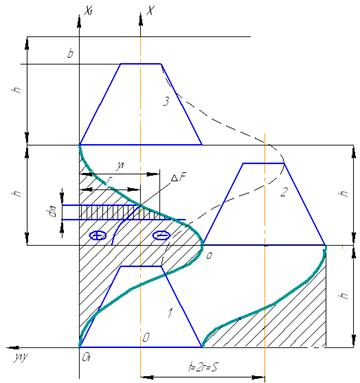
Рис 7.2. К определению площади срезаемой одним лезвием
Эта площадка равна площади, срезаемой одним лезвием.
7.2. РЕЖУЩИЙ АППАРАТ НИЗКОГО РЕЗАНИЯ.
Нагрузка в аппаратах низкого резания на каждый из пальцев будет различной.
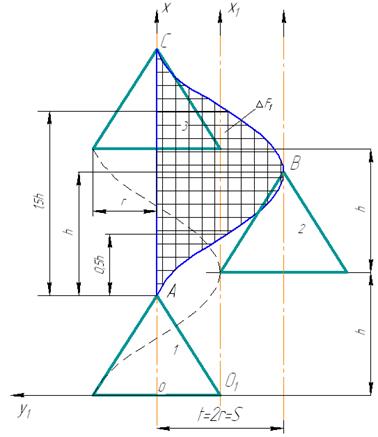
Для режущего аппарата низкого резания имеем:
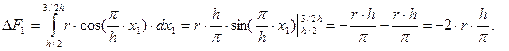
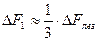 .
.
Количество стеблей, срезаемое у пальца: 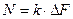 ,
,
где  - коэффициент, показывающий степень густоты расположения стеблей на 1 кв.м.
- коэффициент, показывающий степень густоты расположения стеблей на 1 кв.м. 
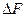 - срезаемая площадка.
- срезаемая площадка.
7.3. СОПРОТИВЛЕНИЕ В РЕЖУЩЕМ АППАРАТЕ.
Нагрузка на спинку ножа приходится от следующих усилий:
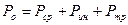 ,
,
где  - усилие от среза стеблей сегментами режущего аппарата (среднее значение);
- усилие от среза стеблей сегментами режущего аппарата (среднее значение);
 - усилие, связанное с ускорением массы ножа;
- усилие, связанное с ускорением массы ножа;
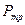 - усилие трения, обусловленное весом ножа и действием прижимов на спинку ножа.
- усилие трения, обусловленное весом ножа и действием прижимов на спинку ножа.
1) 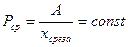 ,
,
где 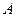 ср- работа среза травы или стеблей за один полуоборот кривошипа;
ср- работа среза травы или стеблей за один полуоборот кривошипа;
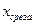 - путь сегмента в процессе от начала резания лезвия до конца резания.
- путь сегмента в процессе от начала резания лезвия до конца резания.
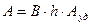 ,
,
где 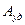 - работа среза 1 м2 травы или стеблей (даётся в справочниках).
- работа среза 1 м2 травы или стеблей (даётся в справочниках).
2) 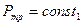 . Оно несколько выше силы трения, так как есть сцепление и другие факторы.
. Оно несколько выше силы трения, так как есть сцепление и другие факторы.
3) 
Заметим, что х во вращательном движении изменяется по синусоидальному закону
Если нам известны  ,
,  ,
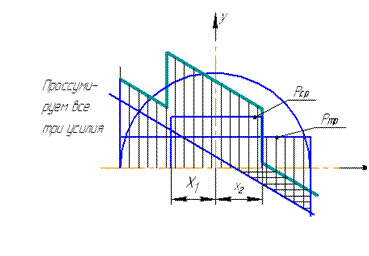
, 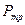 , то можем построить график
, то можем построить график 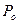 .
.
Заштрихованный график - есть график общего усилия ножа 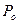 .
.
|
За счёт сил инерции мы имеем два максимума положительный и отрицательный (показана первая половина)
За счёт сил инерции мы имеем два максимума положительный и отрицательный (показана первая половина)
Л8.
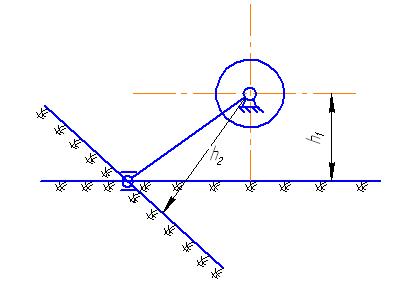
ЛЕКЦИЯ 8.КРИВОШИПНО-ШАТУННЫЙ МЕХАНИЗМ ДЛЯ ПРИВОДА РЕЖУЩЕГО АППАРАТА
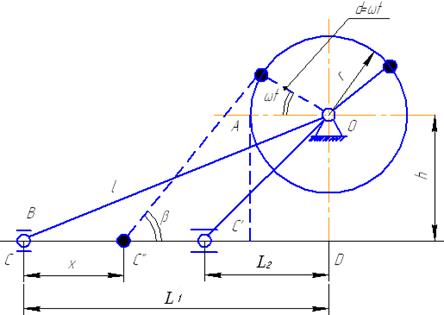
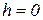 - механизм аксиальный;
- механизм аксиальный;
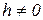 - механизм дизаксиальный;
- механизм дизаксиальный;
h – дизаксиал;
r – радиус кривошипа;
АВ – шатун;
С – ползун (нож режущего аппарата);
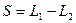 - ход ножа.
- ход ножа.
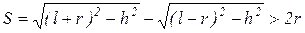 → Величина хода
→ Величина хода 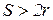
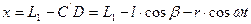
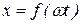 нас интересует х, как функция
нас интересует х, как функция 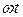
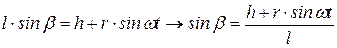
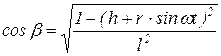

Запишем этот корень как функцию и разложим в ряд Тейлора
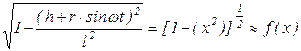
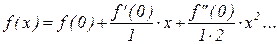
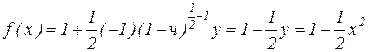

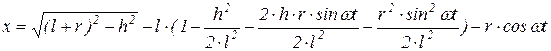
Умножим на – l
1. 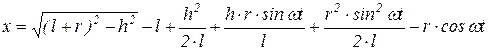
Это выражение показывает, что движение не является синусоидальным, а более сложным. Возьмем производную 
2. 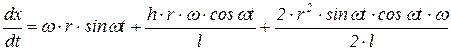

3. 
1 – путь; 2 – скорость; 3 – ускорение.
Если в уравнениях (1,2,3) дать h=0, полученное движение аксиального механизма, если положение h=0, а 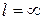 , то получим закон для движения ножа.
, то получим закон для движения ножа.
1-2-3 – общие формулы движения ножа, из которого можно получить любые частные формулы.
Дата добавления: 2015-07-30; просмотров: 1999;

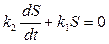
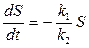
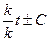
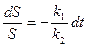
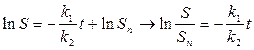


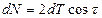
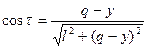 (см. рис.4.1-2)
(см. рис.4.1-2)

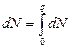
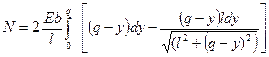 (4.3.)?
(4.3.)?
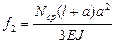
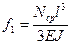
 Параметрическое уравнение пути по оси х и y:
х = -
Параметрическое уравнение пути по оси х и y:
х = - 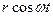 , y = r sin
, y = r sin 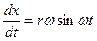 (5.2)
Ускорения:
(5.2)
Ускорения:
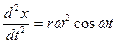 (5.3)
(5.3)
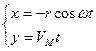 Где t – параметр
Т =
Где t – параметр
Т = 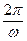 Где Т – период вращения
За
Где Т – период вращения
За 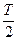 мы пройдем вперед:
Путь машины: h = VM
мы пройдем вперед:
Путь машины: h = VM 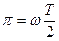
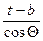 1.Для определения ﮮ
1.Для определения ﮮ 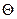 решим
решим
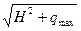 x2 –x1 = qпр
Определим х2
x2 –x1 = qпр
Определим х2 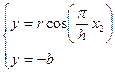 rcos(
rcos( 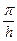 x2) = - b
x2) = - b
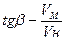 (7.1)
VМ =
(7.1)
VМ = 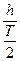 =
= 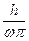 ; (7.2)
VН = r
; (7.2)
VН = r