Круговые и линейные диаграммы в трёхфазных цепях

Если меняется модуль сопротивления одной из фаз трёхфазной цепи, то геометрически местом концов векторов напряжения или тока любой из фаз будет являться окружность или прямая линия.

Для примера рассмотрим круговую диаграмму напряжения по схеме рис. 29, если Z_B = Z_C = R = const и изменяется только модуль сопротивления Z_A фазы А.

Запишем выражение для круговой диаграммы напряжения Ú_NO подобно выражению круговой диаграммы напряжения любой внутренней ветви четырёхполюсника.

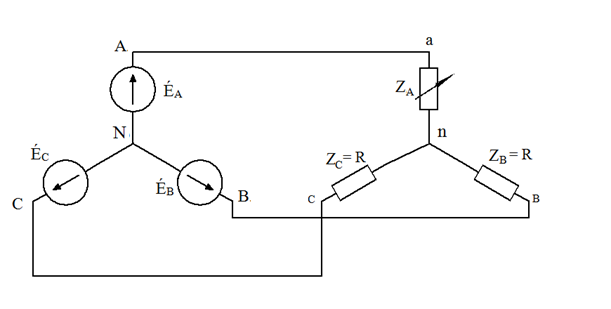
Рис. 29. Схема трёхфазной цепи

Как и раньше при построении круговых диаграмм модуль Z_А может изменяться от нуля до бесконечности, а угол ϕ_А должен быть неименным:

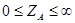ϕ_А = const

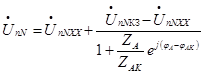(116)

В режиме холостого хода фазы А так фазы А равен нулю, а напряжение на двух сопротивлениях Z_B и Z_С равны Е́_ВС. Поскольку Z_B = Z_C = R, то точка N при холостом ходе фазы А лежит на середине вектора Е́_ВС (рис. 30).

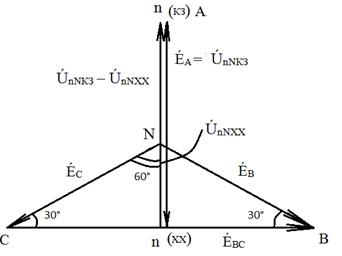
Рис. 30. Векторная диаграмма

Из рис. 30 видно, что вектор Ú_nNХХ будет направлен в противоположную сторону по отношению к Е́_А и равен его половине:

Ú_nNХХ = -0,5 Е́_А (117)

При коротком замыкании сопротивления Z_А потенциал точки О` равен потенциалу точки А, поэтому

Ú_nNКЗ = Е́_А (118)

Хордой искомой окружности является разность векторов

Ú_nNКЗ – Ú_nNХХ = Е́_А – (-0,5 Е́_А) = 1,5 Е́_А (119)

Хорда окружности направлена в ту же сторону, что и Е́_А, но она длиннее Е́_А в 1,5 раза.

Для определения входного сопротивления Z_вх= Z_Ак по отношению к точкам А и n служит схема рис. 31. Идеальные источники ЭДС закорочены, как это и положено при определении входного сопротивления.

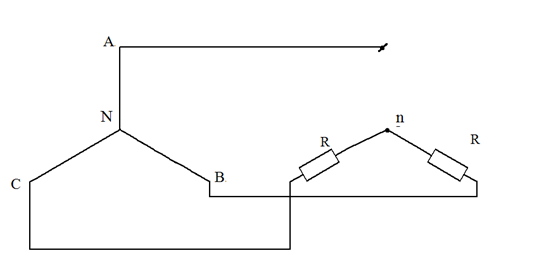
Рис. 31. Схема для определения входного сопротивления

Из схемы рис. 31 видно, что по отношению к зажимам А и n два одинаковых сопротивления R включены параллельно, поэтому

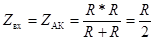(120)

Индекс К у Z_ак свидетельствует о том, что при определении входного сопротивления источники ЭДС были закорочены.

Поскольку это сопротивление активное, то его угол

ϕ_АК = 0 (121)

Рассмотрим три случая

1) Когда Z_А – изменяющееся емкостное сопротивление

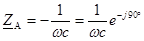, ϕ_А = -90° = const

Найдем угол ψ:

ψ = ϕ_А-ϕ_АК = -90°

Диаграмма построена на рис. 32.

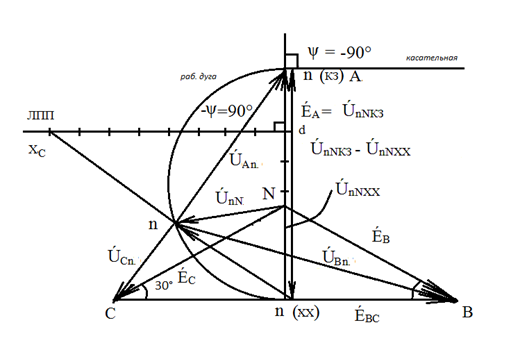
Рис. 32. Круговая диаграмма напряжения

Правила построения круговой диаграммы точно такие же, как в однофазных цепях. Напомним эти правила:

· на диаграмму наносится хорда будущей окружности. На рис. 32 она расположена между точками A и f и по длине равна 1,5Е́_А. Стрелка направлена в точку А;

· продолжаем хорду и от продолжения хорды откладываем угол ψ=-90° по часовой стрелке. Под углом ψ=-90° в точке А проводим луч, который будет являться касательной к будущей окружности;

· находим центр окружности, для чего проводим перпендикуляр к касательной и перпендикуляр к середине хорды. Перпендикуляр к касательной совпадает с хордой, т.е. хорда является диаметром окружности;

· проводим рабочую дугу окружности, помня о том, что луч, являющийся касательной, и рабочая дуга лежат по разные стороны от хорды и её продолжения;

· откладываем отрезок fd, который в масштабе сопротивления равен модулю входного сопротивления Z_АК fd*m_z =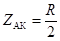

· в точке d от продолжения хорды под углом -ψ=90° проводится луч, который будет являться линией переменного параметра (ЛПП). Делается разметка этой линии в том же масштабе, что и отрезок fd.

Круговая диаграмма готова к использованию. Далее берём любой значение меняющегося сопротивления на линии переменного параметра и соединяем это с точкой f. На пересечении этой линии с рабочей дугой и будет находиться точка n для данного значения переменного параметра. Соединяем точку N и n и между ними проводим вектор искомого напряжения Ú_nN. Этот вектор содержит два слагаемых. Первое слагаемое – это Ú_nNХХ, оно неизменное. Второе слагаемое, расположенное между точками f и n - переменное, оно зависит от величины переменного параметра.

Далее точку n соединяем с точками А, В, С и получаем три вектора фазных напряжений Ú_Аn, Ú_Вn, Ú_Сn. Комплексы этих напряжений легко определить по круговой диаграмме. А зная величины сопротивлений в фазах, легко найти и линейные токи Í_A, Í_В, Í_С.

2) Когда Z_А – изменяющееся индуктивное сопротивление

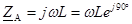, ϕ_А = 90°, ψ = ϕ_А-ϕ_АК = 90°

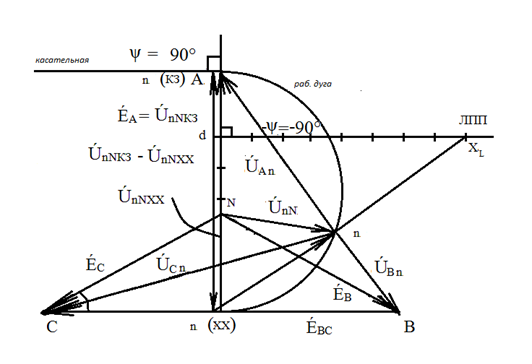
Рис. 33. Круговая диаграмма напряжения

На рис. 33 построена круговая диаграмма напряжений Ú_nN. Поскольку угол ψ = 90° положительный, то этот угол откладывают от продолжения хорды в точке А против часовой стрелки. Поэтому луч, являющийся касательной на этой диаграмме влево. Линия переменного параметра наоборот, идёт вправо. Порядок построения круговой диаграммы тот же самый.

3) Когда Z_А –изменяющееся активное сопротивление.

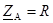, ϕ_А = 0°, ψ = ϕ_А-ϕ_АК = 0°

Продолжение хорды будет являться касательной. Поэтому перпендикуляр к касательной и перпендикуляр к середине хорды идёт параллельно, нигде не пересекаются.

Получается частный случай круговой диаграммы – линейная диаграмма.

Можно сказать, что центр окружности лежит в бесконечности, а прямая линия – это окружность бесконечно большого радиуса.

Поэтому в данном случае геометрическим местом концов вектора Ú_nN является прямая fA.