Уравнения теплообмена массива с вентиляционной струей в шахтной выработке

При проветривании возможны следующие случаи взаимодейст­вия вентиляционной струи в шахтной выработке с окружающим мас­сивом:

• стационарный режим теплообмена;

• нестационарный режим теплообмена.

Стационарный режим теплообмена имеет место в том случае, если вентиляция выработок непрерывна. При этом температура воз­душной струи и стенки выработки в заданном ее сечении остаются постоянными, но изменяются по длине выработки.

Если же проветривание подземных выработок осуществляется не постоянно или же с периодическим реверсированием вентиляци­онной струи, то имеет место нестационарный режим теплообмена. В этом случае температура воздушной струи и стенки выработки изме­няются не только по длине выработки, но и во времени в любом заданном ее сечении.

Рассмотрим в начале наиболее простой случай теплообмена -стационарный.

Коэффициент теплоотдачи от вентиляционной струи к массиву (при его охлаждении на глубоких горизонтах), или же от массива к вентиляционной струе (при проветривании выработок, пройденных в многолетнемерзлых породах) при стационарном режиме постоянен в заданном сечении выработки и меняется только по ее длине. При нестационарном он меняется и по длине выработки и во времени в любом сечении выработки.

Оценка температурного поля вокруг выработки при нестацио­нарном теплообмене будет учтена поправками к коэффициенту не­стационарного теплообмена α_τ.

Так как форма выработки на параметры теплообмена практиче­ски не влияет, то для удобства аналитического описания процесса теплообмена ее форму примем цилиндрической.

Таким образом, имеем выработку круглого сечения радиусом R_в. Температуру вентиляционной струи в заданном сечении выра­ботки обозначим через Т_в. Температура породного массива во всех его точках в начальный момент проветривания будет одинакова, обозначим ее через Т₀.

Другие обозначения примем следующие: λ — теплопроводность породы, Вт/(м -К); а — температуропроводность породы, м /с; α — коэффициент стационарного теплообмена, Вт/ (м∙К); τ — перемен­ная времени, с; r — переменная радиуса, начиная с оси выработки, м; Т — переменная температуры, К.

В принятой постановке для нахождения температурного поля вокруг цилиндрической выработки при стационарном режиме тепло­обмена необходимо решить дифференциальное уравнение теплопро­водности в цилиндрических координатах

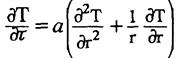(4.3)

при следующих начальных

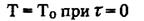(4.4)

и граничных условиях

(4.5)

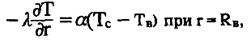(4.6)

где Т_с — температура стенки выработки, К.

Решение дифференциального уравнения (4.3) при начальных и граничных условиях (4.4)-(4.6) имеет вид:

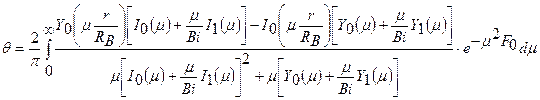(4.7)

где 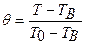- безразмерная температура для случая охлаждения массива вокруг выработки и

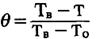— для случая его нагрева;

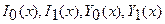— бесселевы функции первого и второго рода соответственно нулевого и первого порядка;

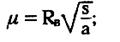
s — переменная Лапласа при замене функции f(τ) ее изображением F(s) в преобразованиях Лапласа

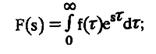
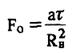— критерий Фурье;

- критерий Био.

При r = R_в безразмерная температура стенки выработки θ_с при стационарном режиме теплообмена согласно (4.7) будет равна

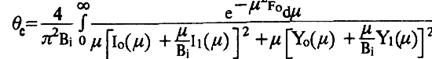(4.8)

В начальный момент 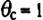, а при

При бесконечно больших значениях коэффициента теплоотда­чи а, т.е. при очень больших значениях критерия Био (Вi → ∞) урав­нение (4.7) принимает вид:

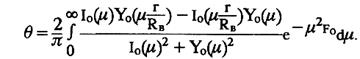
Для оценки температурного поля в массиве при нестационарном режиме теплообмена в решение (10.7) вместо критерия Био необхо­димо подставить критерий Кирпичева, который равен

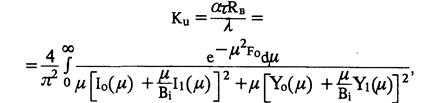(10.9)

где α_τ — коэффициент нестационарного теплообмена, Вт/(м²∙К). Пользоваться решениями для оценки θ и К_и в практических расчетах весьма затруднительно, поэтому решения (4.8) и (4.9) в виде номограмм приведены на рис. 4.1 и 4.2.

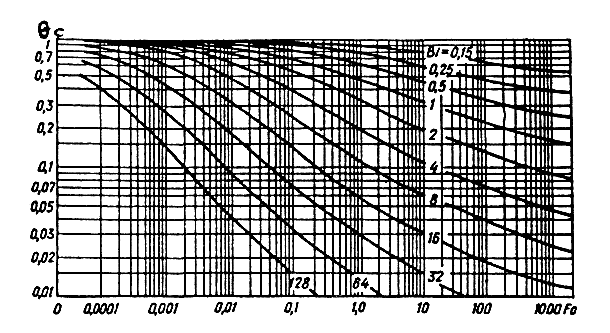
Рис. 4.1.Номограмма для определения безразмерной температуры стен шахтных выработок

Рис. 4.2. Номограмма для определения безразмерного коэффициента нестацио­нарного теплообмена (критерия Кирпичева) между горным массивом и рудничным воздухом