Элементы теории графов

Представление моделей систем в виде графов является одним из наиболее распространенных.

Граф Г – геометрическая фигура, построенная на множестве вершин V = {v₁, v₂, … v_m} и ребер R = {r₁, r₂, … r_n}:

Г = (V, R). (1)

Если ребра ориентированы, то их называют дугами, а граф - ориентированным (орграфом). При этом вершины называются узлами.

а) б)

Рис. 1

Примеры использования графов для моделирования:

1. Неориентированные графы описывают (моделируют) дороги между населенными пунктами А, B, C и D (см. рис. 1, а).

2. Орграф описывает однонаправленные каналы передачи информации (см. рис. 1, б).

Дуга r_i, связанная с злом v_j, называется инцидентной этому узлу, причем, если заходит – положительно инцидентная, если выходит – отрицательно инцидентная.

Два узла v_k и v_i смежны, если им инцидентна одна дуга. Аналогично, две дуги смежны, если они инцидентны одному узлу, причем, если одна выходит, а другая заходит – последовательно смежны, в противном случае - параллельно смежны.

Дуга, выходящая из узла и в нее же заходящая, называется петлей.

Узел, из которого дуги только выходят, называется истоком, а в который только заходят – стоком. Узлы сток и исток – висячие узлы.

Связи в системе можно изображать двояко:

1) элементы – это вершины, а связи – дуги (вершинный граф),

2) элементы – дуги, а связи – узлы (реберный или сигнальный граф).

Структуры графов можно представить как графически, так и структурными матрицами. Известны 2 вида структурных матриц: матрицы смежности, инцидентности (инциденций).

Матрица смежности – квадратная матрица А = {a_ij}, 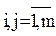, где m – число узлов, т.е. А_mxm, для которой

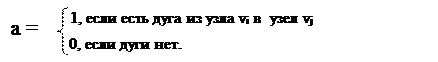
Число единиц в матрице А равно числу дуг n.

Эта матрица обладает интересным свойством: если возвести матрицу А в k-ю степень, то каждый элемент матрицы А^k будет равен числу путей из узла v_i в узел v_j длиной в k дуг.

Путь в графе – это последовательность последовательно смежных дуг, ориентированных в одном направлении.

Контур – замкнутый путь.