Классификация систем.

Системы делят на физические и абстрактные, динамические и статические, простые и сложные, естественные и искусственные, с управлением и без управления, непрерывные и дискретные, детерминированные и стохастические, открытые и замкнутые.

При делении систем на простые и сложные выделяют структурную и функциональную (вычислительную) сложность.

При оценке структурной сложности определяют число элементов, входящих в систему, и разнообразие взаимосвязей между ними.

При оценке функциональной сложности систем используют алгоритмический подход. Он основан на определении ресурсов (времени счёта и объёма памяти), используемых в системе при решении некоторого класса задач. Если время вычислений представляет собой полиноминальную функцию от входных данных, то мы имеем дело с полиномиальным по времени или «лёгким» алгоритмом. Если же время вычислений является экспоненциальной функцией от входных данных, то говорят о «сложности» алгоритма. Алгоритмическая сложность рассматривается в теории NP-полных задач.

Сложные системы делят на искусственные и естественные.

Искусственные отличаются от природных наличием определённой цели функционирования и наличием управления.

Система с управлением,имеющая входной сигнал x(t) и выходной сигнал y(t), рассматривается как преобразователь информации, перерабатывающий исходные данные x(t) в решение по управлению y(t).

В соответствии с типом значений x(t), y(t), z(t), T, системы делят на дискретные и непрерывные. Такое деление проводится с целью выбора математического аппарата описания системы. Непрерывныесистемы описываются с помощью дифференциальных уравнений. Для дискретных систем, у которых изменение состояния происходит в дискретные моменты времени, по принципу «от события к событию», описания с помощью дифференциальных уравнений не применимо. Дискретные системы описывают имитационными моделями: системы массового обслуживания: сети Петри, цепи Маркова.

Системы с входным сигналом x(t), источником которого нельзя управлять или системы, неоднозначность реакций которых нельзя объяснить разницей в состояниях, называются открытыми. Признаком открытой системы является наличие взаимодействия с внешней средой.

В области информатики открытыми информационными системами называются программно - аппаратные комплексы, обладающие следующими свойствами:

· Переносимость (мобильность). Программное обеспечение может быть легко перенесено на различные аппаратные платформы и в различные операционные среды.

· Стандартность. Программное обеспечение соответствует опубликованному стандарту независимо от конкретного разработчика.

· Наращиваемость возможностей. Включение новых программных и технических средств, не предусмотренных в первоначальном варианте.

· Совместимость. Возможность взаимодействий с другими комплексами на основе развитых интерфейсов для обмена данными с прикладными задачами в других системах.

Замкнутые (закрытые) системы - изолированные от среды системы. Не имеют ни входа, ни выхода, но и они могут интерпретироваться как генераторы информации при рассмотрении изменений их внутреннего состояния во времени. Примером замкнутой системы является локальная сеть для обработки конфиденциальной информации.

Лекция. Энтропия систем

Одной из наиболее часто используемых характеристик организации является энтропия(степень неопределенности состояния системы).

Энтропия– это количественная мера неопределённости случайного объекта или системы.

Степень организации элементов в системе связывается с изменением (снижением) энтропии системы по сравнению с суммарной энтропией элементов. Энтропия вычисляется по формуле:

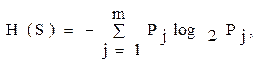(1.2)

где - вероятность j-го состояния (в теории информации – события); m - возможное число состояний (событий).

Например, два элемента А и В могут каждый принимать два равновероятных состояния: «0»и «1». Вероятность каждого состояния:

Р₁(А) = Р₂(А) = Р₁(В) = Р₂(В) = 0,5.

Для одного элемента энтропия составит

Н(А) = Н(В) = -0,5 log₂0,5 - 0,5log₂0,5 = 1.

Энтропия двух элементов:

Н(А) + Н(В) = 1 + 1 = 2. ¨

Допустим, что система S элементов А и В может принимать три состояния: «-1», «0», «1» с вероятностями Р₁(S) = Р₃(S) = 0,2; Р₂ = 0,6.

Тогда

Н(S) = -2^.0,2^.log₂0,2 - 0,6^.log₂0,6 = -0,4×(-2,32) - 0,6×(-0,737) = 1,37.

Энтропия системы S меньше суммы энтропий элементов А и В на

DН = Н(А) + Н(В) - Н(S) = 2 - 1,37 = 0,63. ¨

Для расчета изменения энтропии системы через вероятности состояний часто используется метод Колмогорова.

Допустим, дана структурная схема (граф) состояний подсистемы S (см. рис. 1.2). Исходным состоянием системы с равной степенью вероятности может быть одно из четырех состояний, т.е.

.

Будем считать, что интенсивности переходов l₂₁, l₃₂, l₄₃, l₁₄, l₂₄ заданы. Тогда можно показать, что скорости изменения вероятности нахождения системы в i-м состоянии определяются как 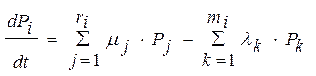, (1.3)

где 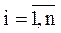; n – число узлов графа (количество состояний);

m_j 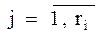- интенсивности переходов по дугам, входящим в i-й узел;

r_i – число дуг, входящих в i-й узел;

l_k 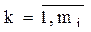- интенсивности переходов по дугам, исходящим из i-го узла;

m_i – число дуг, выходящих из i-го узла;

P_i и P_j – вероятности нахождения системы в i-м и j-м состояниях

соответственно.

Заметим, что

.

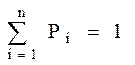Установившееся значение вероятности нахождения системы в i-м состоянии определяется из условия

.

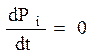Тогда для системы с n состояниями имеем систему из (n + 1) уравнений с n неизвестными:

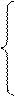
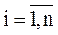; . (1.4)

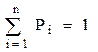
Одно из уравнений (1.4) можно отбросить, так как оно может быть получено из (n - 1) оставшихся.

Пример.Примем l₂₁ = 0,1, l₃₂ = 0,2, l₄₃ = 0,3, l₁₄ = 0,4, l₂₄ = 0,5. Тогда получаем:

l₁₄^.Р₄ - l₂₁^.Р₁ = 0

l₂₁^.Р₁ + l₂₄^.Р₄ - l₃₂^.Р₂ = 0

l₃₂^.Р₂ - l₄₃^.Р₃ = 0

l₄₃^.Р₃ – (l₁₄ + l₂₄)^.Р₄ = 0

Р₁ + Р₂ + Р₃ + Р₄ = 1.

Из системы отбросим второе уравнение и получим:

- 0,1^.Р₁ + 0^.Р₂ + 0^.Р₃ + 0,4^.Р₄ = 0

0^.Р₁ + 0,2^.Р₂ – 0,3^.Р₃ + 0^.Р₄ = 0

0^.Р₁ + 0^.Р₂ + 0,3^.Р₃ – 0,9^.Р₄ = 0

1^.Р₁ + 1^.Р₂ + 1^.Р₃ + 1^.Р₄ = 1.

Решение полученной системы: Р₁ = 0,32, Р₂ = 0,36, Р₃ = 0,24, Р₄ = 0,08.

Расчет энтропий ведется по формуле

.

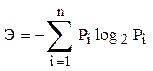Для исходного состояния

Э₀ = -4 ^. 0,25 ^. log₂0,25 = 2,

для конечного состояния

Э_к = -(0,32 ^. log₂0,32 + 0,36 ^. log₂0,36 + 0,24 ^. log₂0,24 + 0,08 ^. log₂0,08) = 1,835.

То есть, изменение энтропии составляет

DЭ = Э₀ – Э_к = 2 – 1,835 = 0,165. ¨

Таким образом, энтропия выступает в качестве меры хаоса, беспорядка и ее снижение означает увеличение организации.

Количество информации

Для информационных систем степень организации очень часто зависит от количества информации, которая может быть использована для управления.

В теории информации количество информации часто измеряют в битах (binary digital), где бит определяется как ценность I информации об исходе двух равновероятных событий. Например, эта информация о том, что сейчас день, а не ночь.

Вероятность каждого из событий

Р(Д) = 0,5; Р(Н) = 0,5;

I = log₂ 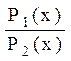, (1.5)

где Р₁(х) – апостериорная вероятность; Р₂(х) – априорная вероятность.

Для примера:

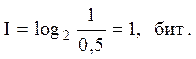
Кроме битов (термин ввел Тьюки) используются

«нат»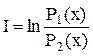

и

«дит» .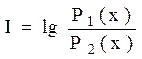

Лекция. Управление сложными системами.

Под управлением понимают процесс формирования целенаправленного поведения системы посредством информационных воздействий, формируемых человеком или устройством.

Выделяют следующие задачи управления:

· целеполагание

· стабилизация

· выполнение программы

· слежение

· оптимизация

1. Целеполагание - это определение требуемого состояния или поведения системы.

2. Стабилизация – удержание системы в существующем состоянии в условиях возмущающих воздействий.

3. Выполнение программы – перевод системы в требуемое состояние в условиях, когда значения управляемых величин изменяются по известным детерминированным законам.

4. Слежение – удержание системы на заданной траектории (обеспечение требуемого поведения системы) в условиях, когда законы изменения управляемых величин неизвестны или изменяются.

5. Оптимизация – удержание или перевод системы в состояние с экстремальным значением характеристик при заданных условиях и ограничениях.