Пример 1. Как видно (см. рис. 2), через две (k = 2) смежные дуги можно попасть: из вершины 1 в вершину 4, из 2 в 1
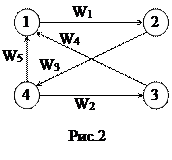
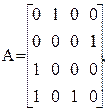
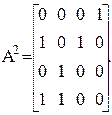
Как видно (см. рис. 2), через две (k = 2) смежные дуги можно попасть: из вершины 1 в вершину 4, из 2 в 1, из 2 в 3, из 3 в 4, из 4 в 1 и из 4 в 2. ¨
Таким образом, можно алгоритмически определить, существует ли путь из vi в vj длиной в k дуг. Очевидно, что если число узлов m, максимальная степень k, в которую нужно возвести А для определения самого длинного пути, равна (m – 1).
Матрица инцидентности – в общем случае прямоугольная матрица В = {bij}, 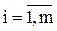 ,
, 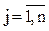 , где m – число вершин, n – число ребер. Для орграфов:
, где m – число вершин, n – число ребер. Для орграфов:
 |
Для неориентированных:
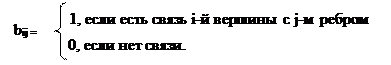 |
|



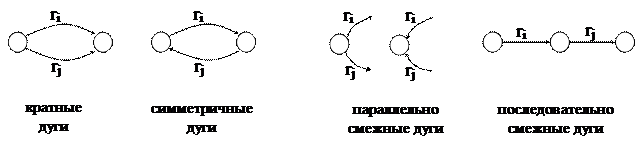
Рис. 3
Касающимися называются пути, контуры или пути с контурами, если они содержат хотя бы один общий узел.
Сильносвязанным называется граф, в котором любой узел достижим из любого другого узла.
Достижимость – это существование пути из узла vi в узел vj. Например, на рис. 3.3 путь из узла 1 в узел 4 имеет вид:
узел 1 ® W1 ® узел 2 ® W2 ® узел 3 ® W4 ® узел 4.
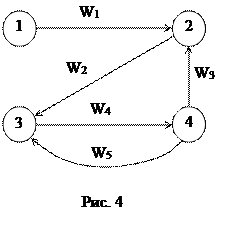 Может оказаться, что не все узлы достижимы из остальных узлов. В этом случае может быть выделен подграф Г1, т.е. совокупность, подмножество узлов, для которого условие сильной связности выполняется. Например, граф Г (см. рис. 3.4) не сильносвязный, т.к. в узел 1 из узлов 2, 3 и 4 нет путей. Сильносвязной компонентой Г1 для графа Г состоит из узлов 2, 3 и 4 с соответствующими дугами W2 – W5.
Может оказаться, что не все узлы достижимы из остальных узлов. В этом случае может быть выделен подграф Г1, т.е. совокупность, подмножество узлов, для которого условие сильной связности выполняется. Например, граф Г (см. рис. 3.4) не сильносвязный, т.к. в узел 1 из узлов 2, 3 и 4 нет путей. Сильносвязной компонентой Г1 для графа Г состоит из узлов 2, 3 и 4 с соответствующими дугами W2 – W5.
 Физический смысл сильной связности – наличие обратных связей (ОС) между всеми узлами или, другими словами, взаимозависимость (взаимовлияние) всех переменных в графе.
Физический смысл сильной связности – наличие обратных связей (ОС) между всеми узлами или, другими словами, взаимозависимость (взаимовлияние) всех переменных в графе.
Важность понятия «сильная связность» вытекает из того, что практически все целенаправленные системы строятся на основе принципа обратной связи, когда информация о выходных величинах (координатах) некоторого объекта используется для формирования управляющего сигнала U этим объектом.
Определение эквивалентных передач
Требуется установить эквивалентный оператор, описывающий связь от i-го узла к j-му узлу с учетом всех связей графа.
Для сигнальных графов Мезоном получено следующее соотношение:
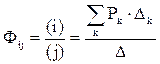 , (2)
, (2)
где Фij – передача от i-го узла к j-му узлу;
Δ – определитель графа:
 (3)
(3)
W¥,r (r = 1,2,…) - передаточный коэффициент r-го разомкнутого контура (определяется как произведение передач входящих в контур дуг),
W¥,r. W¥,p (p,r = 1, 2, …, r ¹ p) – произведение «пар» передаточных коэффициентов некасающихся контуров, далее аналогично для «троек», «четверок» и т.д. некасающихся контуров;
Pk – передача k-го прямого пути, определяемая как произведение передаточных коэффициентов дуг, образующих путь;
Δk – минор k-го прямого пути (составляется аналогично определителю, но для подграфа, полученного из исходного графа при удалении узлов, принадлежащих k-му прямому пути).
Выделение подсистем в системе
Рассмотрим формальные методы выделения подсистем, базирующиеся на двух основных подходах:
а) подсистемами считаются несвязные сильные компоненты графа. Порядок выделения следующий:
- определяется множество всех сильносвязных компонентов;
- на полученном множестве выделяется подмножество пар, троек и т.д. сильносвязных компонентов, которые являются некасающимися.
б) подсистемами считаются сильносвязные компоненты, получающиеся при удалении дуг-мостов. Анализ графа обычно проводится в предположении, что число удаляемых дуг должно быть минимально. Вначале отыскиваются единичные дуги, удаление которых нарушает сильную связность графа, но сохраняет не менее двух сильных компонент. Если таких друг нет, ищутся пары дуг, удаление которых вызывает описанный эффект и т.д.
Концептуальные методы выделения подсистем базируются на неформальных признаках выделения подсистем. Например, для графа на рис. 5,а можно насчитать пять сильносвязных компонент (кроме самого графа), но концептуально подсистемами можно считать, например, подграфы, изображенные на рис. 5, б и в.
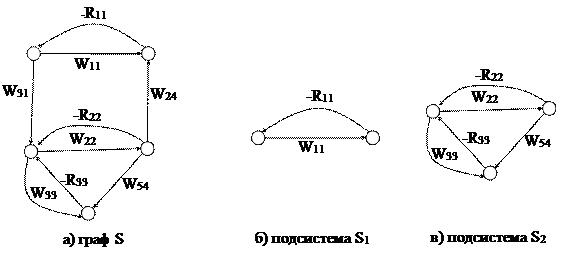

Рис. 5
Проверку силы связности компонент можно осуществлять различными методами, в частности методом Вавилова-Имаева.
Рассмотрим этот метод на примере графа, изображенного на рис. 6. Предположим, что системы S1 и S2 не связаны, то есть организованы в систему S ошибочно. Определитель такой несвязной системы будет равен
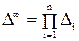 , (4)
, (4)
где n – число подсистем (в примере n = 2), Δi – определитель i-й подсистемы.
В примере
Δ1 = 1 + W11.R11, Δ2 = 1 + W22.R22, (5)
Δ¥ = 1 + W11.R11 + W22.R22 + W11.R11.W22.R22. (6)
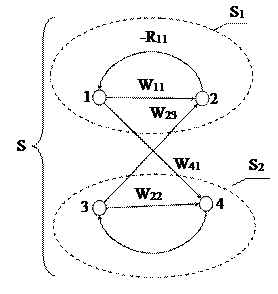 |
Рис. 6
Определитель системы с учетом существующих связей:
Δ = 1 + W11.R11 + W22.R22 + W11.R11.W22.R22 – W23.R11.W41.R22. (7)
Можно видеть, что разность определителей
δΔ = Δ - Δ¥ = – W23.R11.W41.R22. (8)
Очевидно, что если
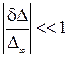 , (9)
, (9)
«добавкой» δΔ можно пренебречь и подсистемы S1 и S2 рассматривать как независимые. Модуль в (4.12) берется потому, что, во-первых, «добавка» δΔ может быть как со знаком «+», так и со знаком «-», во-вторых, значения δΔ, Δ и Δ¥ - это не обязательно действительные числа. Операторы передач Wij, Kkp (i, j, k, p – целые числа) могут быть произвольными объектами, в том числе комплексными числами и матрицами. Поэтому модуль может пониматься, по крайней мере, в трех смыслах:
- для действительных чисел – число без знака (со знаком «+»);
- для комплексных чисел p = α + j.ω, где  - мнимая единица:
- мнимая единица:
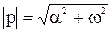 ; (10)
; (10)
- для матриц – определитель матрицы.
Метод логического ранжирования
Метод используется для задач составления расписаний.
Назначение метода: упорядочивание этапов выполнения некоторых работ.
Предположим, что имеется набор работ (этапов выполнения работ), причем некоторые виды работ не могут быть начаты до того, как будут окончены другие работы. Например, определены причинно-следственные отношения между отдельными работами (см. рис. 7): работа Р0 является завершающей, ей должны предшествовать работы Р1, Р2 и Р3, работе Р1 должны предшествовать работы Р4, Р5 и Р9 и т.д. Продолжительность каждой работы примем за единицу.
Для принятия решений нужно выработать критерий, по которому будет происходить оптимизация. В качестве критерия возьмем вес работы. Он тем больше, чем раньше работу необходимо выполнить. Для решения задачи составляется матрица весов (см. табл. 1).
В последней колонке таблицы отмечены веса каждой работы, равные сумме чисел в соответствующей строке. Отсюда можно определить последовательность выполнения работ:
Р11, Р14 ® Р12, Р13 ® Р7, Р10 ® Р5, Р6, Р8 ® Р4, Р9 ® Р1, Р2, Р3.
То есть, сначала выполняются работы Р11 и Р14, после них Р12 и Р13 и т.д. Может быть учтена неравнозначность видов работ, выполняющихся одновременно.
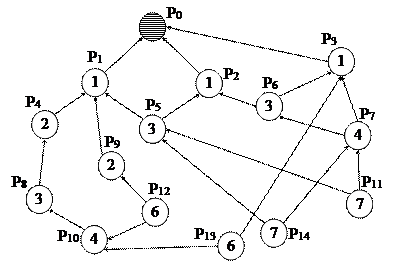
Рис. 7
Таблица 1
| Р0 | Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | Р7 | Р8 | Р9 | Р10 | Р11 | Р12 | Р13 | Р14 | Σ | |
| Р0 | ||||||||||||||||
| Р1 | ||||||||||||||||
| Р2 | ||||||||||||||||
| Р3 | ||||||||||||||||
| Р4 | ||||||||||||||||
| Р5 | ||||||||||||||||
| Р6 | ||||||||||||||||
| Р7 | ||||||||||||||||
| Р8 | ||||||||||||||||
| Р9 | ||||||||||||||||
| Р10 | ||||||||||||||||
| Р11 | ||||||||||||||||
| Р12 | ||||||||||||||||
| Р13 | ||||||||||||||||
| Р14 |
Метод анализа иерархий
Это один из достаточно формализованных и классических методов СА, используемый для разрешения проблемы принятия решений в условиях многокритериальности.
Назначение и идея метода: проводится иерархическая декомпозиция проблемы на задачи таким образом, чтобы облегчить человеку принятие решений для отдельных задач на основе парных, а не многокритериальных сравнений. После этого синтез приоритетов проводится математическими методами.
Название метода связано с тем, что сначала для проблемы строится иерархия задач, а затем эти задачи решаются, начиная с нижнего уровня, при этом результат решения задач нижнего уровня используется при решении задач более высоких уровней.
Дата добавления: 2015-07-30; просмотров: 935;
