Схема перевозок стали
| в Q1 | в Q2 | в Q3 | … | в Qk | Отправлено | |
| из P1 | x11 | x12 | x13 | … | x1k | a1 |
| из Р2 | x21 | x22 | x23 | … | x2k | a2 |
| … | … | … | … | … | … | … |
| из Pm | xm1 | xm2 | xm3 | … | xmk | am |
| Привезено | b1 | b2 | b3 | … | bk |
Первое условие примет вид
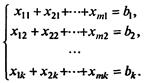 (7.74)
(7.74)
Второе условие примет вид
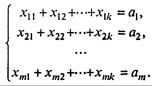 (7.75)
(7.75)
Раз стоимость перевозки одной тонны из Рi в Qj равна cij, то общая стоимость S всех перевозок равна
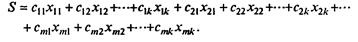 (7.76)
(7.76)
Таким образом, мы приходим к следующей чисто математической задаче: дана система m+k линейных алгебраических уравнений (7.74) и (7.75) c m∙k неизвестными (обычно т∙k >> m+k) и линейная функция S. Требуется среди всех неотрицательных решений данной системы найти такое, при котором функция S достигает наименьшего значения (минимизируется).
Практическое значение этой задачи огромно, ее умелое решение в масштабах нашей страны могло бы экономить ежегодно огромные средства.
Пример 3. Задача о диете. Пусть у врача-диетолога имеется n различных продуктов F1, F2, ..., Fn, из которых надо составить диету с учетом их питательности. Пусть для нормального питания человеку необходимо т веществ N1, N2, ..., Nm. Предположим, что за месяц каждому человеку необходимо γ1 кг вещества N1, γ2 кг вещества N2, ..., γm кг вещества Nm. Для составления диеты необходимо знать содержание питательных веществ в каждом продукте. Обозначим через αij количество i-го питательного вещества, содержащегося в одном килограмме j-го продукта. Всю эту информацию представляют в виде, так называемой, матрицы питательности (табл. 7.11).
Таблица 7.11
Дата добавления: 2015-07-30; просмотров: 577;
