РЕКУРСИВНЫЕ АЛГОРИТМЫ

Изучая в предыдыщем разделе язык Паскаль, мы уже использовали понятие рекурсии. Однако, оно столь важно и принципиально, что с ним следует познакомиться детальнее.

Рекурсией называют метод определения или вычисления функции, процедуры или решения задачи посредством тон же функции, процедуры и т.д. Рекурсивные алгоритмы широко используют методы частных целей, подъема и отрабатывания назад. На эвристическом уровне рекурсия позволяет эффективно использовать метод проб и ошибок.

Продолжим рассмотрение примера задачи тура шахматного коня из предыдущего раздела. Приведенный там алгоритм строил возможный путь коня по простой стратегии очередного хода на свободное место по принципу часовой стрелки. Однако, он не позволял гарантированно найти полный тур коня. Применим простую эвристическую модель решения задачи - в случае отсутствия возможности очередного хода осуществляется возврат коня на предыдущее поле и возобновление поиска дальнейшего маршрута по другому пути. Подобный процесс называют возвратом (или откатом). Его можно осуществлять по универсальной схеме:

procedureRETR;

begin

инициализация начального хода repeat выбор очередного хода

if подходит then его запись;

if решение не полное then RETR;

if неудача then стирание хода и возвратна предыдущий until удача or нет хода

end.

Подобная рекурсивная процедура и уже известный алгоритм, рассмотренный выше, позволяют построить нужную программу. Ниже представлена программа тура коня для произвольного поля NxN, позоляющая отыскивать полный тур с любого начального положения. Для наглядной иллюстрации процесса поиска в глубину и в ширину с возвратами в программе в комментарные скобки обозначены команды вывода промежуточных результатов.

Программа 39

program tur;

var i, j, ii, jj, n, nn: integer; q: boolean;

dx, dy:array[1..8] of integer; h:array[1..8,1..8] of integer;

(*рекурсивная процедура - попытка сделать ход*)

procedure try(i,x,у:integer; var q:boolean);

var k, u, v: integer; ql: boolean;

begin

k:=0; repeat k:=k+l; ql:=false; u:=x+dx[k]; v:=y+dy(k];

if ( (1<=u) and(u<=n) and (1<=v) and (v<=n) ) and(h[u,v]=0)

then begin h[u,v]:=i;

(*для отладки и наблюдения процесса поиска с возвратом*')

for ii:=l to n do begin for jj:= 1 to n do

write(h[ii,jj]:5); writeln;

end;

readin;

if i<nn then begin try(i+l,u,v,ql);

if not(ql) then h[u,v]:=0

else ql:=truer;

end

else ql:=true

end;

until (ql) or (k=8);

q:=ql

end; (* конец процедуры*)

begin

dx[l] =2: dx[2]:=l; dx[3]:=-l; dx[4]:=-2; dx[5]:=-2;

dx[6] =-1: dx[7]:=l; dx[8]:=2; dy[l]:=l; dy[2]:=2;

dy[3] =2: dy[4]:=l; dy[5]:=-l; dy[6]:=-2;

dy[7] =-2: dy[8]:=-1;

write ('введи n: '); readln(n);

for i =1 to n do for j:=1 to n do h[i,j]:=0;

write; ('введи i,j : '); readln(i,j); nn:=n*n;

h[i,j]:=l; try(2,i,j,q);

if q then begin

for i:=l to n do begin

for j:= 1 to n do write(h[i,j]:5);

writeln;

end;

end ' else writeln( 'нет маршрута');

readln

end.

Для n = 5 и n = 6 алгоритм быстро находит искомые туры коня. Для n = 8 время решения может возрасти в несколько десятков раз.

Рассмотрим еще два замечательных рекурсивных алгоритма, позволяющих строить регулярные образы, в конечном счете образующие красивые узоры на экране дисплея. Узор образуется из серии выстраиваемого определенным образом заданного мотива. '

Ниже представлена программа, использующая при построении узора кривые Серпинского, рис. 3.13.

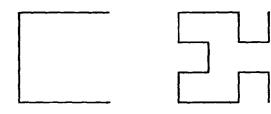
Рис. 3.13. Примеры кривых Серпинского

На рисунке изображены кривые Серпинского S1 и S2 первого и второго порядков. Кривую Серпинского Si можно разбить на 4 части: Ai, Bi, Ci, Di, которые соединяются четырьмя отрезками Эти четыре части кривой представляют одну и ту же ломаную, поворачивающуюся каждый раз на 90 градусов. Нетрудно увидеть рекурсивные схемы, по которым ломаные Ai, Bi. Ci, Di получаются из кривых A(i-l). B(i-l), C(i-l), D(i-l), размеры которых при этом сокращаются вдвое:

Векторы, соединяющие отдельные элементы кривых, образуют с осью абсцисс углы, кратные pi/4; средние векторы во всех схемах имеют длину, в два раза большую, чем крайние. Для построения вектора длины U под углом T*pi/4 к оси абсцисс в программе описана процедура linep(T,U:integer):

Программа 40

program serpinsk;

uses crt,graph;

const sq=512;

var i, xO, yO, x, y, t, u, gd, gm: integer; ch:chart;

procedure linep(t,u:integer);

var xl, yl:integer;

begin x:=x+round(u*cos(t*pi/4)) ;

y:=y-round(u*sin(t*pi/4)); lineto(x,y) ;

end;

procedure b(i:integer); forward;

procedure с(i:integer); forward;

procedure d(i:integer); forward;

procedure a(i:integer);

begin

if i>0 then begin a(i-l); linep(7,u); b(i-l); linep(0,2*u);

d(i-l); linep(l,u); a(i-l)

end end; •

procedure b;

begin

if i>0 then begin b(i-l); linep(5,u); c(i-l); linep(6,2*u);

a(i-l); linep(7,u); b(i-l)

end end;

procedure c;

begin

if i>0 then begin c(i-l); linep(3,u); d(i-l); linep(4,2*u) ;

b(i-l); linep(5,u);C(i-l)

end end;

procedure d;

begin

if i>0 then begin d(i-l); linep(l,u); a(i-l); linep(2,2*u);

c(i-l); linep(3,u); d(i-l) end. end;

begin gd:=0; initgraph(gd, gm, ' ' );

u:=sq div 4; x0:=320; y0:=128; i:=0;

repeat

i:=i+l; x0:=x0-u; u:=u div 2; y0:=y0-u;

x:=x0; y:=y0; setcolor(2*i);

moveto(x,y); a(i); linep(7,u); b(i);

linep(5,u); c(i); linep(3,u);

d(i); linep(l,u); delay(2000) until i=5;

settextstyle(0,0,1) ;

outtextxy(200, 470, 'КРИВЫЕ СЕРПИНСКОГО S1 - S5');

readln; closegraph

end.

В 1891 г. Д. Гильберт открыл серию рекурсивных кривых, которые получили название кривых Гильберта. Кривая Гильберта Hi, подобно кривым Серпинского, может быть получена из четырех экземпляров кривой H(i-l) вдвое меньшего размера, повернутых должным образом и соединенных отрезками. Ниже приводится программа, рисующая узор из шести кривых Гильберта.

Программа 41

program hilbert;

uses crt,graph;

const sq=448;

var i,x0,y0,x,y,t,u,gd,gm:integer; ch:char;

procedure linep(t,u:integer);

var xl,yl:integer;

begin x:=x+round(u*cos(t*pi/4)); y:=y-round(u*sin(t*pi/4)) ;

lineto (x,y) ;

end;

procedure b(i:integer); forward;

procedure с(i:integer); forward;

procedure d(i:integer); forward;

procedure a(i:integer);

begin

if i>0 then begin d(i-l); linep(4,u); a(i-l); linep(6,u);

a(i-l); linep(0,u); b(i-l)

end end;

procedure b;

begin

if i>0 then begin c(i-l); linep(2,u); b(i-l); linep(0,u);

b(i-l); linep(6,u); a(i-l)

end end;

procedure c;

begin

if i>0 then begin b(i-l); linep(0,u); c(i-l); linep(2,u);

c(i-l); linep(4,u); d(i-l)

end end;

procedure d;

begin

if i>0 then begin a(i-l); linep(6,u); d(i-l); linep(4,u);

d(i-l); linep(2,u); c(i-l)

end end;

begin gd:=0; initgraph(gd, gm, ' '); x0:=320; y0:=240; u:=sq; i:=0;

repeat

i:=i+l; u:=u div 2;

x0:=x0+(u div 2); y0:=y0-(u div 2) ;

x:=x0; y:=y0; setcolor(2*i);

moveto(x,y); a(i); delay(2000) until i=6;

settextstyle(0,0,1) ;

outtextxy(220,470, 'КРИВЫЕ ГИЛЬБЕРТА HI - Н6');

readin; closegraph

end.