Метод суперпозиции
Рассмотрим метод суперпозиции (наложения) на схеме рис. 26.
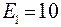
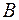
 ;
;
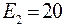 В;
В;
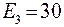 В;
В;
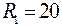 Ом;
Ом;
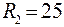 Ом;
Ом;
 Ом.
Ом.
|
Суть метода в том, что каждый истинный ток равен алгебраической сумме токов частных режимов, рассчитанных от каждого из источников поочерёдно. То есть у каждого тока столько слагаемых, сколько в схеме источников.
Так, в схеме рис. 26 три источника 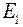 ,
, 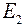 ,
, 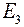 . Поэтому у каждого из токов
. Поэтому у каждого из токов 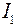 ,
, 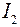 ,
, 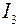 будет три слагаемых.
будет три слагаемых.
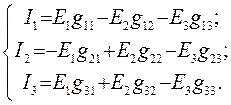 (78)
(78)
Здесь 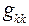 − входные проводимости схемы относительно разрыва в k-ой ветви;
− входные проводимости схемы относительно разрыва в k-ой ветви;
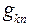 − взаимные проводимости схемы между k-ой и n-ой ветвями.
− взаимные проводимости схемы между k-ой и n-ой ветвями.
На рис. 27 изображена схема первого частного режима, когда оставлена ЭДС 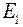 , а источники
, а источники 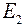 и
и 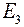 закорачиваются, если они идеальные. Если источники реальные, то на их месте включаются их внутренние сопротивления.
закорачиваются, если они идеальные. Если источники реальные, то на их месте включаются их внутренние сопротивления.
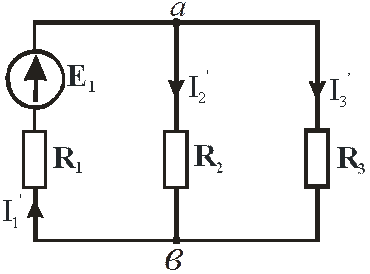
Рис. 27
Первый столбец в уравнении (78) и соответствует первому частному режиму рис. 27. По схеме рис. 27 можно найти входную проводимость схемы относительно разрыва в первой ветви 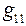 , и взаимную проводимость между второй и первой ветвями
, и взаимную проводимость между второй и первой ветвями 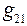 и взаимную проводимость между третьей и первой ветвями
и взаимную проводимость между третьей и первой ветвями 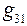 .
.
Сначала найдём ток входной верви 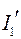 :
:
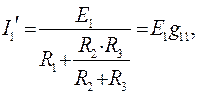 (79)
(79)
отсюда
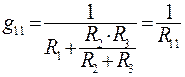 , (80)
, (80)
где 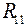 − входное сопротивление схемы относительно разрыва в первой ветви.
− входное сопротивление схемы относительно разрыва в первой ветви.
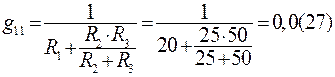
 .
.
Далее найдём токи 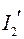 и
и 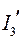 :
:
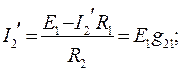 (81)
(81)
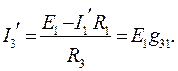 (82)
(82)
отсюда
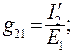 (83)
(83)
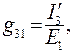 (84)
(84)
и в общем случае
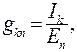 (85)
(85)
т.е. взаимная проводимость между k-ой и n-ой ветвями равна току 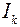 в k-ой ветви, делённому на ЭДС
в k-ой ветви, делённому на ЭДС 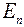 , включенной в n-ой ветви.
, включенной в n-ой ветви.
Если в выражениях (79), (83), (84) взять 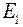 равной одному вольту, то входная проводимость
равной одному вольту, то входная проводимость 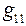 будет численно равна току первой ветви от ЭДС один вольт, включённой в ту же первую ветвь, а взаимные проводимости
будет численно равна току первой ветви от ЭДС один вольт, включённой в ту же первую ветвь, а взаимные проводимости 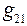 и
и 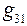 будут численно равны соответственно токам второй и третьей ветвей от ЭДС один вольт, включенной в первую ветвь. Поэтому простейший способ нахождения входных и взаимных проводимостей − это в схеме частного режима найти токи во всех ветвях от ЭДС один вольт.
будут численно равны соответственно токам второй и третьей ветвей от ЭДС один вольт, включенной в первую ветвь. Поэтому простейший способ нахождения входных и взаимных проводимостей − это в схеме частного режима найти токи во всех ветвях от ЭДС один вольт.
Так, в выражении (80) единицу в числителе можно считать за ЭДС один вольт.
Тогда
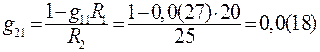
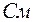 ; (86)
; (86)

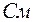 . (87)
. (87)
На рис. 28 изображена схема второго частного режима, когда оставлена ЭДС 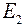 , а источники
, а источники 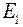 и
и 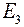 закорочены, поскольку считаем их идеальными.
закорочены, поскольку считаем их идеальными.
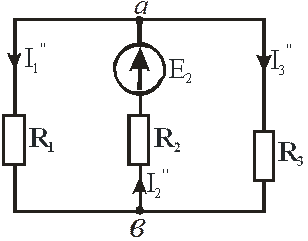
Рис. 28
Найдём входную проводимость 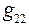 и взаимные проводимости
и взаимные проводимости 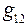 , и
, и 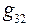 , считая, что ЭДС Е2 равна одному вольту:
, считая, что ЭДС Е2 равна одному вольту:
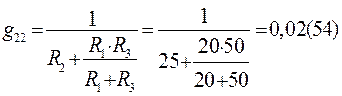
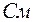 ; (88)
; (88)
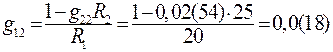
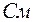 ; (89)
; (89)
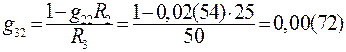
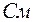 . (90)
. (90)
На схеме рис. 29 изображена схема третьего частного режима, когда оставлена ЭДС Е3, а источники Е1 и Е2 закорочены, поскольку считаем их идеальными.
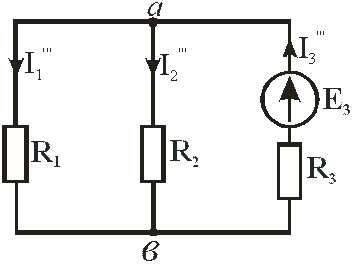
Рис. 29
Найдём входную 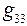 и взаимные
и взаимные 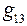 и
и 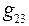 проводимости, считая, что ЭДС
проводимости, считая, что ЭДС 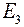 равна одному вольту:
равна одному вольту:
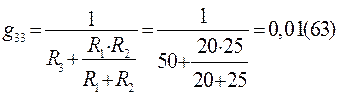
 ; (91)
; (91)
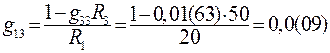
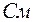 ; (92)
; (92)
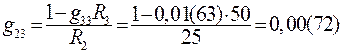
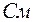 . (93)
. (93)
Очевидно, что 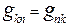 , поэтому
, поэтому
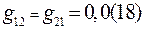
 ;
; 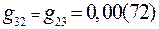
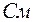 ;
; 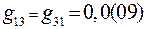
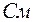 , хотя они и рассчитаны по разным схемам частных режимов.
, хотя они и рассчитаны по разным схемам частных режимов.
Все входные и взаимные проводимости найдены. Теперь найдём токи в схеме рис. 26. Правило знаков в формулах (78) следующие: произведение ЭДС на проводимость берётся со знаком плюс, если направление тока частного режима совпадает с направлением тока в исходной схеме, и минус− если не совпадает.
Так, в схеме рис. 27 направления токов частного режима 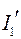 и
и 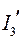 совпадает с направлениями токов
совпадает с направлениями токов 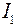 и
и 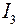 в исходной схеме, поэтому
в исходной схеме, поэтому 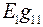 и
и 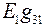 взяты со знаком плюс. А направление тока
взяты со знаком плюс. А направление тока 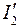 частного режима противоположно направлению тока
частного режима противоположно направлению тока 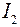 в исходной схеме. Поэтому
в исходной схеме. Поэтому 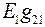 взято со знаком минус. Те же правила и для других частных режимов.
взято со знаком минус. Те же правила и для других частных режимов.
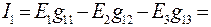
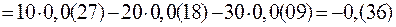
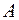 ;
;
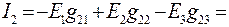
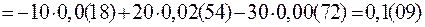
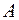 ;
;
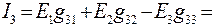
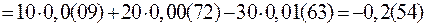
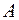 .
.
Проверим правильность расчёта с помощью баланса мощностей.
Сначала найдём мощность источников:
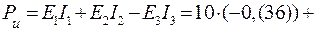
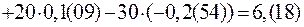
 . (94)
. (94)
Последнее слагаемое в выражении (94) взято со знаком минус, потому что направления ЭДС 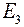 и тока
и тока 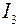 противоположны.
противоположны.
Мощность приёмников:
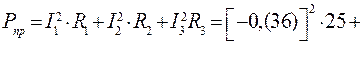

 . (95)
. (95)
Как видно из расчёта, мощность источников энергии 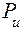 равна мощности приёмников
равна мощности приёмников 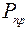 , т.е. баланс мощностей выполняется и значит токи рассчитаны верно.
, т.е. баланс мощностей выполняется и значит токи рассчитаны верно.
Если все ЭДС 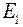 ,
, 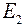 ,
, 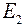 в схеме рис. 26 заданы и не меняются, т.е. требуется рассчитать схему только в одном режиме, то быстрее можно рассчитать токи, алгебраически сложив токи трёх частных режимов:
в схеме рис. 26 заданы и не меняются, т.е. требуется рассчитать схему только в одном режиме, то быстрее можно рассчитать токи, алгебраически сложив токи трёх частных режимов:
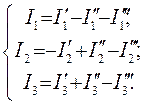 (96)
(96)
Если же требуется исследовать работу схемы рис. 26 в различных режимах, в которых ЭДС 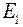 ,
, 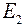 ,
, 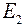 изменяется и по величине и по направлению, то необходимо пользоваться формулами (78) с использованием входных и взаимных проводимостей.
изменяется и по величине и по направлению, то необходимо пользоваться формулами (78) с использованием входных и взаимных проводимостей.
Всё дело в том, что входные и взаимные проводимости не зависят от величины и направления ЭДС в ветвях схемы, а зависят только от схемы соединения и величины резисторов. Поэтому один раз, определив все входные и взаимные проводимости, можно быстро рассчитать токи в любых режимах при любой величине и направлении ЭДС 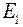 ,
, 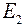 ,
, 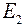 , записывая каждый раз для отдельного режима выражения, подобные выражениям (78), а также правильно учитывая знаки.
, записывая каждый раз для отдельного режима выражения, подобные выражениям (78), а также правильно учитывая знаки.
Дата добавления: 2015-07-30; просмотров: 1165;
