Метод контурных токов. Как показал Максвелл ещё в 1873г., число уравнений для расчёта токов и напряжений в электрической цепи может быть уменьшено
Как показал Максвелл ещё в 1873г., число уравнений для расчёта токов и напряжений в электрической цепи может быть уменьшено, если составлять их по одному из законов Кирхгофа, т.е. только для контуров или только для узлов.
Ток в любой ветви электрической цепи всегда можно представить составленным из нескольких токов, каждый из которых замыкается но своему контуру, оставаясь вдоль него неизменным. Такие составляющие действительных токов называют контурными. Ток в любой ветви, принадлежащей только одному контуру, совпадает с контурным. Ток в ветви, принадлежащей сразу двум или нескольким контурам, равен алгебраической сумме соответствующих контурных токов. Контурные токи, проходя через узел, остаются непрерывными, следовательно, первый закон Кирхгофа выполняется автоматически. Поэтому уравнения с контурными токами составляются только по второму закону Кирхгофа. Число таких независимых уравнений равно числу независимых контуров:
К2=В-(У-1)
В заданной схеме К2=7-(5-1)=3, т.е. необходимо составить три уравнения для независимых контуров, например admва,aвса, aсndа.
Выберем произвольно направления контурных токов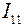 
, 
, 
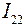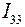, например, как на рис. 10. Система контурных уравнений в наиболее общем случае, т.е. когда в схеме имеются и источники ЭДС и источники тока, имеет следующий вид [1]:
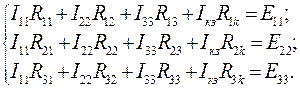(37)
Здесь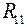 
, 
, 
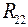- суммарное сопротивление соответственно первого, второго и третьего контуров;
, 
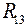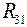- сопротивление, общее для первого и третьего контуров;
, 
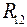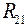- сопротивление, общее для первого и второго контуров;
, 
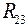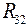- сопротивление, общее для второго и третьего контуров;
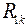- сопротивление первого контура, по которому протекает ток от источника тока;
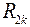- сопротивление второго контура, но которому протекает ток от источника тока;
- сопротивление третьего контура, но которому протекает ток от источника тока;
, 
, 
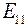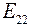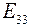- сумма ЭДС соответственно первого, второго и третьего контуров. Очевидно, что
; 
; 
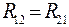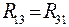. (38)
При составлении контурных уравнений следует руководствоваться следующими правилами:
1. Если ЭДС совпадает с направлением контурного тока, то она берёгся со знаком плюс, если не совпадает - со знаком минус.
2. Знак сопротивления, общего для двух контуров (а
следовательно, и падения напряжения на этом резисторе),
берётся отрицательным, если направления контурных токов противоположны; если они совпадают, то - положительным.
3. Знак сопротивления, какого- либо контура, по которому замыкается ток Ikз от источника тока, будет положительным, если направление контурного тока совпадает с направлением тока Ikз от источника тока; если эти токи противоположны, то берётся знак минус.
Для схемы рис. 10 входные и взаимные сопротивления:
;
;
;
;
;
;
; 
; 
.
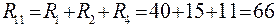
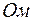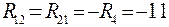
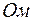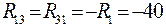
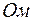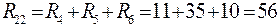
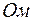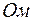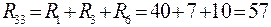
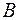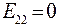
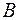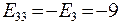
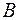Так как условились, что ток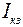 
проходит только по резистору 
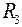, то
; 
; 
.
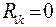
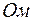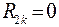
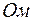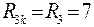
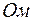Подставив эти величины в систему уравнений (37) получим следующую систему уравнений:
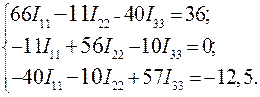(39)
Найдём определители этой системы:
;
;
;
.
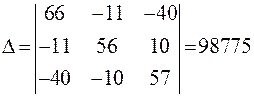
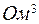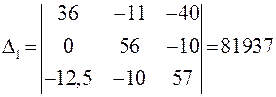
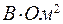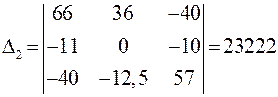
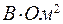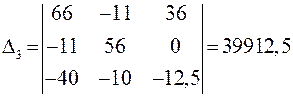
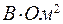Вычислим контурные токи:
;
;
.
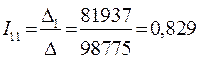
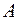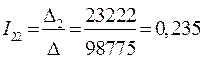
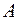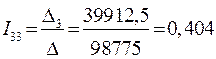
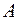Определим далее токи в ветвях по контурным токам. Ток в ветви, принадлежащей только одному контуру, равен контурному току и берётся со знаком "плюс", если он совпадает с направлением контурного тока; если не совпадает, то - со знаком "минус".
Ток в ветви, принадлежащей двум или нескольким контурам, равен алгебраической сумме соответствующих контурных токов. Со знаком плюс берутся контурные токи, совпадающие с током этой ветви, со знаком "минус"- не совпадающие с ним.
Для схемы рис.10 результат расчета имеет вид
;
;
;
;
;
;
.
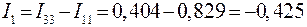
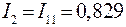
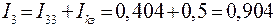
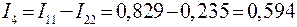
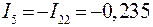
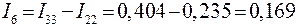
Чтобы убедиться в правильности полученных результатов, необходимо контурные токи подставить в уравнения (39):
;
;
.
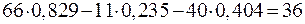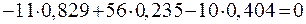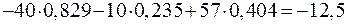Проверка показывает, что полученные результаты правильные.
Дата добавления: 2015-07-30; просмотров: 541;