Потенциальная диаграмма
Потенциальная диаграмма строится для правильного понимания того, как изменяется потенциал вдоль выбранного контура электрической цепи. На оси ординат откладываются значения потенциала, а на оси абсцисс - точки выбранного контура, причем расстояние между точками целесообразно брать пропорциональными сопротивлению ветви, соединяющей соседние точки.
Построим потенциальную диаграмму контура авmdnса на схеме рис. 10, содержащего две ЭДС.
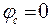
 ;
; 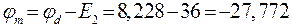
 ;
;
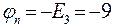
 ;
; 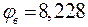
 ;
; 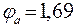
 ;
;

 ;
; 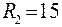
 ;
; 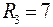
 ;
;
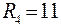
 ;
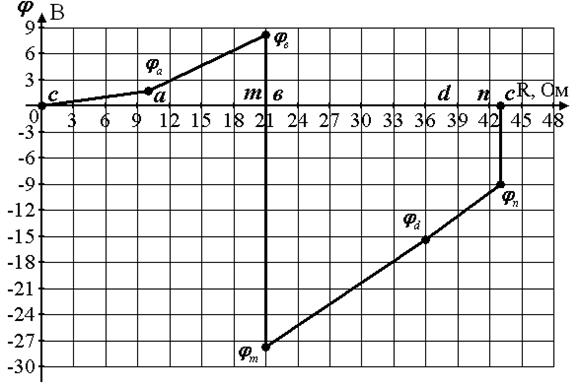
; 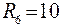
 .
.
Потенциальная диаграмма для указанного контура показана на рис. 17.
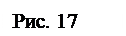
12. Пример выполнения расчётно-графической работы "Линейные цепи постоянного тока"
Рассчитать разветвленную цепь постоянного тока по схеме
рис. 18.
В данной схеме число ветвей В=7, число узлов У=5. Выберем произвольно направление токов в ветвях так, как показано на рис. 18.
Выберем на схеме независимые контуры и направления обхода в них согласно рис. 18.
1. Составим уравнения по первому и второму закону Кирхгофа:
К1=У-1=5-1=4. (52)
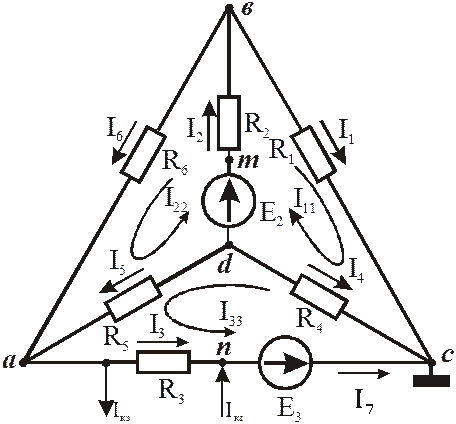
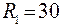
 ;
;
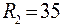
 ;
;
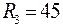
 ;
;
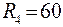
 ;
;
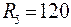
 ;
;
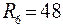
 ;
;
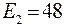
 ;
;
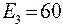
 ;
;
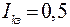
 .
.
Рис. 18
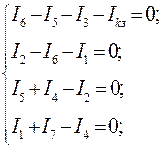
(а)
 | |||
| |||
К2=В-(У-1)=7-4=3; (54)
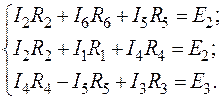 (55)
(55)
2. Определим токи во всех ветвях методом контурных токов. Направим контурные токи так, как показано на рис. 18.
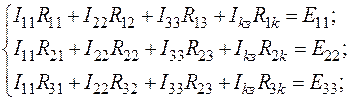 (56)
(56)

 ;
;
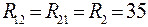
 ;
;
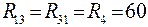
 ;
;
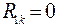
 ;
; 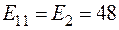
 ;
;
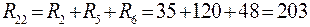
 ;
;

 ;
;
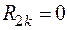
 ;
; 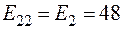
 ;
;
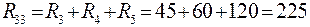
 ;
;
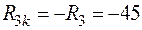
 ;
; 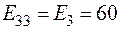
 ;
;
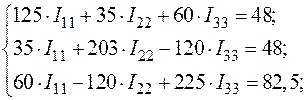 (57)
(57)
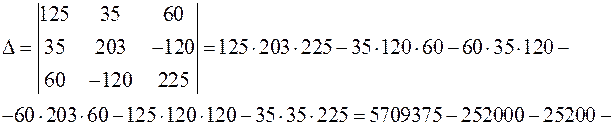
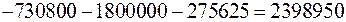
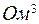 ;
;
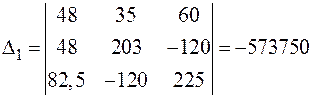
 ;
;

 ;
;

 ;
;
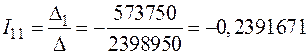
 ;
;
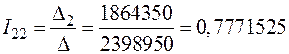
 ;
;
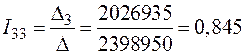
 ;
;

 ;
;
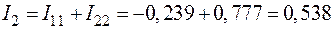
 ;
;
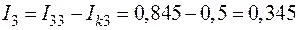
 ;
;
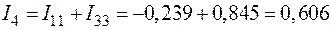
 ;
;
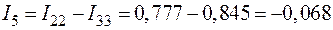
 ;
;
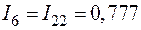
 ;
; 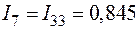
 .
.
Для проверки подставим полученные значения токов в уравнения (53) и (55), составленные по первому и второму законам Кирхгофа.
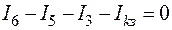 ;
;
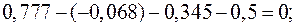
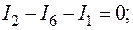
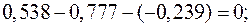
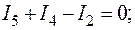
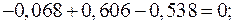
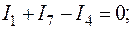
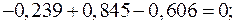
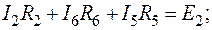
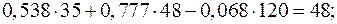
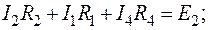
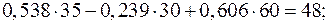
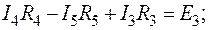
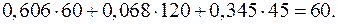
Тождества выполняются, значит токи найдены верно.
Покажем на этом примере, что тот же результат получится, если в схеме рис. 18 источник тока заменить на источник ЭДС 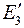 , причём
, причём
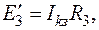 (58)
(58)
а направление действия ЭДС Е3’ встречно направлению тока 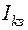 .
. 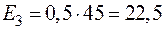
 .
.
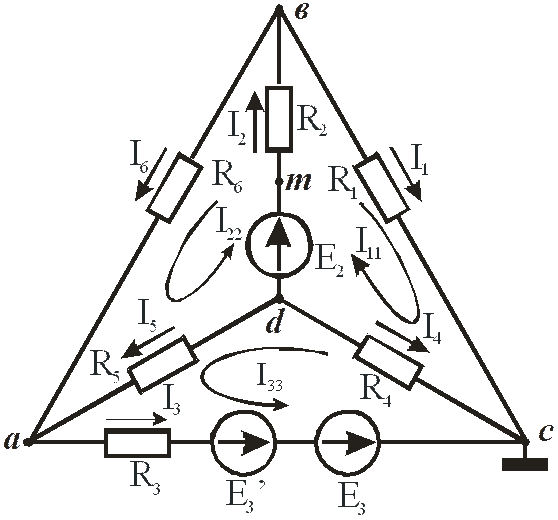
Рис. 19
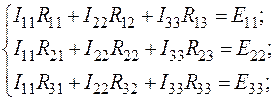 (59)
(59)

 ;
;
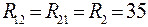
 ;
; 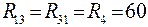
 ;
;
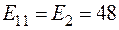
 ;
;
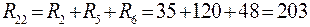
 ;
;

 ;
;
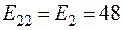
 ;
;
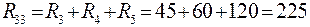
 ;
;
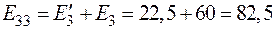
 ;
;
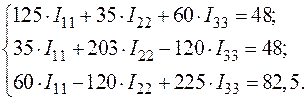 (60)
(60)
Система уравнений (60) имеет точно такой же вид, как и система (57).
Решение системы:
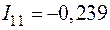
 ;
; 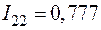
 ;
; 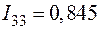
 ;
;

 ;
;
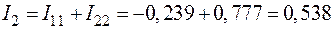
 ;
;
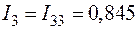
 ;
;
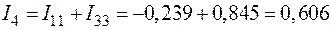
 ;
;
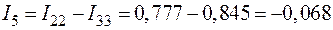
 ;
;
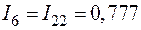
 .
.
3. Определим токи во всех ветвях методом узловых потенциалов.
Для схемы рис. 18
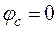
 , а значит
, а значит 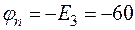
 . (61)
. (61)
Составим узловые уравнения для оставшихся трёх узлов а, в и d, потенциалы которых неизвестны:
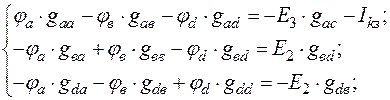 (62)
(62)
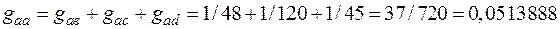
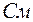 ;
;
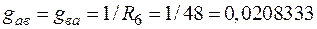
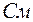 ;
;
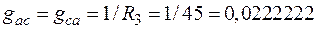
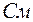 ;
;
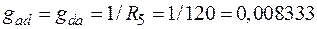
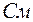 ;
;
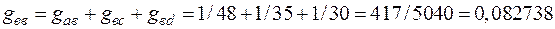
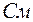 ;
;
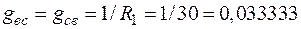
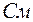 ;
;
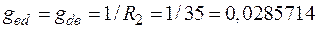
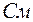 ;
;
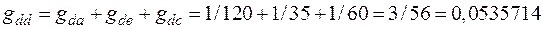
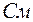 ;
;
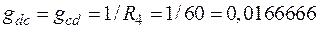
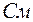 ;
;
 (63)
(63)
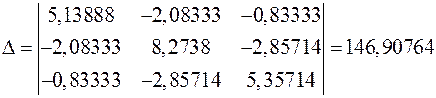
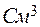 ;
;

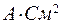 ;
;
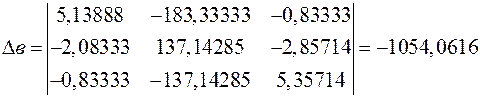
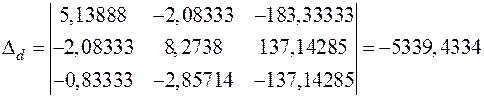
 ;
;
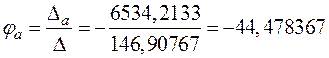
 ;
;
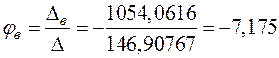
 ;
;
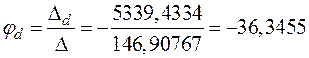
 ;
;
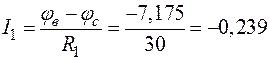

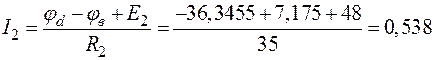
 ;
;
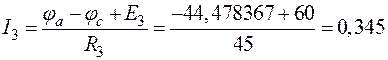
 ;
;
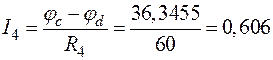
 ;
;
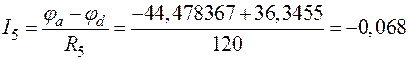
 ;
;
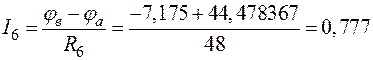
 ;
;
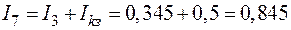
 .
.
Значения токов при расчете по данному методу полностью совпадали со значениями токов, полученными при расчете по методу контурных токов.
Покажем также, что тот же результат получится, если в схеме рис. 18 источник тока 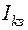 заменить на источник ЭДС Е3 (см. рис. 19).
заменить на источник ЭДС Е3 (см. рис. 19).
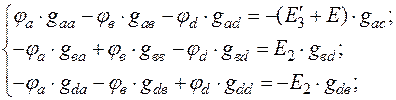 (64)
(64)
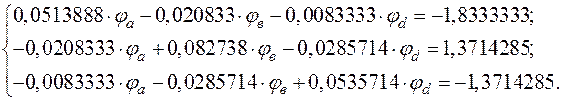 (65)
(65)
Система уравнений (65) имеет точно такой же вид, как и система (63). Следовательно, решение даёт точно такой же результат.
4. Результаты расчета токов, проведённого двумя методами, сведём в табл. 2.
Таблица 2
| Токи, А | I1 | I2 | I3 | I4 | I5 | I6 | I7 |
| Метод контурных токов | -0,239 | 0,538 | 0,345 | 0,606 | -0,068 | 0,777 | 0,845 |
| Метод узловых потенциалов | -0,239 | 0,538 | 0,345 | 0,606 | -0,068 | 0,777 | 0,845 |
5. Составим баланс мощностей в исходной схеме (рис. 18):
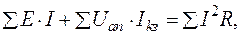 (66)
(66)
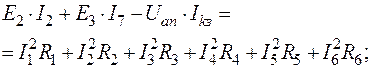 (67)
(67)
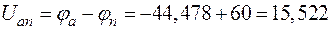
 ;
;
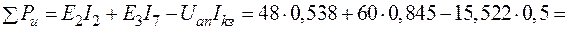
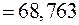
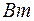 ;
;
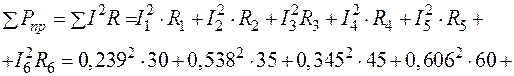
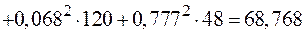
 .
.
Баланс мощностей соблюдается.
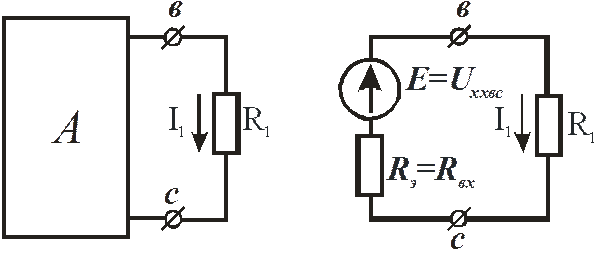
6. Определим ток  по методу активного двухполюсника и эквивалентного генератора.
по методу активного двухполюсника и эквивалентного генератора.
Разомкнём ветвь вс на рис.18. Найдём напряжение холостого хода:
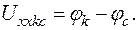 (68)
(68)
Направим контурные токи, как показано на рис. 20:
 (69)
(69)
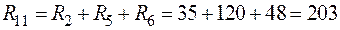
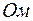 ;
;
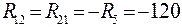
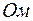 ;
;
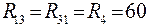
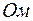 ;
;
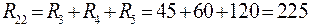
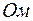 ;
;
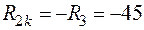
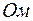 ;
; 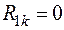
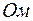 ;
;

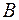 ;
; 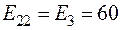
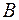 ;
;
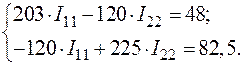 (70)
(70)
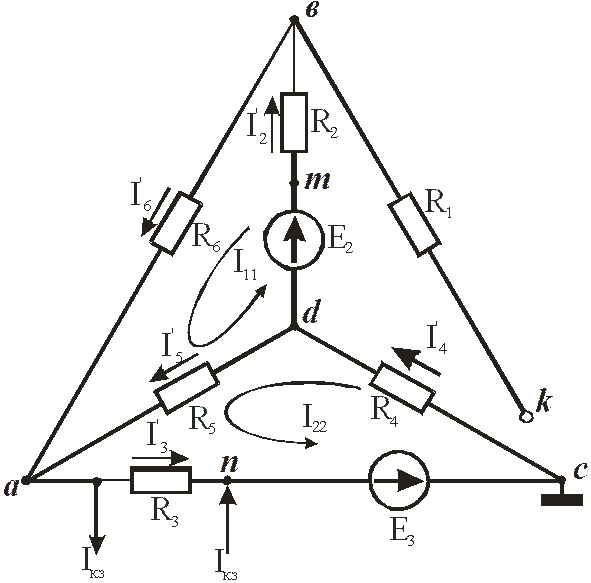
Рис. 20
Решаем эту систему уравнений:I11
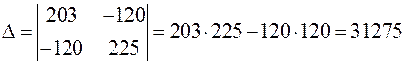
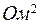 ;
;
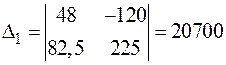
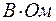 ;
;
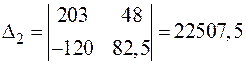
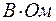 ;
;
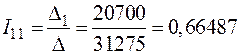
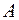 ;
;
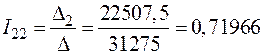
 ;
;
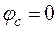
 ;
;
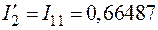
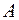 ;
;
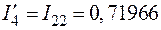
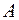 ;
;
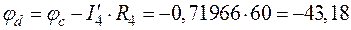
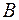 ;
;
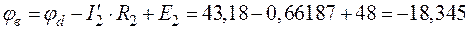
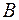 .
.
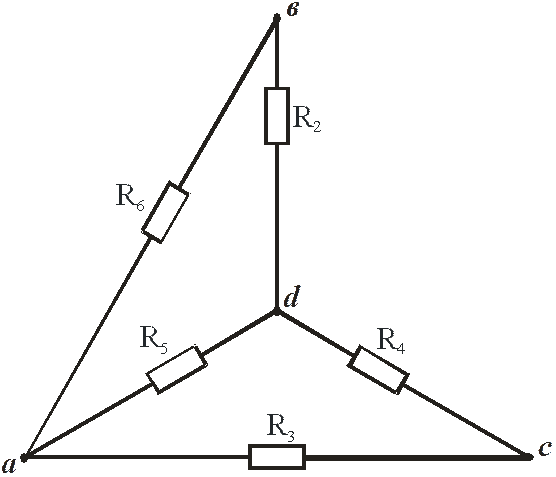
Рис. 24
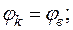
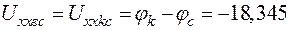
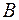 .
.
Найдём эквивалентное сопротивление относительно зажимов схемы, закоротив источники ЭДС (рис. 22).
Преобразуем звезду резисторов R2, R4, R5 в эквивалентный треугольник резисторов (рис. 23):
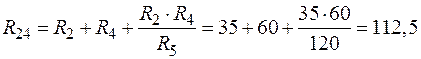
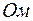 ; (71)
; (71)
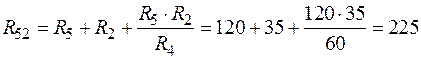
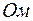 ; (72)
; (72)
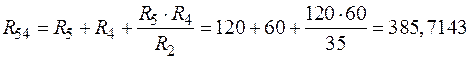
 ; (73)
; (73)
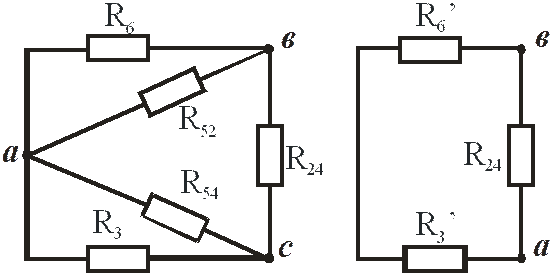
|
|
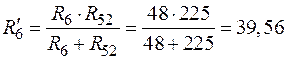
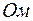 ; (74)
; (74)
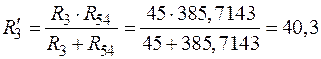
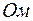 . (75)
. (75)
Найдём входное сопротивление:
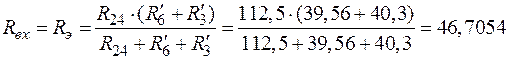
 . (76)
. (76)
|
|
|
Найдём ток I1:
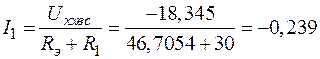
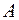 . (77)
. (77)
Значение тока I1 совпадает со значениями, найденными ранее другими методами.
7. Начертим потенциальную диаграмму для контура сdmвanc (рис. 18):
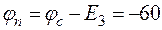
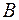 ;
; 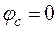
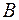 ;
;
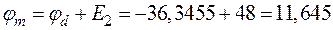
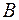 .
.
Остальные потенциалы узлов а, в, с, d возьмём из расчёта по методу узловых потенциалов:
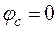
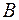 ,
, 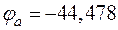
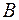 ;
;

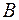 ;
; 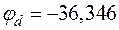
 .
.
На рис. 25 изображена потенциальная диаграмма.
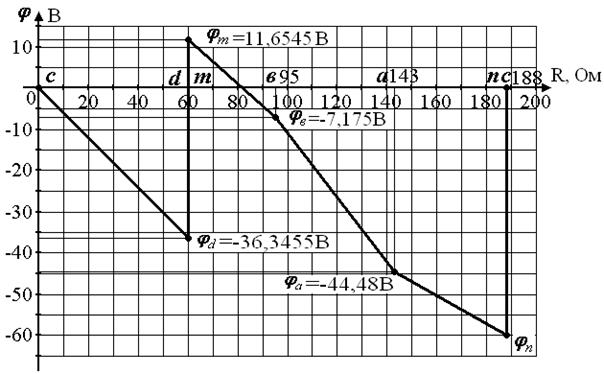
Рис.25
Дата добавления: 2015-07-30; просмотров: 1397;
