Условия задачи

Рассмотрим электрическую цепь, схема которой приведена на рис. 1.1, в которой заданы элементы цепи: источник тока J2=0,8А; источники ЭДС Е21=24В, Е3=30В; резисторы R1=19,5Ом, R2=7,5Ом, R3=3Ом, R41=1Ом, R42=11Ом, R5=16,5Ом, R61=30Ом, R62=90Ом. Необходимо определить токи ветвей цепи, рассчитать баланс мощностей источников и потребителей цепи.

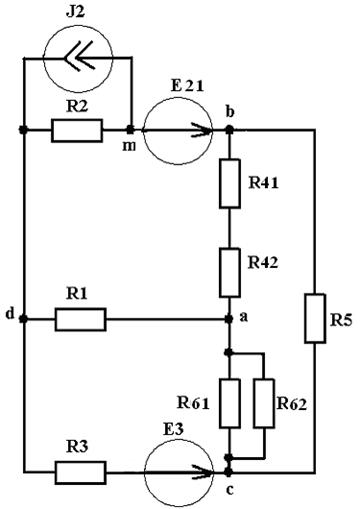
Рис. 1.1

Для решения задачи упростим схему цепи путём преобразования источника тока в эквивалентный источник ЭДС.

Решение задачи производим в среде MATLAB.

Источник ЭДС эквивалентный источнику тока в вольтах:

>> E22 = J2*R2

E22 =

Реальный источник ЭДС в вольтах:

>> E21 = 24;

Эквивалентный источник ЭДС в вольтах:

>> E2 = E21–E22

E2 =

Заменим последовательно и параллельно соединённые резисторы эквивалентными резисторами.

Эквивалентное сопротивление последовательной цепи в омах:

>> R4 = R41+R42

R4 =

Сопротивления параллельной цепи в омах:

>> R61 = 30;

>> R62 = 90;

Эквивалентное сопротивление параллельной цепи в омах:

>> R6 = (R61*R62)/(R61+R62)

R6 =

22.5000

Преобразуем схему путём введениям эквивалентной ЭДС Е2 и эквивалентных сопротивлений R4 и R6, зададимся произвольно направлениями токов ветвей и обходов контуров цепи.

Преобразованная схема приведена на рис. 1.2.

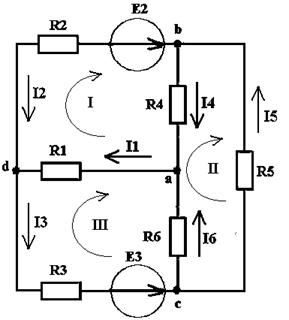
Рис. 1.2

Рассчитаем токи ветвей с использованием законов Кирхгофа, метода контурных токов, метода узловых потенциалов, а также рассчитаем один из токов методом эквивалентного генератора.

1.2. Расчёт токов ветвей с использованием законов Кирхгофа

Количество уравнений цепи, представленной на рис. 1.2, равно количеству ветвей В=6. Количество уравнений по первому закону Кирхгофа равно количеству узлов У–1=3. Количество уравнений по второму закону Кирхгофа равно количеству независимых контуров К=3. Таким образом, необходимо составить систему из шести уравнений: три для узлов a, b, c и три для независимых контуров I, II, III,

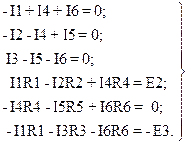
Решаем систему в матричном виде, подставив значения заданных параметров сопротивлений в омах и ЭДС в вольтах:

>> R1 = 19.5;

>> R2 = 7.5;

>> R3 = 3;

>> R4 = 12;

>> R5 = 16.5;

>> R6 = 22.5;

Квадратную матрицу сопротивлений в омах изобразим в виде вектора-строки:

>> R = [-1 0 0 1 0 1;0 -1 0 -1 1 0;0 0 1 0 -1 -1;R1 -R2 0 R4 0 0;0 0 0 -R4 -R5 R6;

-R1 0 -R3 0 0 -R6]

Тогда матрица сопротивлений в омах изобразится в виде:

R =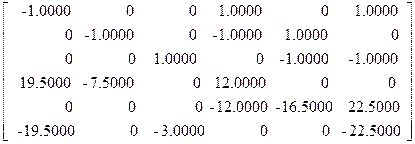

Источники ЭДС в вольтах:

>> E2 = 18;

>> E3=30;

Вектор- столбец ЭДС в вольтах изобразим в виде строки:

>> E=[0;0;0;E2;0;-E3]

Тогда вектор-столбец ЭДС в вольтах изобразится в виде:

E = .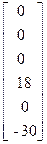

Вектор-столбец токов ветвей определяется функцией инверсии квадратной матрицы сопротивлений помноженной на вектор-столбец ЭДС:

>> I = inv(R)*E

I = .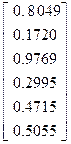

Таким образом, значения токов ветвей цепи в амперах равны:

I1 = 0,8049A, I2 = 0,1720A, I3 = 0,9769A, I4 =0,2995A, I5 = 0,4715A,

I6 = 0,5055A.

1.3. Расчёт баланса мощностей цепи

Суммарная мощность в ваттах источников ЭДС, с учётом того, что источник Е2 работает в режиме потребителя:

>> Pi =(E3*I3)-(E2*I2)

Pi =

26.2110

Суммарная мощность потребителей в ваттах:

>> Pp =I1^(2)*R1+I2^(2)*R2+I3^(2)*R3+I4^(2)*R4+I5^(2)*R5+I6^(2)*R6

Pp =

26.2122

Баланс мощностей с точностью до сотых ватта сходится.