Залежність концентрації вільних носіїв заряду в напівпровідниках від положення рівня Фермі

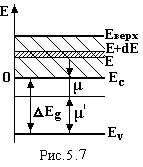Намалюємо енергетичну діаграму напівпровідника (рис.5.5). Енергію будемо відраховувати від дна зони провідності. З рисунка видно, що . Так як електрон-ний газ в напівпровідниках не вироджений, скористаємось повною статистичною функцією розподілу Максвелла-Больцмана по енергіям

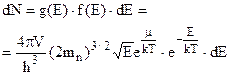
Тоді концентрація електронів в інтервалі енергій від Е до Е+dЕ в зоні провідності буде дорівнювати

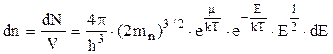. (5.16)

Повна концентрація електронів в зоні провідності при сталій температурі знайдеться шляхом інтегрування (5.16)

.

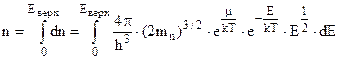Функція 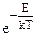із зростанням енергії швидко зменшується. Тому верхню межу інтегрування Е_верх замінено нескінченністю ∞.

.

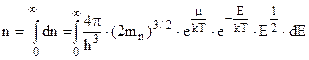Замінюючи 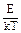=х , маємо

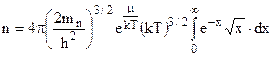. Враховуючи значення табличного інтегралу 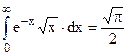, одержуємо концентрацію електронів 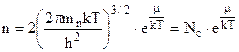. (5.17)

Аналогічно для концентрації дірок маємо

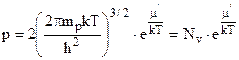. (5.18)

Тут N_C і N_V – ефективна концентрація станів у зоні провідності і у валентній зоні відповідно. Так як μ і μ^I від’ємні (див. рис.5.5) можна зробити висновок: чим далі знаходиться рівень Фермі від границі зони тим менша концентрація відповідних вільних носіїв заряду – електронів у зоні провідності, дірок у валентній зоні. Добуток концентрацій електронів і дірок

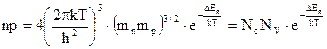(5.19)

не залежить від положення рівня Фермі, а визначається тільки шириною забороненої зони ΔЕ_g і температурою. Це співвідношення називається законом діючих мас.