Сферичний надлишок
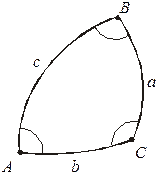
Із сферичної тригонометрії відомо, що сферичний надлишок 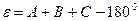 сферичного трикутника
сферичного трикутника 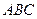 (рис.3.2) рівний площі цього трикутника, якщо радіус сфери, на якій він розташований,
(рис.3.2) рівний площі цього трикутника, якщо радіус сфери, на якій він розташований,  . При
. При 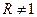 сферичний надлишок визначається формулою
сферичний надлишок визначається формулою
 . (3.1)
. (3.1)
|
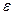 сферичного трикутника будь-якого розміру сферична тригонометрія надає формули різного виду. Серед них:
сферичного трикутника будь-якого розміру сферична тригонометрія надає формули різного виду. Серед них:
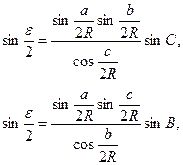
Рис. 3.2
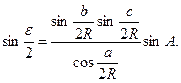
В малих сфероїдних трикутниках 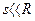 і
і 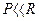 , тому тригонометричні функції малих аргументів можна розкласти в ряди із збереженням тільки перших членів розкладів:
, тому тригонометричні функції малих аргументів можна розкласти в ряди із збереженням тільки перших членів розкладів:
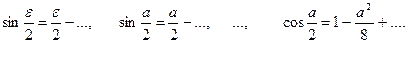
В результаті отримаємо наступні формули:
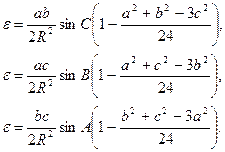 (3.2)
(3.2)
Для типових довжин сторін тріангуляції формули (3.2) можна використовувати без членів в дужках
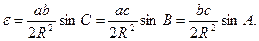 (3.3)
(3.3)
У випадку вимірювання всіх кутів ці формули можна перетворити так, щоб сферичний надлишок 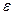 був функцією лише однієї сторони
був функцією лише однієї сторони
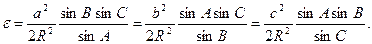 (3.4)
(3.4)
В першокласних геодезичних мережах сферичний надлишок 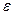 обчислюється з точністю до
обчислюється з точністю до 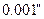 .
.
Для обчислення сферичного надлишку 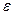 в кожному трикутнику, крім кутів, повинні бути відомі також довжини сторін. Вияснимо, з якою точністю повинні бути відомі довжини сторін і кути, щоб обчислений за ними сферичний надлишок мав похибку не більше
в кожному трикутнику, крім кутів, повинні бути відомі також довжини сторін. Вияснимо, з якою точністю повинні бути відомі довжини сторін і кути, щоб обчислений за ними сферичний надлишок мав похибку не більше 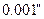 .
.
Для рівностороннього трикутника на основі формул (3.4) можемо записати

Продиференціювавши дану формулу за змінними 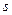 та
та 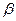 , отримаємо
, отримаємо

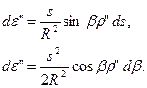
Прийнявши, що  та
та 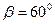 , знайдемо допустимі похибки сторін
, знайдемо допустимі похибки сторін 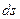 і кутів
і кутів 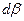 для різних довжин сторін малого сферичного трикутника (табл. 3.1). В табл. 3.1 приведено також можливі значення сферичного надлишку
для різних довжин сторін малого сферичного трикутника (табл. 3.1). В табл. 3.1 приведено також можливі значення сферичного надлишку 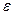 для рівносторонніх трикутників.
для рівносторонніх трикутників.
Одним із основних застосувань сферичного надлишку є виявлення нев’язки 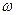 у трикутнику тріангуляції
у трикутнику тріангуляції
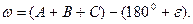 (3.5)
(3.5)
Таблиця 3.1
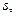 км км
| 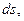 м м
| 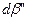
| 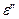
|
Дата добавления: 2015-07-24; просмотров: 1223;