Точність розв'язування головної геодезичної задачі на поверхні еліпсоїда.

При розгляді питання про точність обчислень при розв'язуванні прямої та оберненої геодезичних задач виходять з того, що похибки обчислень ніколи не повинні збільшувати похибки самих вимірювань. В зв'язку з цим всі обчислення виконують з точністю, що в 5-10 раз перевищує досягнуту точність вимірювань. У відповідності з цією точністю повинні підбиратися формули та розроблятися алгоритми обчислень.

Вихідними даними, крім постійних величин (параметрів еліпсоїда, швидкості розповсюдження електромагнітних хвиль у вакуумі тощо), є результати вимірювань довжин ліній та напрямів (кутів).

Враховуючи, що напрями в високоточній тріангуляції отримуються із спостережень з точністю до 0.01", всі обчислення, пов’язані з визначенням геодезичних азимутів виконують з точністю 0.001".

В першокласних мережах довжини сторін вимірюються з похибкою 1:500 000 – 1:000 000, а кути – з похибкою 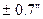. Довжини сторін повинні бути не меншими 20 км.

Похибка взаємного визначення положення пунктів (лінійний зсув кінцевої точки лінії довжиною 20 км), яка викликана похибкою виміряної сторони або похибкою виміряного кута, складе

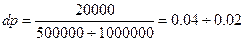м,

м.

Проекції лінійного зсуву на меридіан і паралель будуть відповідно

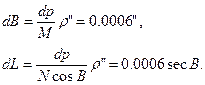
Щоб не допускати накопичення похибок обчислень при послідовному розв'язуванні прямої геодезичної задачі від пункта до пункта, обчислення широт і довгот виконують з точністю до 0.0001".

Слід відмітити, що вказана точність характерна для високоточних геодезичних мереж, що створювались методом тріангуляції. В зв'язку з широким впровадженням сучасних супутникових методів визначення положення пунктів, а також їх використання на відстані до тисяч і більше кілометрів, вимоги щодо точності обчислень можуть бути різними. Відзначимо також і те, що при сучасній обчислювальній техніці мова не йде про технічне досягнення потрібної точності, а про вибір методів та алгоритмів розв'язування геодезичних задач в залежності від заданої точності.