Зв’язки між різними видами координат.

Між просторовими прямокутними (декартовими) 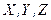та геоцентричними 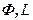координатами, на основі формул (2.10)

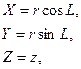
та отриманих співвідношень (2.16), існують прості математичні залежності

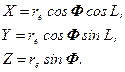(2.28)

Радіус-вектор еліпсоїда 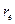визначається із (2.17).

Обернені залежності, на основі (2.28), будуть мати наступний вид

(2.29)

Між просторовими прямокутними координатами X,Y,Z , приведеною широтою и та геодезичною довготою L на основі формул (2.10) та отриманих співвідношень між великою та малою півосями (див. третю формулу (2.5)), існують наступні залежності

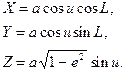(2.30)

Обернені залежності, на основі (2.30), будуть мати наступний вид

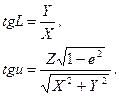(2.31)

Враховуючи співвідношення (2.20) та (2.30), для поверхневих еліпсоїдних координат B,L тадекартових X,Y,Z формули зв'язку мають вид

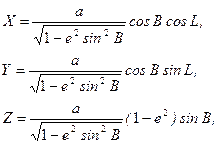
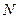Вираз позначимо через і, як буде видно із подальшого викладу (параграф 2.4), це є рівняння для радіуса кривини першого вертикалу заданої точки на поверхні еліпсоїда у функції геодезичної широти. Остаточно, формули зв’язку будуть наступними:

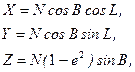(2.32)

Обернені залежності будуть мати наступний вид

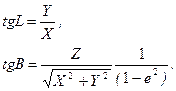(2.33)

Перша формула (2.33) отримана простим перетворенням (шляхом ділення другої формули (2.32) на першу). Друга формула (2.33) отримана наступним чином. Із перших двох формул (2.32) отримаємо

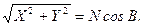
Поділивши третє рівняння (2.32) на отримане, дістанемо остаточно друге рівняння (2.33).

Зв’язок між геодезичними координатами 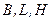та декартовими 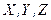отримаємо наступним чином. Спроектуємо висоту 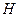(див.рис.1.3) на відповідні осі (рис.1.4). Тоді проекції висоти будуть виражені залежностями

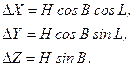
Або

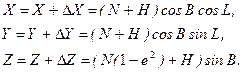(2.34)

Обернені залежності будуть мати наступний вид

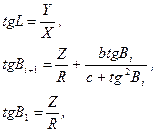
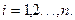(2.35)

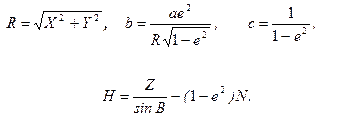
Вираз для обчислення довготи 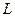знаходимо аналогічно (2.33), а обчислення широти 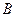, як видно із (2.35) вимагає застосування процесу наближень. Формула для 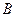отримана наступним чином. На основі рівнянь (2.34), після нескладних перетворень, можемо отримати

,

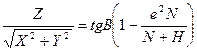а також

.

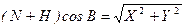Тоді

,

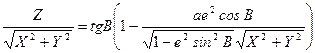або

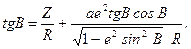(2.36)

Поділимо чисельник і знаменник у другому доданку(2.36) на 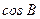і в результаті перетворень отримаємо

,

а домноживши знаменник другого доданку ще на 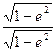та після деяких перетворень, остаточно отримаємо формулу, яка після відповідних позначень буде відповідати (2.35).

Що стосується переходу від поверхневих еліпсоїдних координат B,L до плоских x,y, то вид формул залежить від способу зображення (проекції) поверхні еліпсоїда на площині. Для проекції Гаусса-Крюгера формули зв'язку приведенні при розгляді відповідної теми у розділі 4.