Основи теорії поверхонь.
Геометрію земного еліпсоїда можна розглядати як один із спеціальних розділів теорії поверхонь. Тому в даній книзі багато питань базується на основі цієї теорії. Приведемо найбільш необхідні відомості із теорії поверхонь.
Теорію поверхонь слід розглядати із двох сторін: внутрішньої геометрії поверхні та зовнішньої геометрії. З позиції першої розглядаються властивості, інваріантні відносно викривлення поверхні, а з другої - властивості, інваріантні відносно групи рухів в просторі. Однією з основних задач сфероїдальної геодезії є вивчення внутрішньої геометрії поверхні земного еліпсоїда.
Сукупність таких властивостей поверхні та фігур на ній, які не змінюютьсяпри викривленні поверхні, називається внутрішньою геометрією поверхні.
Викривленням називається таке перетворення поверхні, при якому довжини всіх ліній, що лежать на цій поверхні, зберігаються.
Накладення однієї поверхні на другу після викривлення називається розгортанням першої поверхні на другу.
Поскільки основна увага нами буде звернута на вивчення кривих на поверхні, нагадаємо основні визначення, що відносяться до кривих. Плоскі криві
Рівняння кривої можна задати в наявному виді F(х,у)=0, в явному виді: у=f(х), в параметричному виді x=x(u), y=y(u),u параметр. В залежності від виду заданої кривої диференціал дуги знаходять із виразів:
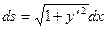 , де
, де 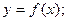 (1.1)
(1.1)
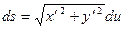 , де
, де 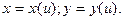
Кривиною К плоскої кривої в даній точці Q називається границя відношення кута між дотичними в двох суміжних точках Q1 і Q2 до дуги кривої між цими точками при зменшенні дуги до нескінченно малих розмірів.
Рис. 1.2
Радіусом кривини R вданій точці називається величина, обернена кривині
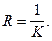
Кривина та радіус кривини плоскої кривої визначаються за формулами:
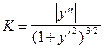
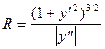 , де
, де 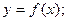
та
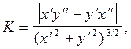
 , де
, де 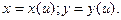
Просторові криві.
Рівняння просторової кривої в параметричному виді
х=х(и), у=у(и), 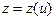 , де u - параметр.
, де u - параметр.
Диференціал дуги просторової кривої
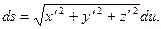
В кожній точці, Q просторової кривої визначаються три прямі і три площини, що взаємно перетинаються в т.Q під прямими кутами (рис .1.3).
Прямі. Дотична, що є граничним положенням січної. Головна нормаль - перетин нормальної і стичної площин, бінормаль- пряма, перпендикулярна до стичної площини Площини. Нормальна площина - площина, перпендикулярна до дотичної. Стична площина—граничне положення площини, що проходить через три близькі .точки кривої Q1Q2 та Q3 коли Q1 ® Q2 і Q3 ® Q2 (рис-1.х). Спрямна площина - площина, що містить дотичну і бінормаль.
Кривиною просторової кривої в даній точці називається числова характеристика відхилення кривої від прямої лінії в області даної точки кривої, її обчислюють за формулою
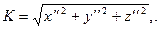
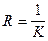
Крученням просторової кривої в даній точці називається числова характеристика відхилення просторової кривої від плоскої кривої в області даної точки.
Поверхні. Рівняння поверхні задається наступними формами;
F(х, у, z)=0 - неявна
z = f(x, у) - явна
x=x(u, v), y=y(u, v), z=z(и, v) -параметрична.
Диференціал дуги або лінійний елемент поверхні
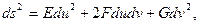 (1.4)
(1.4)
де
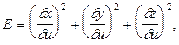 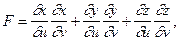
|
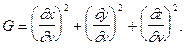
Праву частину рівняння (1.4) називають першою квадратичною формою поверхні. Коефіцієнти E, F, G, що є функціями координат u та v, залежать тільки від положеня: точки на поверхні. Через дані коефіцієнти можна виразити також кут між кривими та площі фігур, тобто перша квадратична форма визначає метрику поверхні. При вигинанні поверхні без розтягів та розривів її рівняння звичайно змінюється, але метрика залишиться тією ж, тобто перша квадратична форма при вигинанні поверхні зберігається.
В сфероїдальній геодезії застосовується ортогональна система криволінійних параметричних координат, які утворюють на поверхні прямокутну сітку координат. В такому випадку рівняння (1.4) прийме наступний вид:
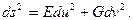 (1.5)
(1.5)
Позначивши 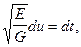 отримаєм
отримаєм
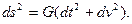 (1.6)
(1.6)
Криволінійні координати (t,v) називаються ізометричними координатами.
Важливе значення у сфероїдальній геодезії мають нормальні перерізи.Вони отримуються від перетину поверхні площиною, що проходить через нормаль поверхні. Такі. площини, як було вже вище сказано, називаються нормальними.
В теорії поверхонь доказується, що всі криві на поверхні, які проходять через задану точку в одному і тому ж напрямі (тобто які мають спільну дотичну) і які мають спільну стичну площину, мають в цій точці одинакову кривину К . Відповідно, кривина довільної кривої рівна, кривині плоского перерізу, що є слідом перетину поверхні стичною площиною даної кривої.
Якщо позначити радіус кривини кривої, у якої головна нормаль збігаеться з нормаллю до поверхні через й R0 , тоді радіус кривини якої завгодно кривої на поверхні буде визначатися згідно формули:
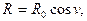 (1.7)
(1.7)
де v - кут, утворений головною нормаллю кривої та нормаллю до поверхні. Формула (1.7) виражає відому теорему Меньє:
Радіус кривини якої завгодно кривої на поверхні рівний радіусу кривини нормального перерізу ,що має з нею спільну дотичну, помноженому на косінус кута між нормаллю до поверхні та головною нормаалю кривої.
Величина 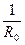 називається ще нормальною кривиною. Для її визначення служить наступна формула:
називається ще нормальною кривиною. Для її визначення служить наступна формула:
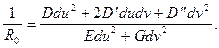 (1.8)
(1.8)
Вираз, що знаходиться в чисельнику, називається другою квадратичноюформою поверхні. Величини D, D’,D’’ називаються коефіцієнтами другої квадратичної форми.
Через кожну точку поверхні можна провести цілу низку нормальних площин і, таким чином, отримати цілий ряд нормальних перерізів. Із нормальних перерізів суттєве значення мають два головних взаємно перпендикулярних перерізи: один з найбільшою
кривиною 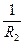 та другий: з найменшою
та другий: з найменшою 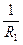 Кривину будь-якого нормального перерізу можна виразити через кривину головних перерізів за формулою Ейлера
Кривину будь-якого нормального перерізу можна виразити через кривину головних перерізів за формулою Ейлера
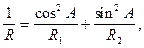 (1.9)
(1.9)
де А - азимут даного нормального перерізу.
Крім кривини нормального перерізу, в сфероїдальній геодезії використовується Гауссова кривина
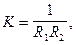
а величина
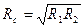 (1.10)
(1.10)
носить назву середнього радіуса, кривини.
В нормального перерізу хоча б в одній точці головна нормаль збігається з нормаллю до поверхні. Ця точка називається геодезичною точкою. В геодезичній точці. нормального перерізу кут v рівний нулю. Відповідно, нормальна кривина рівна кривині нормального перерізу в його геодезичній точці. Криву на поверхні, в якої всі точки геодезичні, тобто головна нормаль збігається з нормаллю до поверхні у всіх точках, називають геодезичною лінією. Геодезичні лінії на поверхні відіграють роль прямих на площині, тому багато положень диференціальної геометрії на площині можуть бути узагальнені для поверхонь з заміною прямих геодезичними.
1.5. Чисельні методи у сфероїдальній геодезії.
Ще в недалекому минулому всі обчислення в області сфероїдальної геодезії виконувались з допомогою логарифмів, а пізніше з допомогою малопотужної обчислювальної техніки. При обчисленнях приходилось користуватися об'ємними таблицями тригонометричних функцій та багаточисельними таблицями різноманітних величин, що в основному залежали від широти.
В сучасних умовах, коли ми майже всі масові обчислення виконуються на ЕОМ, абсолютно відпала необхідність в складанні спеціальних таблиць для геодезичних обчислень. Достатньо мати лише обмежене число постійних величин, необхідних для розв'язку тої чи іншої задачі. Прогрес обчислювальних методів з використанням сучасних програмних засобів дозволяє навіть обмежитись записом формул в самому загальному виді, іноді тільки у виді диференціальних рівнянь, а подальші перетворення віднести безпосередньо до процесу роботи на комп'ютері.
Характерним прикладом вибору обчислювальних методів на ЕОМ є застосування чисельних методів для розв'язку диференціальних рівнянь і обчислення еліптичних інтегралів. Такі методи були відомі давно, але на практиці не застосовувались, поскільки були досить трудомісткі і складні для ручних обчислень. Алгоритмів, якими користуються в сучасних чисельних методах дуже багато. Якщо їх реалізувати у вигляді достатньо універсальних програм, то вони можуть стати базовими і слугувати основою сучасних геодезичних технологій.
При розв'язку задач сфероїдальної геодезії приходиться мати справу з наступними обчислювальними задачами:
· апроксимація функцій (поліномінальна, дробово-раціональна),
· чисельне інтегрування (квадратурні формули Гаусса, Чебишева),
· чисельні методи розв'язку диференційних рівнянь з початковими умовами (методи Рунге - Кутта).
Апроксимація функцій (наближення) - це заміщення різноманітних функцій "близькими" до них. більш зручними для використання функціями. До задач апроксимації функцій з параметрами, що входять лінійно, відносяться задачі апроксимації поліномами, а з параметрами, що входять нелінійно -- дробово-раціональні апроксимації. Наближене представлення неперервної функції з допомогою полінома степені п можна отримати з допомогою ряда Тейлора та. цілої низки його модифікацій, а одним із найбільш ефективних методів отримання необхідного числа дробово-раціональних наближень заданої функції є метод ланцюгових дробів.
Приклади апроксимації функції, що мають застосування в сфероїдальній геодезії, будуть наведені в кінці даної книги. Ми лише відмітимо, що безпосереднє отримання коефіцієнтів цих функцій зв'язане з довгими алгебраїчними обчисленнями і на данийчас такий шлях не є ефективним, поскільки простіше виконати обчислення із заданою функцією.
Наближене обчислення визначеного інтеграла можна проводити різними методами: Сімпсона, Гаусса, Чебишева, Ромберга тощо. Розглянемо коротко тільки деякі з них.
Для обчислення інтеграла
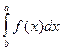
методом Сімпсона інтервал інтегрування ділить на п рівних частин (п - парне число).
Для кожної вузлової точки k (k=0,1,2,...,n) з кроком  за аргументом
за аргументом 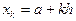
обчислюють значення підінтегральної функції 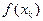 . Після цього визначений інтеграл може бути обчислений за формулою
. Після цього визначений інтеграл може бути обчислений за формулою
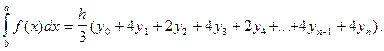 (1.11)
(1.11)
За Гаусом наближене обчислення визначеного інтеграла полягає в наступному. В проміжку між граничними .знажннями аргументів х=а і х =b вибирають п. вузлових точок за рівнянням
 ,
,
де vi, - деяке постійне число менше одиниці, віднесене до відповідної вузлової точки. Для кожної вузлової точки за аргументом хі обчислюють значення підінтегральної функції, яке потім домножують на деяке постійне число що відповідає цій точці.
Значення постійна Rt в залежності від n
| n=1 | v1=0.5 | R1=1 |
| n=2 | v1=1-v2=0.21132487 | R1=R2=0.5 |
| n=3 | v1=1-v3=0.1127016654 v2=0.5 | R1=R3=0.2777777778 R3=0.4444444444 |
| n=4 | v1=1-v4=0.0694318442 v2=1-v3=0.3300094782 | R1=R4=0.1739274226 R2=R3=0.3260725774 |
| n=5 | v1=1-v5=0.0469100770 v2=1-v4=0.2307653449 v3=0.5 | R1=R5=0.1184634425 R2=R4=0.2393143352 R3=0.2844444444 |
| n=6 | v1=1-v6=0.0337652429 v2=1-v5=0.1693953068 v3=1-v4=0.3806904070 | R1=R6=0.0856622462 R2=R5=0.1803807865 R3=R4=0.2339569673 |
Значення інтеграла можна обчислити за наступною формулою:
 (1.12)
(1.12)
права частина якої тим ближча до точного значення інтегралу, чим більше використовується вузлових точок.
Методи Рунге-Кутта належать до багатоточкових однокрокових методів чисельного інтегрування систем звичайних диференційних рівнянь. Суть методу Рунге-Кутта полягає в наступному. Нехай функція визначається диференційним рівнянням
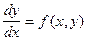
та початковими значеннями у=у0 при х=х0. Слід знайти чисельне значення функції
уn для заданого значення аргумента
Для визначення уn послідовно обчислюють значення функцій уі для рівновіддалених проміжних значень xi=x0+hi (I=1,2,…n) причому за початкові приймають значення xi-1 I yn-1, знайдені в попередньому обчислені. Прирісі аргумента 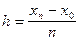 є кроком інтегрування величина якого встановлюєіься в залежності від заданої точності визначення функції Функцію yi обчислюють за формулою
є кроком інтегрування величина якого встановлюєіься в залежності від заданої точності визначення функції Функцію yi обчислюють за формулою
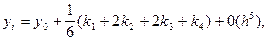 (1.13)
(1.13)
де
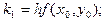
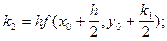
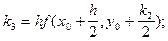 (1.14)
(1.14)
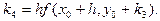
позначення 0(hk) свідчить про те, що у формулах знехтувано доданками порядку hk.
При виводі цих формул вихідним рівнянням послужив розклад функції yi в ряд Тейлора за степенями h до четвертого порядку.
Для розв'язування системи звичайних диференційних рівнянь
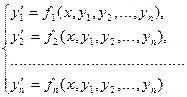
будується система рівновіддалених точок xi=x0+ih . Обчислення уji в кожній точці здійснюється за формулою
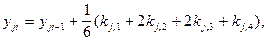 (1.15)
(1.15)
де j - номер рівняння системи, і - номер точки інтегрування. Коефіцієнти kji
визначаються за формулами, аналогічними (1.14).
Класичний метод Рунге-Кутта частково модифікувався для практичних застосувань (в основному для прискорення та спрощення процесу обчислень). Найбільш відомі модифікації Мерсона (1958) та Інгланда (19..). На даному рівні розвитку обчислювальних засобів особливого виграшу ці модифікації не дають, а отже класичний метод Рунге-Кутта залишається базовим методом чисельного інтегрування диференційних рівнянь першого порядку.
Дата добавления: 2015-07-24; просмотров: 1041;
