Сравнительный анализ систем (правило САС)

Если нужно определить, с чем связаны различия в функционировании двух систем, следует применить правило АСС или АСФ поочередно к каждой из систем, затем произвести их сравнение и найти элемент, особенности которого определяют различия систем в целом.

Это правило проще всего проиллюстрировать на уже рассмотренном примере 4.1. Для этого несколько изменим вопрос задачи.

Пример 4.7. Почему в мякотных волокнах даже малого диаметра возбуждение распространяется достаточно быстро по сравнению с более, толстыми безмякотными волокнами?

Ответ. Нужно сравнить функционирование двух систем – «мякотное волокно» и «безмякотное волокно». Применяем правило САС. Какой элемент обеспечивает распространение потенциала действия вдоль любого волокна? Это «местный ток», возникающий между возбужденным и невозбужденным участками. Отличается ли этот элемент в рассматриваемых системах? Да. В безмякотном волокне указанные участки находятся рядом, а в мякотном – на некотором расстоянии друг от друга, так как местный ток может пройти через мембрану волокна только там, где отсутствует миелиновая оболочка т. е., в перехватах Ранвье. Поэтому в мякотных волокнах возбуждение движется скачками, сальтаторно – от перехвата к перехвату, что и определяет более быстрое распространение.

Аналогичным образом применяется правило САС и в других задачах, где требуется сравнить две системы.

Следующее и последнее правило имеет очень широкое применение. Его можно эффективно использовать не только в физиологии, но и во многих других областях. Это правило позволяет успешно решать самые различные задачи, сущность которых сводится к следующему. Нужно предсказать или объяснить результат взаимодействия каких-либо систем. В частности, и это очень важная особенность данного правила, объяснить различия результатов, получаемых при взаимодействии разных систем.

Сущность правила вытекает из его названия АРР-ВС анализ различных результатов взаимодействия систем. Прежде чем сформулировать правило и перейти к примерам его использования, введем необходимые термины.

Взаимодействие систем будем называть их пересечением, а сами системы – пересекающимися. На рис. 4.4 изображены пересекающиеся и непересекающиеся системы. Из него видно, что системы не могут

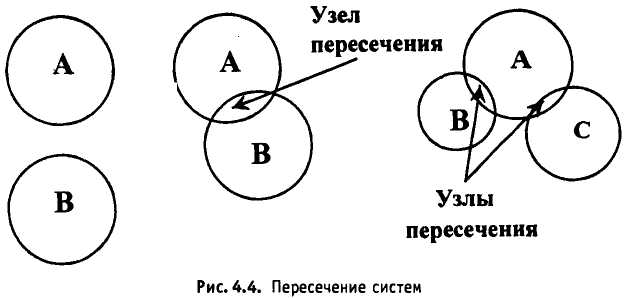
взаимодействовать всеми своими элементами. Пересечение затрагивает ограниченное их число. Во многих случаях его можно свести всего к двум – по одному элементу из каждой системы. Участок, в котором происходит пересечение, назовем узлом пересечения. Это – основной пункт в применении правила АРР-ВС. Как Вы увидите в дальнейшем, именно анализ узлов пересечения позволяет успешно решать многие задачи. Поэтому остановимся на данном понятии более подробно.

Рассмотрим простой пример. Допустим, на столе лежат рядом тетрадь и шариковая ручка. Обе эти системы взаимодействуют с системой «стол», так как оказывают на него некоторое давление. Но величина этого давления настолько мала, что данное взаимодействие (пересечение) систем не представляет для нас никакого интереса. Между собой же системы «ручка» и «тетрадь» пока никак не взаимодействуют и, следовательно, не пересекаются. Но, если мы начнем писать в тетради, то теперь системы станут пересекающимися. При этом понятно, что в пересечении участвуют далеко не все элементы. Например, обложка тетради и колпачок ручки никакого отношению к появлению на бумаге букв не имеют. В узле пересечения от системы «ручка» участвует элемент «шарик с пастой», а от системы «тетрадь» – элемент «участок бумаги под шариком».

Если ручка вдруг перестала писать, иначе говоря взаимодействие систем изменилось, то для выяснения причины этого мы будем анализировать только узел пересечения. Возможно, что на шарике больше нет пасты, или он «присох» или на участке бумаги под шариком оказалось жировое пятно. Главное – это то, что нарушение или изменение взаимодействия систем может быть связано только с какими-то изменениями в узлах пересечения.

Примечание.Если строго придерживаться упоминавшейся выше терминологии, то «ручка» и «тетрадь» – это квазисистемы. Но на логику рассуждений данное обстоятельство никак не влияет. Поэтому еще раз напомним, что в дальнейшем для облегчения восприятия будем использовать общий термин «система» применительно ко всем ситуациям, которые будут встречаться в решаемых задачах.

Теперь можно перейти к рассмотрению применения правила АРР-ВС. Взаимодействие систем встречается в нескольких вариантах.

Вариант 1-1. Одна система взаимодействует с другой. Например, система «надпочечник» выделяет адреналин, который оказывает влияние на работу системы «сердце». В зависимости от состояния этих систем результаты их пересечения могут быть различными.

Вариант 2-1. Две системы независимо друг от друга воздействуют на третью систему. При этом в каждом случае результаты пересечения систем оказываются различными. Например, если взять свежую кровь и одну ее порцию поместить в обычную пробирку, а другую в пробирку, стенки которой покрыты парафином, то во второй пробирке свертывание будет происходить медленней, чем в первой. Здесь две системы – «стеклянная пробирка» и «парафиновая пробирка» по-разному взаимодействуют с системой «кровь».

Вариант 1-2. Одна система воздействует на две других. Например, изучают влияние высокой температуры среды на организм. Если мы поместим в тепловую камеру двух собак, то система «тепловая камера» будет одновременно пересекаться с системой «первая собака» и системой «вторая собака». Если состояние собак различно, то будут различаться и полученные, результаты.

В последнем случае одна система воздействовала на две других одновременно. Возможна и другая ситуация – одна система последовательно воздействует на другую систему, причем эта последняя в каждом случае находится в разных состояниях. Таким образом вариант 1-2 может иметь два подварианта. Например, если медсестра утром делает инъекцию одного и того же препарата двум больным, – это первый подвариант. Если инъекцию делают одному и тому же больному, но сначала утром, а потом вечером, то это второй подвариант.

Теперь можно, наконец, сформулировать правило АРР-ВС.