Модели ядра

Сложный характер ядерных сил и трудность точного решения уравнений движения всех нуклонов ядра не позволили до настоящего времени разработать единую последовательную теорию атомного ядра. Поэтому на данном этапе прибегают к рассмотрению приближённых ядерных моделей, в которых реальное ядро заменяется некоторой модельной системой, хорошо описывающей только определённые свойства ядра.

Рассмотрим некоторые из большого числа существующих моделей ядра.

Капельная модель ядра (1936 г., Н. Бор и Я.Н. Френкель).

Малый радиус действия ядерных сил и примерное постоянство средней удельной энергии связи позволяет уподобить ядро капельке жидкости. Модель основана на аналогии между поведением нуклонов в ядре и поведением молекул в капле жидкости:

а) ядерным силам (как и межмолекулярным) свойственно насыщение и короткодействие;

б) ядро (как и капля жидкости) характеризуется практически постоянной плотностью, не зависящей от числа нуклонов;

в) объём ядра, как и объём капли, пропорционален числу частиц;

г) энергия связи нуклонов, расположенных на поверхности ядра, меньше, чем у внутренних нуклонов, так как у них меньше соседей, с которыми они взаимодействуют. Это приводит к стремлению ядра-капли принять сферическую форму, при которой его поверхность была бы минимальна (при данном объеме) - поверхность ядра стягивается силами поверхностного натяжения. Таким образом, картина подобна той, которая имеет место в капле жидкости.

Существенное отличие ядра от капли обычной жидкости в этой модели заключается в том, что ядро трактуется как капля электрически заряженной жидкости, подчиняющаяся законам квантовой механики. Кроме внутренних движений нуклонов, возможны и коллективные движения отдельных частей капли друг относительно друга, приводящие к деформации ядра. Эти деформации объясняют возможность деления ядра-капли, открытую впоследствии.

Капельная модель ядра позволила получить полуэмпирическую формулу для энергии связи нуклонов в ядре, объяснила механизм ядерных реакций (в частности, реакции деления ядер).

Оболочечная модель ядра была развита в работах М. Гепперт - Майер и Иенсена.

Ядро имеет очень много свойств, которые проще объяснять, основываясь на картине независимого движения нуклонов в нём, чем на представлении о движении сильно взаимодействующих нуклонов, как предполагается в модели жидкой капли.

Бартлет и Эльзасер первыми (1932-1934 г.г.) обратили внимание на то, что ядра обладают особой устойчивостью, когда Z или N (или оба эти числа) равно одному из «магических чисел»:

2, 8, 20, 28, 50, 82, 126.

Магические числа указывали на то, что в ядрах, так же как и в атомах, имеются оболочки. В простой модели ядерных оболочек предполагается, что нуклоны движутся независимо друг от друга в сферически-симметричном потенциале ядра; дискретные энергетические уровни (оболочки) заполняются нуклонами согласно принципу Паули. Заполненные оболочки должны быть сферически - симметричными, иметь полный момент количества движения, равный нулю, и обладать повышенной стабильностью. Устойчивую оболочку трудно возбудить, и поэтому первое её возбуждённое состояние должно лежать довольно высоко по энергии, что подтверждается экспериментально.

Самыми устойчивыми являются дважды магические ядра, их всего пять: 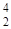He (Z=N=2), 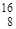O (Z=N=8), 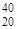Ca (Z=N=20), 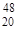Ca (Z=20, N=28) и 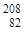Pb (Z=82, N=126).

Все более тяжёлые ядра уже радиоактивны, т.е. неустойчивы. Оболочечная модель позволила объяснить магические числа, спины и магнитные моменты ядер, их разную устойчивость, периодичность изменений их свойств. Особенно хорошо она объясняет свойства ядер, близких к магическим.

Позже возникла обобщённая модель ядра, вобравшая в себя все сильные стороны оболочечной и капельной моделей. Существуют и другие модели ядра: оптическая (объясняет взаимодействие ядер с налетающими частицами), ротационная, вибрационная и т.д.