ЭЛЕКТРОННО-ДЫРОЧНЫЙ ПЕРЕХОД В НЕРАВНОВЕСНОМ СОСТОЯНИИ

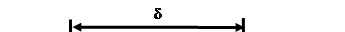
Если к р-n структуре приложить внешнее напряжение, то динамическое равновесие между диффузионными и дрейфовыми токами нарушится и через структуру потечет электрический ток. Покажем, что величина и направление результирующего тока зависит от величины и полярности приложенного к р-n структуре напряжения.

Приложим к р-n структуре напряжение плюсом к р- области, а минусом к n- области (рис. 8.16 а).

Напряжение такой полярности называют прямым U_пр, оно противоположно по полярности контактной разности потенциалов и поэтому снижает потенциальный барьер, препятствующий переходу основных носителей в области, где они являются неосновными.

Как отмечалось ранее, р-n переход обладает более высоким сопротивлением, чем р- и n – области структуры. Поэтому приближенно будем считать, что все внешнее напряжение приложено к переходу и разность потенциалов в области р-n переходе уменьшается до величины (рис. 8.16 б).

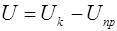. (8.50)

Под влиянием прямого внешнего напряжения основные носители заряда смещаются вглубь перехода и при согласно выражениям (8.49) и (8.50) толщина р-n перехода уменьшается до размера

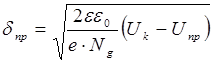. (8.51)

Сужение р-n перехода в основном происходит за счет менее легированной n- области (рис. 8.16 а).

Внешнее напряжение уменьшает потенциал области положительного заряда и увеличивает потенциал области отрицательного заряда в р-n переходе (рис. 8.16 б), за счет чего в соответствии с выражениями (8.26) и (8.27) возрастает поток основных носителей заряда, способных преодолеть снизившийся потенциальный барьер
(рис. 8. 16 а). Следовательно, в n- область войдет дополнительное количество дырок, а в р- область – электронов. Введение носителей заряда через р-n переход при прямом напряжении в области, где они являются неосновными, называется инжекцией.

Оценим приращение концентрации дырок при их инжекции в n –область с помощью выражения (8.26). Из этого выражения следует, что в состоянии равновесия концентрация дырок на границе р-n перехода и n- области (точка х₂ рис. 8.16 в), где
φ = φ_n и P = P_n, равна:

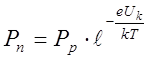. (8.52)

При уменьшении потенциального барьера до величины (8.50) концентрация дырок на границе р-n перехода и n –области (точка x₁ на рис. 8.16 в) возрастет до значения

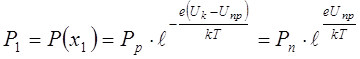. (8.53)

Из формулы (8.53) следует, что концентрация инжектированных дырок зависит от равновесной концентрации дырок в n-области и U_пр, а от параметров р-области не зависит.

Аналогичный расчет для инжектированных электронов в р- область приводит к выражению (рис. 8.16 в)

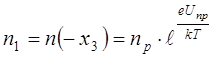. (8.54)

Приращение концентрации дырок в n- области на границе с переходом равно

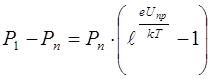. (8.55)

За счет приращения концентрации дырок возникает диффузионный процесс, приводящий к проникновению дырок в глубь n- области, где они являются неосновными носителями. Зависимость концентрации инжектированных дырок за переходом от расстояния можно найти, решив уравнение непрерывности (7.82) для n- области. Учтем, что рассматривается установившийся процесс ( 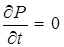), электрическое поле за пределами перехода пренебрежимо мало (Е =0) и генерация свободных носителей за счет внешнего источника отсутствует (g_p = 0). В этом приближении уравнение (7.82) принимает вид:

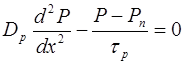. (8.56)

Это уравнение имеет следующее общее решение:

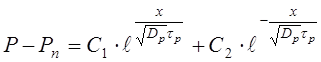. (8.57)

Постоянные C₁ и C₂ определим из граничных условий. Выберем начало отсчета x на границе р-n перехода и n – области (точка x₁ на рис. 8.16 в).

Тогда при x = x₁ = 0 в соответствии с выражением (8.53)

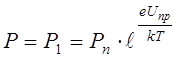. (8.58)

При x → ∞ P → P_n, поэтому C₁ =0.

Из равенства (8.57) следует, что

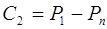. (8.59)

Таким образом, решение уравнения (8.56) имеет вид

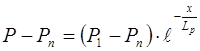, (8.60)

где 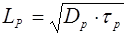. (8.61)

Величина L_P, как отмечалось в § 7.5., называется диффузионной длиной неосновных носителей заряда (дырок). Как следует из решения (8.60) на расстоянии x=L_P избыточная над равновесной концентрация дырок убывает в 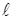раз.

Найдем градиент концентрации дырок за р-n переходом. Для этого продифференцируем функцию (8.60) по х.

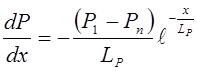. (8.49)

Инжектированные в n – область дырки по мере приближения к отрицательному выводу рекомбинируют с электронами, в связи с чем концентрация дырок убывает и приближается к стационарному значению n_p (рис. 8.16 в).

Найдем плотность диффузионного тока, вызванного градиентом концентрации дырок (8.62)

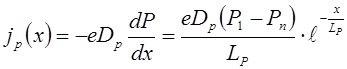. (8.63)

Из выражения (8.63) следует, что плотность диффузионного тока дырок уменьшается от максимального значения при x = x₁ =0, равного с учетом формулы (8.55)

, (8.64)

до нуля на расстоянии нескольких L_p от перехода.

Инжекция дырок в n – область вызывает поступление из внешней цепи такого же количества электронов, благодаря чему поддерживается нейтральность n – области.

Одновременно с инжекцией дырок в n- область происходит инжекция электронов в р-область.

Расчет, аналогичный проведенному расчету для j_p, приводит к выражению для плотности тока инжекции электронов на границе р-n перехода и р- области

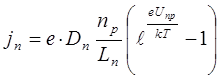. (8.65)

Для определения результирующей плотности прямого тока через р-n переход необходимо сложить дырочную и электронную составляющие в одном из сечений структуры. Если считать что δ << L_P, L_n, то рекомбинацией и генерацией носителей внутри перехода можно пренебречь. В этом случае j_n и j_p остаются постоянными в области р-n перехода, поэтому для нахождения результирующей плотности прямого тока можно просуммировать выражения (8.64) и (8.65), определенные на разных границах р-n перехода

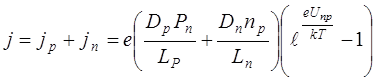. (8.66)

Подадим на р-n структуру внешнее напряжение совпадающее по полярности с контактной разностью потенциалов (рис. 8.17 а).

Потенциальный барьер на переходе возрастает до величины 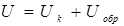(рис. 8.17 б), что вызовет резкое уменьшение числа основных носителей способных его преодолеть. Основные носители оттесняются от перехода, и его толщина увеличивается в соответствии с выражением

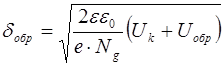. (8.67)

Электрическое поле в переходе способствует втягиванию неосновных носителей через переход в области, где они являются основными.

Так, как неосновные носители заряда создают результирующий ток, направление которого противоположно прямому току, его называют обратным током. Напряжение, вызвавшее этот ток, называют обратным напряжением. У границ перехода концентрация неосновных носителей заряда становится меньше равновесной
(рис. 8.17 в), за счет чего возникают диффузионные потоки дырок в n- области и электронов в р- области к границам р-n перехода (рис. 8.17 а).

Явление вытягивания из р- и
n –областей р-n структуры неосновных носителей заряда к границам р-n перехода при обратном напряжении и перенос их в области, где они являются основными, называется .

В образовании тока экстракции могут участвовать только те неосновные носители заряда, которые генерируются на расстоянии L_P в n- области и L_n в р- области.

Найдем зависимость концентрации дырок за р-n переходом в n- области от расстояния х, отсчитываемого от точки х₃ на рис. 8.17 в в направлении к границе перехода. Учтем, что в условиях равновесия концентрация дырок на границе перехода определяется выражением (8.52). При обратном напряжении на переходе концентрация дырок на границе уменьшится до значения

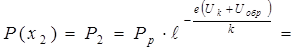
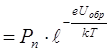. (8.68)

Убыль концентрации дырок на границе перехода равна

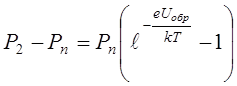. (8.69)

Зависимость концентрации дырок от расстояния находится из общего решения (8.57) уравнения диффузии (8.56) с учетом граничных условий 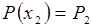и

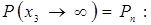
. (8.70)

Продифференцируем выражение (8.70) по х и найдем градиент концентрации дырок

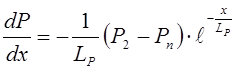. (8.71)

Плотность тока экстракции с учетом (8.70) равна

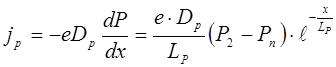. (8.72)

Учтем выражение (8.69) и, положив в (8.72) х = х₃ = 0, найдем максимальное значение плотности экстракции дырок

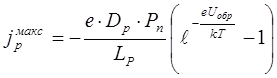. (8.73)

При комнатной температуре и обратном напряжении ~ 0,1 В экспонента значительно меньше 1, поэтому выражение (8.73) можно записать в виде:

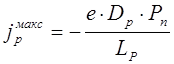. (8.74)

Проводя аналогичные расчеты для максимального значения плотности тока экстракции электронов можно получить выражение

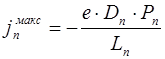. (8.75)

Полагая, что практически все генерируемые вблизи границ перехода неосновные носители переносятся через переход, максимальную результирующую плотность тока экстракции найдем, сложив выражения (8.73) и (8.75)

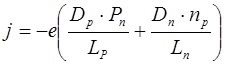. (8.76)

Так как концентрации неосновных носителей значительно меньше, чем основных, ток экстракции через переход намного меньше прямого тока.

Поскольку напряжение не влияет на скорость генерации основных носителей заряда, ток экстракции считать током насыщения.

Неосновные носители заряда образуются за счет термогенерации, поэтому ток экстракции еще называют тепловым током.