ЭЛЕКТРОННО-ДЫРОЧНЫЙ ПЕРЕХОД В СОСТОЯНИИ РАВНОВЕСИЯ
Рассмотрим монокристаллический полупроводник у которого одна область легирована акцепторной примесью, а другая донорной (рис. 8.12).
Между электронной и дырочной областями кристалла существует тонкий переходной слой δ, который называется электронно-дырочным переходом или р-n переходом. Электронно-дырочный переход обладает резистивными, емкостными, выпрямительными свойствами, что позволяет его использовать в качестве основного структурного элемента большинства дискретных полупроводниковых приборов (диодов, транзисторов и др.) и интегральных микросхем.
По характеру распределения и соотношению концентраций донорных и акцепторных примесей в р- и n – областях р-n структуры различают резкие (рис. 8.13 а), плавные (рис. 8.13 в), симметричные (рис. 8.13 а) и несимметричные (рис. 8.13 б)
р-n переходы.
 |
Будем считать, что в р-n структуре создан несимметричный резкий р-n переход с распределением донорных и акцепторных примесей, представленном на рис. 8.14 б.
При комнатной температуре примесные атомы практически полностью ионизированы, поэтому в несимметричном резком р-n переходе (рис. 8.13 б) при NA >>ND из условия электрической нейтральности для р- и n- областей могут быть записаны равенства
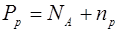, (8.11)
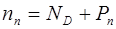, (8.12)
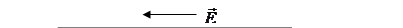Концентрации основных носителей заряда в р- и
n – областях в основном определяются концентрациями примесных атомов, поэтому равенства (8.11) и (8.12) можно записать в виде
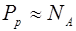, (8.13)
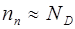. (8.14)
Концентрации неосновных носителей заряда могут быть найдены из закона действующих масс (7.23)
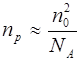, (8.15)
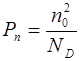. (8.16)
Из (8.15) и (8.16) следует, что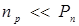 
(эффект подавления неосновных носителей).
Поскольку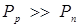 
и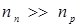 
, то на границе р- и
n- областей существует градиент концентрации электронов и дырок, вызывающий диффузионный ток дырок из р- области в n- область и электронов из
n- области в р- область. Диффузионный ток основных носителей нарушает электронейтральность областей кристалла, прилегающих к сечению х = 0, в котором изменяется тип примесей (рис. 8.14 б).
Это сечение называется металлургическим переходом. Сечение, в котором выравниваются концентрации электронов и дырок (n = P = n0 = P0), называется физическим переходом (сечение, проходящее через точку 1 на рис. 8.14 б).
В р – области, в слое толщиной δp, остается нескомпенсированный отрицательный заряд ионов акцепторной примеси, а в n- области, в слое толщиной δn, остается нескомпенсированный положительный заряд ионов донорной примеси (рис. 8.14 в). В результате в р-n переходе создается электрическое поле, направленное от n- области к p- области (рис. 8.14 а), которое вызовет дрейфовый ток неосновных носителей заряда. В отсутствии внешнего электрического поля в переходе устанавливается динамическое равновесие между встречными диффузионными и дрейфовыми токами электронов и дырок.
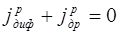, (8.17)
. (8.18)
Рассмотренные процессы приводят к возникновению в р-n переходе контактной разности потенциалов Uk
Для расчета Uk подставим в условие (8.17) плотности дрейфового (7.56) и диффузионного (7.61) токов.
С учетом известного соотношения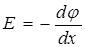 
получим дифференциальное уравнение
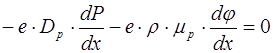(8.19)
Используем соотношение Эйнштейна (7.70), тогда уравнение (8.19) можно записать в виде
(8.20)
Проинтегрируем это уравнение в пределах р-n перехода, используя граничные условия: в р- области φ = φp, P = Pp, в n- области φ = φn, P = Pn. Поэтому, можем записать
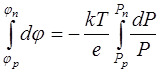
Выполняя интегрирование, получим
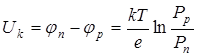. (8.21)
С учетом выражений (8.13) и (8.16) для Pp и Pn контактная разность потенциалов равна
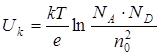. (8.22)
Из формулы (8.22) следует, что возникающий в р-n переходе потенциальный барьер eUk тем выше, чем больше концентрация примесей в р- и n – областях. Контактная разность потенциалов определяет сдвиг энергетических уровней в контактирующих р- и n- областях (рис. 8.15).
На рис. 8.15 а представлены энергетические диаграммы уединенных полупроводниковых кристаллов р- и n- типов. При образовании р-n структуры за счет динамического равновесия процессов диффузии и дрейфа носителей заряда в р-n переходе возникает потенциальный барьер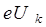 
, вызывающий взаимное смещение однотипных энергетических зон, как это показано на рис. 8.15 б. На рисунке 8.15 видно, что в условиях равновесия устанавливается единый уровень Ферми, а энергетический барьер имеет высоту:
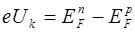. (8.23)
В области перехода энергетические уровни валентной зоны и зоны проводимости расположены наклонно, что связано с существованием электрического поля, которое выталкивает подвижные носители заряда за пределы перехода. По этой причине концентрация электронов и дырок в р-n переходе очень низкая.
Найдем характер изменения концентрации подвижных носителей заряда в
р-n переходе. Для этого проинтегрируем уравнение (8.20).
В р- области потенциал равен φр, а концентрация дырок равна РР. Для произвольной точки справа от границы раздела р- области и р-n перехода обозначим потенциал φ, а концентрацию дырок Р, тогда
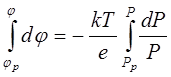(8.24)
Выполнив интегрирование, получим уравнение
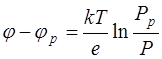(8.25)
откуда находим для Р выражение
. (8.26)
Из выражения (8.26) следует, что при смещении из р- области вглубь р-n перехода концентрация дырок экспоненциально уменьшается (рис. 8.14 б).
Проводя аналогичные расчеты, можно получить выражение для концентрации электронов при смещении из n- области вглубь р-n перехода:
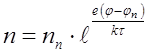(8.27)
График, описывающий изменение концентрации электронов представлен на
рис. 8. 14 б.
Из выражений (8.26) и (8.27) следует, что концентрация подвижных носителей в р-n переходе мала. По этой причине р-n переход является более высокоомной областью р-n структуры. Из-за вытеснения подвижных носителей заряда в р-n переходе существует нескомпенсированный заряд ионизированных атомов акцепторов и доноров. У границ перехода сказывается влияние дырок р- области и электронов
n- области (рис. 8.14 в). Суммарные заряды ионов доноров и акцепторов компенсируют друг друга в пределах р-n перехода и в целом он электрически нейтрален.
Рассчитаем изменение напряженности и потенциала электрического поля внутри р-n перехода.
Воспользуемся теоремой Гаусса-Остраградского для вектора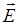 
в дифференциальной форме:
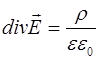, (8.28)
где ρ - объемная плотность заряда.
В одномерном случае уравнение (8.28) принимает вид
. (8.29)
Учтем, что в области нескомпенсированного отрицательного заряда ионов акцепторов (x < 0, на рис. 8.14 а)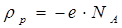 
и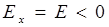 
, поэтому выполнив интегрирование в (8.29) получим:
. (8.30)
Постоянную интегрирования найдем, использовав граничное условие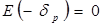 
:
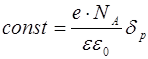. (8.31)
Таким образом, для области х < 0 находим
. (8.32)
В области нескомпенсированного положительного заряда доноров (x > 0, на
рис. 8.14 а)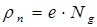 
и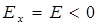 
, поэтому уравнение (8.29) принимает вид:
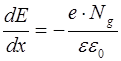. (8.33)
Выполнив интегрирование в уравнении (8.33) получим
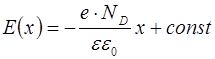. (8.34)
Постоянную интегрирования найдем, использовав граничное условие E (δn) = 0:
. (8.35)
Таким образом, для области x > 0 находим
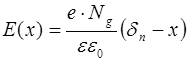. (8.36)
На рис. 8.14 д в соответствии с функциями (8.32) и (8.36) построен график изменения напряженности электрического поля внутри р-n перехода.
Для расчета изменения потенциала внутри р-n перехода воспользуемся известным соотношением
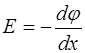. (8.37)
Для области x < 0 (рис. 8.14 а) Ex =E < 0, поэтому соотношение (8.37) должно быть записано в виде
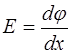. (8.38)
Выполнив интегрирование в (8.38), получим:
.
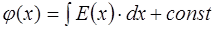Подставим в эту функцию E(x) из формулы (8.32) и используем граничное условие 
, тогда получим
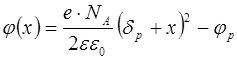(8.39)
В области x > 0 (рис. 8.14 а ) Ex =E < 0, поэтому интегрируем уравнение (8.38), подставив в него функцию E(x) из формулы (8.36):
,
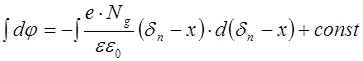откуда
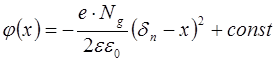. (8.40)
Постоянную интегрирования найдем, использовав граничное условие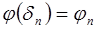 
:
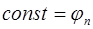. (8.41)
Таким образом, для области x > 0 получаем
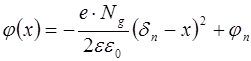. (8.42)
На рис. 8.14 г в соответствии с функциями (8.39) и (8.42) построен график изменения потенциала внутри р-n перехода.
Оценим толщину р-n перехода. Исключив влияние подвижных зарядов на нескомпенсированный заряд ионов примесных атомов, условие электрической нейтральности р-n перехода можно записать в виде:
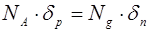. (8.43)
Толщину р-n перехода с использованием равенства (8.43) можно представить следующим выражением
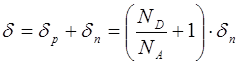(8.44)
Для резкого несимметричного р-n перехода при условии NA >> ND из выражения (8.41) следует, что весь переход окажется смещенным в n – область.
Выражение (8.39) и (8.42) при значении x = 0 должны быть равны друг другу, откуда следует равенство
. (8.45)
Из равенства (8.45), учитывая что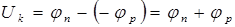 
(рис. 8.14 г) получаем выражение
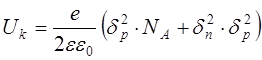. (8.46)
Преобразуем выражение в скобках (8.46), учитывая формулу (8.44)
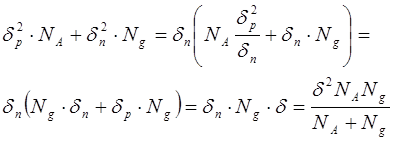(8.47)
Подставим выражение (8.47) в формулу (8.46), тогда получим
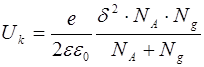
откуда, для толщины р-n перехода находим выражение
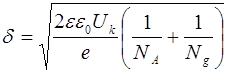. (8.48)
Для несимметричного р-n перехода (NA >> Ng) из формулы (8.48) следует, что
. (8.49)
Таким образом, толщина р-n перехода уменьшается с ростом концентрации примеси. Оценка толщины р-n перехода для реальных р-n структур дает значения от сотых долей до единиц микрометров.
Дата добавления: 2015-07-24; просмотров: 1001;