Закон сохранения энергии в механике. В механике есть силы, работа которых при перемещении тела по замкнутому контуру равняется нулю

В механике есть силы, работа которых при перемещении тела по замкнутому контуру равняется нулю. Такие силы называют­ся потенциальными, или консервативными.

Консервативной называется сила, работа которой при пере­мещении тела по замкнутому контуру равняется нулю.

Нетрудно показать, что консервативные силы обладают еще дву­мя свойствами:

1) работа консервативной силы при переходе тела из одного по­ложения в другое не зависит от траектории движения, а определя­ется только начальным и конечным положениями тела;

2) при изменении направления перехода работа консерватив­ной силы изменяет свой знак, не меняя величины Л, „ = —А₂—г

Опираясь на закон всемирного тяготения и закон Гука, можно доказать, что сила тяготения и упругая сила являются потенци­альными.

Потенциальность этих сил связана с тем, что на одном участке замкнутой траектории силы совершают положительную работу, а на другом — отрицательную так, что в сумме получается ноль. Покажем это на примере силы тяготения, действующей у поверх­ности Земли. Пусть тело проходит по замкнутой прямоугольной траектории 1—2—3—4—1 (рис. 9.1).

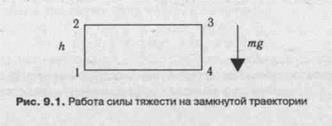
На участке 1—2 сила тяготения мешает движению, и ее рабо­та отрицательна: A_t_₂= —mgh. На участках 2—3 и 4—1 сила тяготения перпендикулярна направлению движения, и ее работа равна нулю: А₂_₃ = A_A__t = 0. На участке 3—4 сила тяготения помо­гает движению, и ее работа положительна: А₃__А = mgh. Полная работа на всем пути получается равной нулю:

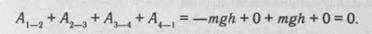
Не все силы являются потенциальными. Например, сила трения скольжения всегда направлена против движения тела и ее работа на всем пути — отрицательна. Сила трения не консервативна.

Работу консервативной силы удобно рассчитывать через умень­шение специальной величины — потенциальной энергии. Полу­чим соответствующую формулу.

Пусть тело переходит из положения 1 в положение 2 (рис. 9.2). Выберем некоторую точку пространства (О) в качестве точки отсчета и рассмотрим траекторию движения, проходящую через эту точку: 1—О—2.

Потенциальной энергией тела (£_п) называется скалярная вели­чина, равная работе, совершаемой консервативной силой, при пере­ходе тела из данного положения на выбранный уровень отсчета (О).

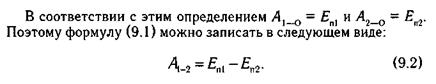
Таким образом, доказано, что работа консервативной силы рав­на убыли потенциальной энергии.