Свободные оси
Тело может вращаться не только вокруг закрепленной оси, но и вокруг оси, которая не закреплена. В любом теле можно выбрать такие оси, направление которых при вращении вокруг них будет сохраняться без каких либо специальных устройств (например, подшипников). Такие оси называют свободными.
Свободные оси — оси, которые без специального закрепления сохраняют свое направление в пространстве.
Пример: ось вращения Земли и волчка, ось всякого брошенного и свободно вращающегося тела.
Очевидно, что для однородных тел свободной осью является ось полной геометрической симметрии. Можно доказать, что в любом теле имеется не менее трех взаимно перпендикулярных свободных осей вращения, эти оси называются главными осями инерции. При этом оказывается, что при отсутствии внешних воздействий устойчивым является вращение тела только вокруг двух осей, относительно которых оно имеет наибольший или наименьший момент инерции. Например, если, подбросив тело, привести его во вращение
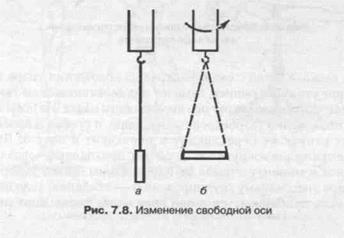
относительно произвольной оси, то, падая, оно само по себе перейдет к вращению вокруг оси, которой соответствует или наибольший, или наименьший момент инерции. В некоторых случаях, когда тело вращается около свободной оси с малым моментом инерции, оно самопроизвольно изменяет эту ось на ось с наибольшим моментом. На рис. 7.8 показана иллюстрация этого явления.
К электродвигателю подвешено на нити цилиндрическое тело, которое может вращаться вокруг своей вертикальной геометрической оси (а) с моментом инерции </, =——. При достаточно боль-шой угловой скорости тело изменит свое положение (б). Момент
1-2
инерции относительно новой оси равен J2 =—тг- • Если L2 > б/?2, то
/2 > /,. Вращение вокруг новой оси будет устойчивым.
Вращение человека в свободном полете и при различных прыжках происходит вокруг главной оси с наибольшим или наименьшим моментом инерции. Так как положение центра масс зависит от позы, то при различных позах направления главных осей будут различны.
У человека из-за наличия многозвенных, большей частью открытых в ходе движения кинематических цепей, имеется большое число степеней свободы. Так, подвижность кончиков пальцев относительно грудной клетки определяется 12 степенями свободы;
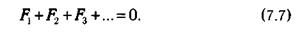
|
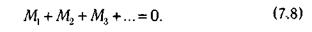
|
| сил тяжести. Для этого разобьем тело на множество маленьких кусочков и нарисуем действующие на них силы тяжести (рис. 7.10). |
запястья относительно лопатки — 7; а общее число степеней свободы всего тела — трехзначное число.
Пример
На рис. 7.9. представлена упрощенная модель скелета руки. Кинематическая схема показывает подвижные звенья скелета и типы шарнирных соединений (два шаровых шарнира и один цилиндрический). Эта модель имеет семь степеней свободы: три степени свободы в плечевом поясе, одна степень свободы в локтевом суставе и три степени свободы у кисти. На динамической схеме стрелками показаны оси вращения, соответствующие этим степеням свободы.
Дата добавления: 2015-07-24; просмотров: 1104;
