Глава 1. Свободные и вынужденные колебания
§ 1.1. Гармонический осциллятор
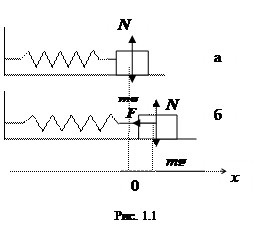 Рассмотрим груз, закрепленный на упругой пружине. Эта физическая система называется пружинным маятником, если груз можно считать материальной точкой, а пружину - невесомой и идеально упругой. При деформации пружины груз движется вдоль оси x, начало которой (х=0) совместим с положением равновесия груза (рис1.1 а). Растяжению пружины соответствует х>0, сжатию - х<0. Сместим груз из положения равновесия (рис.1.1.б), отпустим его и рассчитаем его дальнейшее движение. Для этого составим и решим уравнение движения. Для материальной точки таковым является уравнение второго закона Ньютона: ma=SF. Будем считать трение при движении груза пренебрежимо малыми. На груз действуют три силы: тяжести mg, реакция опоры N и сила упругости пружины F. Движение груза одномерное Проекции на ось x силы тяжести и реакции опоры равны нулю, силы упругости F= -kx, так что уравнение движения в проекции на ось x примет вид: ma = - kx. Учитывая, что a=d2x/dt2, получили md2x/dt2 = -kx, где m-масса и k-коэффициент жесткости - постоянные. Введем новую постоянную:
Рассмотрим груз, закрепленный на упругой пружине. Эта физическая система называется пружинным маятником, если груз можно считать материальной точкой, а пружину - невесомой и идеально упругой. При деформации пружины груз движется вдоль оси x, начало которой (х=0) совместим с положением равновесия груза (рис1.1 а). Растяжению пружины соответствует х>0, сжатию - х<0. Сместим груз из положения равновесия (рис.1.1.б), отпустим его и рассчитаем его дальнейшее движение. Для этого составим и решим уравнение движения. Для материальной точки таковым является уравнение второго закона Ньютона: ma=SF. Будем считать трение при движении груза пренебрежимо малыми. На груз действуют три силы: тяжести mg, реакция опоры N и сила упругости пружины F. Движение груза одномерное Проекции на ось x силы тяжести и реакции опоры равны нулю, силы упругости F= -kx, так что уравнение движения в проекции на ось x примет вид: ma = - kx. Учитывая, что a=d2x/dt2, получили md2x/dt2 = -kx, где m-масса и k-коэффициент жесткости - постоянные. Введем новую постоянную:
w2=k/m (1.1.1)
Уравнение движения примет вид дифференциального уравнения второго порядка с постоянными коэффициентами без правой части:
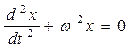 (1.1.2)
(1.1.2)
Из математики известно[1], что его решение имеет вид гармонической функции:
x=Asin(w t + j0)=Acos( wt+ j0’) (1.1.3)
где A, j0,j0’ - постоянные, зависящие от начальных условий, при этом j0 =j0’+p/2.
Выясним физический смысл полученного результата. Здесь х - координата, т.е. смещение груза из положения равновесия представляет собой знакопеременную величину. Почему? Упругая сила всегда направлена к положению равновесия и, казалось бы, должна вернуть груз в точку x=0. Однако по мере приближения к ней скорость груза растет, он по инерции минует эту точку, и его смещение меняет знак, увеличиваясь по модулю. Теперь направления упругой силы и скорости противоположны, так что движение замедляется, пока скорость не уменьшится до нуля. После этого груз, ускоряясь, начинает двигаться к положению равновесия, и рассмотренный процесс повторяется. Такое многократно повторяющееся изменение состояния физической системы называют колебаниями.
Колебания свойственны различным формам движения материи и хорошо знакомы нам. Примеры механических колебаний - движения маятников, шатунов, рессор, морские приливы и отливы, звук. Примеры электромагнитных колебаний - переменный электрический ток, процессы в колебательных контурах различных приемников и передатчиков электромагнитных средств связи, свет и т. д. По образному выражению крупного российского физика начала ХХ века Мандельштама в физике есть языки “национальные”- механики, акустики, оптики, электродинамики и есть “интернациональный” язык теории колебаний. Колебания любой физической природы описываются одинаковым математическим аппаратом, поэтому мы подробно рассмотрим только механические колебания и используем упомянутую аналогию при рассмотрении колебаний другой физической природы.
Общими для возникновения колебаний любой природы являются два условия. Первое состоит в том, что система имеет положение устойчивого равновесия. Это означает, что такому положению соответствует минимум потенциальной энергии системы, и что при отклонении от него возникает возвращающая сила F= -kx (в рассматриваемом случае это упругая сила), стремящаяся вернуть систему в равновесие. Второе условие - это инерционность системы, которая не позволяет ей остановиться в положении равновесия.
Колебания, которые совершает система, выведенная из положения равновесия и предоставленная самой себе, называются свободными. Если система колеблется под действием только внутренних сил (силами трения можно пренебречь), как в рассмотренном примере пружинного маятника, то ее колебания называются собственными.
Движение (процесс) называется периодическими, если каждое состояние системы повторяется через определенный промежуток времени. Его называют периодом - Т. Из этого определения следует:
x(t)=x(t+nT) (1.1.4)
где n-любое целое число. Другая характеристика периодических процессов - частота n равначислу колебаний в единицу времени. Следовательно,
n = 1/T (1.1.5)
Простейшим типом периодических колебаний являются гармонические, при которых изменение характеристик состояния системы происходит по гармоническому закону, т.е. по закону синуса или косинуса (1.1.3). Этот тип колебаний часто встречается в природе и в технике, он наиболее прост с точки зрения математического описания и, что особенно важно, периодический процесс любого вида (и даже не периодический) может быть представлен как сумма конечного или бесконечного числа гармонических колебаний с разными частотами. В математике такому гармоническому анализу соответствует разложение в ряд Фурье, в физике - разложение в спектр. Спектральный анализ широко применяется в науке и в технике. Таким образом, изучение гармонических колебаний открывает широкие возможности анализа и понимания различных физических процессов.
Система, совершающая колебания, называется осциллятором (от латинского oscillare -колебаться). Закон движения гармонического осциллятора выберем в виде (см.формулу 1.1.3):
x =A sin(wt+j0) (1.1.6)
и вспомним известный из школы смысл входящих в него величин.
x - смещение, т.е. отклонение колеблющейся величины от положения равновесия, принятого за начало отсчета.
A - амплитуда, т.е. максимальное смещение, A=const. В нашем примере (рис.1) амплитуда равна начальному смещению груза из положения равновесия, т.е. величину амплитуды задает сообщенная системе энергия колебаний,
j=(wt+j0) - фаза колебаний, аргумент гармонической функции, в СИ измеряется в радианах j0 - значение фазы при t=0 называют начальной фазой. Фаза определяет состояние системы в каждый момент времени и является линейной функцией времени. Если два колебания имеют разные фазы, то говорят, что они сдвинуты по фазе. При сдвиге по фазе на p говорят, что колебания происходят в противофазе. Колебания с одинаковыми фазами или с разностью фаз, кратной 2p, называют синфазными.
w - круговая или циклическая частота, в СИ измеряется в рад/с. Из формулы (1.1.2) видно, что частота определяется параметрами колебательной системы: упругостью и массой маятника и не зависит от величины начального смещения. Используя соотношения (1.1.4) и (1.1.5), самостоятельно убедитесь в том, что
w =2p/T=2pn (1.1.7)
Таким образом, круговая (циклическая) частота равна числу колебаний за 2p единиц времени и является аналогом угловой скорости при вращательном движении, если под T понимать период вращения.

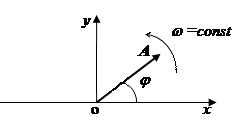 Аналогию между колебательным и вращательным движениями можно продолжить, рассматривая фазу колебаний как угол поворота и изображая гармоническое колебание вектором (рис.1.2). Пусть вектор, модуль которого равен амплитуде колебаний A, равномерно вращается в плоскости xy вокруг неподвижного центра O с постоянной угловой скоростью w. Уголj, образованный им с осью диаграммы, равен фазе колебаний. Проекции вектора на оси диаграммы x и y изменяются по гармоническому закону, причем закону в форме (1.1.6) соответствует проекция на ось y.
Аналогию между колебательным и вращательным движениями можно продолжить, рассматривая фазу колебаний как угол поворота и изображая гармоническое колебание вектором (рис.1.2). Пусть вектор, модуль которого равен амплитуде колебаний A, равномерно вращается в плоскости xy вокруг неподвижного центра O с постоянной угловой скоростью w. Уголj, образованный им с осью диаграммы, равен фазе колебаний. Проекции вектора на оси диаграммы x и y изменяются по гармоническому закону, причем закону в форме (1.1.6) соответствует проекция на ось y.
Вернемся к рассмотрению пружинного маятника. Как следует из формул (1.1.1) и (1.1.7), его период колебаний:
T=2p 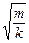 (1.1.8)
(1.1.8)
В рассматриваемом нами примере пружинного маятника его движение задано внутренними силами, поэтому формулы (1.1.7) и (1.1.8) выражают соответственно круговую частоту и период собственных колебаний. Обратите внимание, что они заданы собственными параметрами колебательной системы - m и k и не зависят от начальных условий, в частности, от амплитуды колебаний. Чем больше инертность (масса) маятника, тем медленнее изменяется его движение. С другой стороны, чем больше жесткость пружины, тем быстрее реагирует груз на ее воздействие.
Проанализируем другие характеристики колебательного гармонического движения, используя известные из механики соотношения u=dx/dt, a=du/dt, F=ma. Помимо смещения -x гармонически изменяются скорость - u, ускорение - a, возвращающая сила - F, причем, все они колеблются с одинаковыми частотами. Убедитесь в этом самостоятельно, а также в том, что соответствующие амплитуды равны:
umax =Av, amax=Av2, Fmax=mav2 (1.1.9)
и что сдвиг по фазе между скоростью и смещением составляет p/2, ускорение и смещение колеблются в противофазе, а колебания возвращающей силы и ускорения синфазны.
Для возбуждения колебаний систему надо вывести из положения равновесия, т.е. сообщить ей дополнительную энергию. Возвращающая сила F= -kx создает потенциальную энергию:
Wп = kx2/2 = (kA2/2) sin2(wt+j0 ) (1.1.10)
Движущееся тело обладает энергией кинетической
Wк =mu2/2 = (mA2v2/2) cos2(vt+j0).(1.1.11)
Значения потенциальной и кинетической энергий при колебаниях изменяются, при этом полная механическая энергия сохраняется:
W=Wк+Wп = kA2/2 = mA2/2 (1.1.12)
Это закономерно, так как колебания осциллятора происходят под действием консервативной силы. Проанализируйте самостоятельно, в каких состояниях осциллятор имеет только потенциальную энергию, а в каких только кинетическую, и как происходят взаимные превращения этих видов энергии друг в друга.
Подведем итоги:
1. Система, уравнение движения которой имеет вид
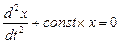 (1.1.13)
(1.1.13)
является гармоническим осциллятором, совершающим колебания с круговой частотой w= 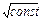 .
.
2. Частота собственных колебаний определяется параметрами колебательной системы и не зависит от внешних условий, в частности, от запаса энергии, сообщенной осциллятору при возбуждении колебаний .
3. При гармонических колебаниях механического осциллятора гармонически колеблются смещение, скорость, ускорение, возвращающая сила, причем, частоты их колебаний совпадают, а амплитуды и фазы колебаний разных характеристик движения согласованы; кинетическая и потенциальная энергии колеблются с удвоенной частотой в противофазе, тогда как полная энергия сохраняется.
§ 1.2.Примеры гармонических осцилляторов.
Реальные физические системы при малых отклонениях от положения равновесия можно считать гармоническими осцилляторами, если силы сопротивления малы. Рассмотрим такие системы.
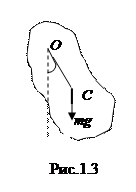 1) Физический маятник
1) Физический маятник
Тело, подвешенное на горизонтальной оси, не проходящей через его центр тяжести, и выведенное из положения равновесия, качается под действием силы тяжести mg.. Такое твердое тело и есть физический маятник (рис.1.3) Неподвижная горизонтальная ось перпендикулярна плоскости рисунка и проходит через точку O. Центр тяжести тела – точка C. Расстояние OC обозначим b. Составим уравнение движения этого тела, для чего используем основной закон динамики вращательного движения: Ie = SM, где I - момент инерции тела относительно оси O, e - угловое ускорение, e=d2a/dt2, где a - угол отклонения прямой OC от вертикали, M - момент силы относительно оси O. На тело действует сила тяжести mg, приложенная в центре тяжести C, и сила реакции опоры, приложенная в точке O. В положении равновесия эти силы направлены вдоль прямой OC в противоположные стороны и уравновешивают друг друга, если тело покоится. При отклонении тела на угол a сила тяжести создает момент M = - mgb sina..Знак “ минус “ обусловлен противоположными направлениями векторовda иM. Пренебрегая трением в подвесе и сопротивлением воздуха, получим:
d2a /dt2 = - mgbsina (1.2.1)
Для малых углов sina»a, так что уравнение движения примет вид:
d2a/dt2 + (mgb/I)a = 0 (1.2.2)
Сравнивая (9.1.13) и (9.2.2), видим, что малые колебания физического маятника являются гармоническими с периодом
T=2p 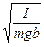 (1.2.3)
(1.2.3)
Примерами физических маятников могут служить маятники часов, раскачиваемые ветром линии электропередач, здания, поднимаемые грузы, перевозимые в цистернах жидкости и т. п.
2) Математический маятник -маленький груз (материальная точка) массы m , подвешенный на невесомой нерастяжимой нити длиной l. Он является частным случаем физического маятника с моментом инерции I =ml2 и расстоянием от точки подвеса до центра тяжести b=l, так что
T = 2p 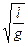 (1.2.4)
(1.2.4)
Формулу (1.2.4) используют для определения с высокой точностью ускорения свободного падения g, зависящего от плотности залегающих в земле пород, и применяют в геологоразведке.
Физический маятник характеризуют приведенной длиной L. Она равна длине математического маятника, колеблющегося с тем же периодом, что и физический. Из сравнения формул (1.2.3) и (1.2.4) следует: L= I/mb.
Роль возвращающей силы при колебаниях физического и математического маятников играет составляющая силы тяжести, которая является консервативной, поэтому полная механическая энергия колебаний сохраняется.
3) Колебательный контур.
Убедимся в том, что процессы, происходящие в гармонических осцилляторах любой 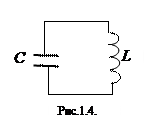 физической природы, подчиняются одинаковым закономерностям.
физической природы, подчиняются одинаковым закономерностям.
Рассмотрим замкнутую электрическую цепь, состоящую из конденсатора емкостью C и катушки с индуктивностью L (рис.1.4). Равновесие в такой цепи означает электрическую нейтральность всех ее участков. При отклонении от равновесия происходит смещение положительных зарядов относительно отрицательных. Этого можно достичь, зарядив конденсатор, т.е. переместив некоторое количество свободных электронов с одной пластины на другую. Для этого достаточно присоединить конденсатор к источнику постоянного тока, при этом на одной пластине тут же появится избыточный положительный заряд, а на другой - такой же по модулю отрицательный заряд. Возникшее электрическое поле будет работать как возвращающая сила. Отключение источника тока и соединение обкладок конденсатора друг с другом через катушку индуктивности создаст второе условие возникновения колебаний - инерционность системы: ток в катушке не может сразу прекратиться вследствие явления самоиндукции.
Составим уравнение движения заряда. Уравнением движения для электрической цепи является закон Ома или, что то же самое, второе правило Кирхгофа. Согласно ему, сумма падений напряжений на всех участках замкнутого контура равна сумме ЭДС, действующих в этом контуре. Напряжение U на конденсаторе и его заряд q связаны между собой соотношением U=q/C. Катушка при протекании по ней изменяющегося тока становится источником тока с ЭДС ε = - L di/dt . Таким образом, уравнение движения для рассматриваемой колебательной системы примет вид:
q/C = - L di/dt (1.2.5)
Учитывая, что i=dq/dt, получим уже знакомое нам уравнение гармонического осциллятора:
d2q/dt2 + (1/LC)q=0 (1.2.6)
Его решение имеет вид:
q=qm cos(wt+j0) (1.2.7)
где
w = 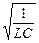 (1.2.8)
(1.2.8)
При этом напряжение на конденсаторе колеблется синфазно с зарядом:
U=(qm/C)cos(wt+j0) (1.2.9)
а ток опережает по фазе напряжение на p/2:
i=qmw sin(wt+j0) (1.2.10)
Энергия электрического поля в конденсаторе
Wэ=q2/(2C)=(qm2/2C)cos2(wt+j0) (1.2.11)
и энергия магнитного поля в катушке
Wм= Li2/2 = Lqm2w 2sin2(wt+j0) (1.2.12)
со временем изменяются подобно потенциальной и кинетической энергиям при механических колебаниях, тогда как полная энергия колебаний сохраняется:
W =Wэ+Wм=qм 2/2С=Lqм 2w 2/2 (1.2.13)
Таким образом, колебания в контуре по своей природе являются электромагнитными и происходят с периодом, выражаемым известной из школы формулой Томсона:
T = 2p 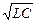 (1.2.14)
(1.2.14)
В современной технике электромагнитные колебания играют значительно большую роль, нежели механические, так как лежат в основе устройств связи, телевидения, радиолокации, энергетики, всевозможных электронных и электромагнитных приборов.
§ 1.3. Затухающие колебания
Опыт показывает, что свободные колебания реальных физических систем затухают, так как первоначальный запас энергии колебаний расходуется на преодоление сопротивления и превращается в теплоту, излучение и т.д. Количественной характеристикой затухания служит добротность колебательной системы - Q, равная отношению энергии колебаний W к ее потерям DW[2]:
Q=W/DW (1.3.1)
Из определения следует, чем больше добротность, тем медленнее затухают колебания, и тем ближе колебательная система к идеальной. Добротность гармонического осциллятора равна бесконечности.
Рассмотрим свободные колебания пружинного маятника и учтем тормозящее действие на него окружающей среды (например, воздуха). Помимо возвращающей силы Fвозвр=-kx действует сила вязкого трения Fтр=-ru, где r - постоянный коэффициент, зависящий от размеров и формы тела, а также от вязкости среды, u - скорость тела.. Запишем уравнение движения : md2x/dt2=-kx-ru. Учитывая, что u=dx/dt, и введя новые обозначения постоянных коэффициентов 2b =r/m и w02=k/m. (их физический смысл выясним чуть позже), получаем линейное дифференциальное уравнение второго порядка с постоянными коэффициентами и без правой части:
d2x/dt2+2bdx/dt+w02x=0. (1.3.2)
Из математики известно, что его решение имеет вид;
x=C1 exp(l1t)+C2 exp(l2t), (1.3.3)
где С1 и C2 - постоянные, l1 и l2 - корни характеристического уравнения l2+2bl+w02=0, равные 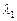 l1,2=-b ±
l1,2=-b ± 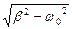 .
.
Проанализируем физический смысл полученного результата. Если силы трения малы, т.е.
b 2-w02 <0, то закон движения (1.3.3) удобно записать в виде:
x=A0 exp(-b t)sin(w t+j0), (1.3.4)
где A0 и j0 - постоянные, определяемые начальными условиями, т.е. начальным смещением - x0 и начальной скоростью - υ0при t=0. На рис.1.5 этот закон движения представлен графиком. Это колебание не является гармоническим, так как размах колебаний уменьшается, поэтому понятия “частота”, “период”, “амплитуда” к нему можно применять условно. Промежуток времени между двумя последовательными максимальными отклонениями маятника от положения равновесия в одну и ту же сторону называют периодом колебаний Т. Циклическая частота
 w =(w02 - b 2)1/2 (1.3.5)
w =(w02 - b 2)1/2 (1.3.5) 
Она тем меньше, а период колебаний T=2p/w тем больше, чем больше b. Коэффициент перед синусом в законе движения называют амплитудой затухающих колебаний:
A=A0 e- b t (1.3.6)
На графике она изображена тонкой линией, огибающей максимальные смещения маятника от положения равновесия. Чем больше коэффициент b, т.е чем больше трение, тем быстрее затухают колебания. Коэффициент b называют коэффициентом затухания. Обратите внимание, что b t- есть показатель степени, безразмерная величина, так что коэффициент затухания измеряют в СИ в с-1. Таким образом, трение тормозит движение колебательной системы, увеличивая период колебаний и уменьшая их размах. В идеальной колебательной системе без трения (b=0) частота свободных колебаний w=w0 и определяется только свойствами самой колебательной системы (упругостью и массой маятника), поэтому w0 называется собственной циклической частотой.
В качестве количественной характеристики скорости затухания колебаний используют декремент затухания, равный отношению амплитуд двух следующих друг за другом колебаний: A(t)/A(t+T). Логарифм этого отношения называют логарифмическим декрементом затухания:
Q=lnA(t)/A(t+T)=bT (1.3.7)
Выясним его физический смысл. Промежуток времени t, в течение которого амплитуда уменьшается в е=2,7 раз, называют временем жизни (или временем релаксации) колебаний. Из формулы (1.3.6) следует, что
t=1/b (1.3.8)
За время t система совершает Nе колебаний. Используя (1.3.7) и (1.3.8), получим:
Ne=t/T=tb/Q=1/Q (1.3.9)
Таким образом, логарифмический декремент затухания равен обратному числу колебаний, уменьшающему амплитуду в е раз. Естественно, что логарифмический декремент затухания связан с добротностью Q:
Q=p/Q=pNe (1.3.10)
Если силы трения велики (т.е. b 2-w02³ 0), то при b®w0, как следует из формулы (1.3.5), w ® 0, следовательно, T® ¥. Это означает, что система, будучи выведена из положения равновесия, плавно возвращается к нему. Такой процесс называется апериодическим (т.е. непериодическим). Попробуйте самостоятельно нарисовать два примера апериодических законов движения: мысленно поместите пружинный маятник в очень вязкую среду, отклоните его от положения равновесия и толкните его в первом примере к положению равновесия, а во втором примере в противоположную сторону. Как разные начальные условия отразятся на этих графиках?
Свободные колебания часто встречаются в технике. Если колебания должны поддерживаться длительное время, то затухание вредно и с ним нужно бороться, уменьшая трение. В таких случаях в механических устройствах применяют смазку, подшипники и т.п. Например, в механических часах опоры осей делают конической формы из твердых камней (агат, рубин). Если колебания нежелательны, их стремятся погасить, увеличивая трение с помощью успокоителей (демпферов). Подобные устройства используются в звеньях механических машин, гидравлических устройствах, электроизмерительных приборах.
Нередко к наличию колебаний следует подходить диалектически. Гасить их чрезмерной жесткостью опасно, так как это приводит к ударам, разрушающим здания, перевозимые грузы, станки, стрелки измерительных приборов. Подобные удары амортизируют упругими подвесками, растяжками: сейсмическую стойкость зданий обеспечивают мощной упругой “подушкой“; столы для чувствительных измерений, кузова автомобилей, перевозимые хрупкие предметы крепят на упругих подвесках.
Подведем итоги:
1.Уравнение движения свободных механических колебаний в присутствии сил вязкого трения имеет вид: d2x/dt2+2b dx/dt+w02x=0, где b - коэффициент затухания,w0 - собственная циклическая частота.
2.Характер закона движения определяется величиной трения. Если трение мало (математически это выражается так: b <<w0), то колебания похожи на гармонические, однако их амплитуда экспоненциально уменьшается со временем; и такие колебания называются затухающими. Быстрота затухания (диссипации энергии) характеризуется логарифмическим декрементом затухания, временем жизни колебаний, добротностью колебательной системы. Эти характеристики взаимосвязаны между собой. Если трение велико (b ³w0 ), то движение становится апериодическим.
3.Закономерности свободных колебаний, установленные нами для механического движения, справедливы для колебаний любой физической природы, в частности, для электромагнитных колебаний в электрическом колебательном контуре, имеющем сопротивление.
§1.4. Вынужденные колебания. Резонанс.
Для поддержания колебаний необходимо компенсировать потери колебательной энергии с помощью какого-либо внешнего источника. Очевидно, что внешняя сила, поддерживающая колебания, не может быть постоянной или действовать однократно. Она должна быть периодической. В простейшем случае это может быть гармонически изменяющаяся сила:
F=F0 sinwt. Такую силу называют вынуждающей, а колебания под действием вынуждающей силы - вынужденными. В уравнении движения помимо возвращающей силы и силы трения появится еще вынуждающая сила:
md2x/dt2=-kx-rv+Fo sinwt. (1.4.1)
Используя обозначения, введенные в уравнении (9.3.2), получим:
d2x/dt2+2b dx/dt+w02x =(F0/m)sinwt. (1.4.2)
Это уравнение отличается от (1.3.2) только наличием правой части, т.е. является неоднородным. Из математики известно, что его решение есть сумма двух решений: общего решения соответствующего однородного уравнения (это затухающие колебания) и частного решения уравнения (1.4.2). По прошествии некоторого времени вследствие затухания первое слагаемое обратится в ноль и в установившемся режиме движение описывается только вторым слагаемым - частным решением. Найдем его. Из опыта понятно, что под действием периодической силы система будет колебаться с частотой этой силы. Поэтому решение уравнения (1.43) логично предположить в виде:
x=Asin(wt+j). (1.4.3)
A и j - постоянные, соответственно амплитуда и начальная фаза, значения которых надо определить. Для этого подставим (1.4.3) в (1.4.2) .В результате получим:
A(w02-w2)sin(wt+j)+2Abw cos(wt+j)=(F0/m)sinwt (1.4.4)
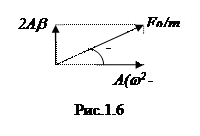 Потребуем, чтобы последнее уравнение обратилось в тождество. Для этого воспользуемся методом векторных диаграмм. В левой части (1.4.4) складываются два гармонических колебания с одинаковыми частотами и отличающимися на p/2 начальными фазами. Их можно изобразить взаимно перпендикулярными векторами и сложив, получить вектор, соответствующий правой части (1.4.4), что представлено на рис.1.6. Используя простые математические преобразования, получим:
Потребуем, чтобы последнее уравнение обратилось в тождество. Для этого воспользуемся методом векторных диаграмм. В левой части (1.4.4) складываются два гармонических колебания с одинаковыми частотами и отличающимися на p/2 начальными фазами. Их можно изобразить взаимно перпендикулярными векторами и сложив, получить вектор, соответствующий правой части (1.4.4), что представлено на рис.1.6. Используя простые математические преобразования, получим:
A=(F/m)/ 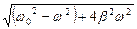 (1.4.5)
(1.4.5)
tgj=-2bw /(w02-w2) (1.4.6)
Из этих формул следует, что амплитуда и начальная фаза вынужденных колебаний не зависят от начальных условий, а определяются только параметрами колебательной системы и возвращающей силы. Это закономерно, так как мы рассматриваем установившийся режим, когда свободные колебания уже “затухли” и система “забыла” свое начальное состояние.
Рассмотрим, как влияет частота вынуждающей силы w на величину амплитуды A. Из формулы (1.4.5) следует, что при w=0 (постоянная сила) система сместилась на расстояние x0=A=F0/(mw02)=F0/k и вновь уравновесилась. Если w®¥, то A®0. Это означает, что вследствие инерционности система не успевает реагировать на слишком часто изменяющееся направление внешнего воздействия и остается на месте. При некотором значении частоты вынуждающей силы амплитуда резко возрастает и достигает максимума. Это явление называется резонансом, а соответствующая частота - резонансной частотой wр. Очевидно, что резонансная частота соответствует минимуму подкоренного выражения в формуле (1.4.5). Дифференцируя его и приравнивая результат к нулю (т.е. проведя исследование функции на экстремум), получим:
wр= 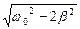 . (1.4.7)
. (1.4.7)
Проанализируем полученную формулу: трение препятствует движению, замедляет его, увеличивая период и уменьшая резонансную частоту по сравнению с частотой собственных колебаний. Если трение мало (b<<w0), то резонансная частота практически совпадает с собственной частотой.
Подставим в формулу (1.4.5) формулу (1.4.7), найдем резонансную амплитуду:
Ар = 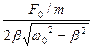 (1.4.8)
(1.4.8)
В частности, при b<<w0
Ар » 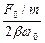 (1.4.9)
(1.4.9)
А если b®0, то Ар®¥. Существует правило: солдаты строем по мосту не ходят. Оно делается вполне понятным, если вспомнить про резонанс.
С энергетической точки зрения резонанс представляет собой способность колебательной системы активно поглощать энергию, сообщаемую ему источником колебания. Резонанс – это максимально благоприятный отклик колебательной системы на внешнее воздействие. Анализируя способность студентов усваивать учебный материал, можно сказать, что ближе к концу семестра возникает резонанс: студенты на лету схватывают сообщаемую им преподавателями учебную информацию.
[1] Если Вы не знакомы с решением дифференциальных уравнений, то, исходя из опыта, «угадаем» решение этого уравнения. Очевидно, оно будет выражаться формулой (1.1.3). Проверим свою догадку, для чего подставим (1.1.3) в (1.1.2) и убедимся в своей правоте.
[2] Рассматривается отношение средней энергии и средних ее потерь за четверть периода, т.е. минимальный промежуток времени, за который проявляются все характерные признаки данного колебания, а именно, один вид энергии полностью переходит в другой вид.
| <== предыдущая лекция | | | следующая лекция ==> |
| Поляризация световых волн | | | Призначення та особливості електронних таблиць |
Дата добавления: 2015-08-08; просмотров: 1419;
